LeetCode 1825 求出MK平均值【Set 队列】 HERODING的LeetCode之路

解题思路：
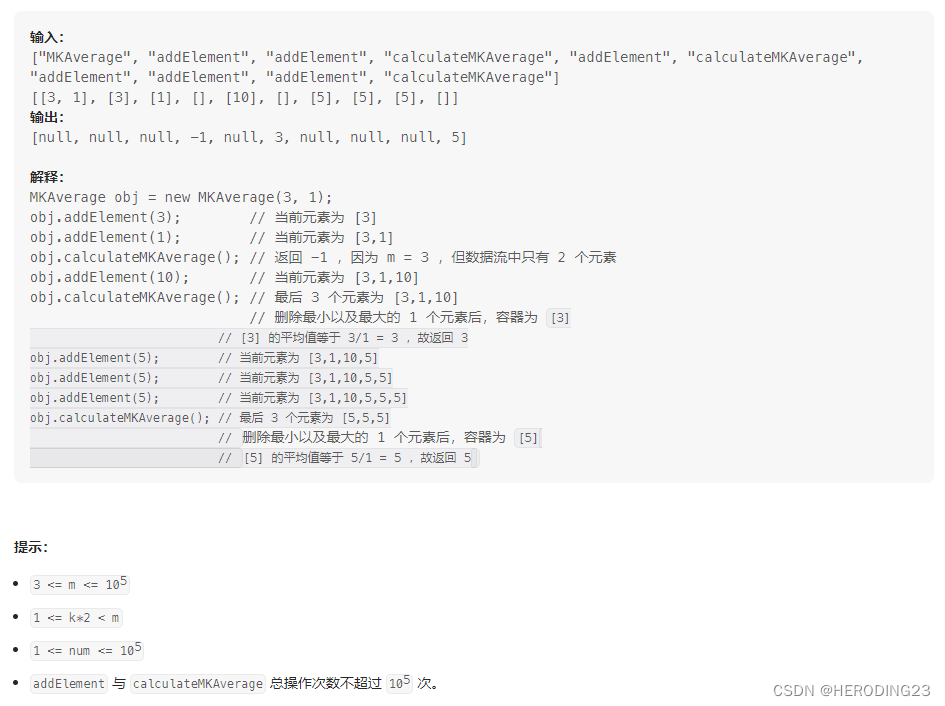
好久没更新力扣困难题的题解了，今天这道困难题有点意思，读罢题目一目了然，解题思路清晰明了，就是解题过程细节满满。这是一个数据流场景的问题，保留最后m个元素，但是要去除k个最大，k个最小，返回平均值。这时候数据结构一目了然，那就用三个集合存储k小，k大和m-2k呗，那数据流最后m个如何保证呢，队列！用队列存储序列，当队列的长度超出m，队首出列，同时在三个集合中寻找并删除相关数。那么解题过程如下：

1. 定义三个集合，一个队列，以及变量sum存储m-2k队列的求和；
2. 构造函数初始化m，k；
3. addElement中，首先元素入队列；
4. 如果数据没满， 数据流入s2中；
5. 满了，s2中的元素k小进入s1，k大进入s2；
6. 如果数据超出m，要想办法把超的数放入s2中；
7. num比k小集合最大的小，把k小集合中最大的放入s2中；
8. num比k大集合最小的大，把k大集合中最小的放入s2中；
9. 开始删减，temp为队列中第一个元素；
10. 先在s1中寻找，再s3和s2，找到temp即删除；
11. calculateMKAverage函数中，不足m返回-1，否则返回sum / (m - 2 * k)；

其中第6步骤非常巧妙，因为数据流中的元素重复，在删除阶段可能会把后来的相同的数删除，那么我们只要保证后来的相同的数在s2中，最后才删s2，这就保证了先来的相同的元素一定会在s1或者s3中先删除，即使s2中有多个重复也不影响最终结果（但是在s1或s3中会影响）。代码如下：

class MKAverage {
private:
    int m, k;
    // 三个集合，分别存储k小、m-2k、k大
    multiset<int> s1, s2, s3;
    queue<int> q;
    long long sum;
public:
    MKAverage(int m, int k) {
        this -> m = m;
        this -> k = k;
        sum = 0;
    }
    
    void addElement(int num) {
        q.push(num);
        // 如果数据流没满
        if(q.size() <= m) {
            s2.insert(num);
            sum += num;
            // 数据流刚好满了
            if(q.size() == m) {
                // 最小集合没满
                while(s1.size() < k) {
                    s1.insert(*s2.begin());
                    sum -= *s2.begin();
                    s2.erase(s2.begin());
                }
                // 最大集合没满
                while(s3.size() < k) {
                    s3.insert(*s2.rbegin());
                    sum -= *s2.rbegin();
                    s2.erase(prev(s2.end()));
                }
            }
            return;
        }
        // 数据流超出
        // 比k小集合最大的小
        if(num < *s1.rbegin()) {
            s1.insert(num);
            s2.insert(*s1.rbegin());
            sum += *s1.rbegin();
            s1.erase(prev(s1.end()));
        } else if(num > *s3.begin()) {
            // 比k大集合最小的大
            s3.insert(num);
            s2.insert(*s3.begin());
            sum += *s3.begin();
            s3.erase(s3.begin()); 
        } else {
            s2.insert(num);
            sum += num;
        }

        // 由于数据流超出1，删减
        int temp = q.front();
        q.pop();
        // 如果在k小集合
        if(s1.count(temp)) {
            s1.erase(s1.find(temp));
            s1.insert(*s2.begin());
            sum -= *s2.begin();
            s2.erase(s2.begin());
        } else if(s3.count(temp)) {
            // 如果在k大集合
            s3.erase(s3.find(temp));
            s3.insert(*s2.rbegin());
            sum -= *s2.rbegin();
            s2.erase(prev(s2.end())); 
        } else {
            // 在m-2k集合中
            s2.erase(s2.find(temp));
            sum -= temp;
        }

    }
    
    int calculateMKAverage() {
        if(q.size() < m) {
            return -1;
        } 
        return sum / (m - 2 * k);
    }
};

/**
 * Your MKAverage object will be instantiated and called as such:
 * MKAverage* obj = new MKAverage(m, k);
 * obj->addElement(num);
 * int param_2 = obj->calculateMKAverage();
 */