蒙特卡洛算法
近似估算 π \pi π值
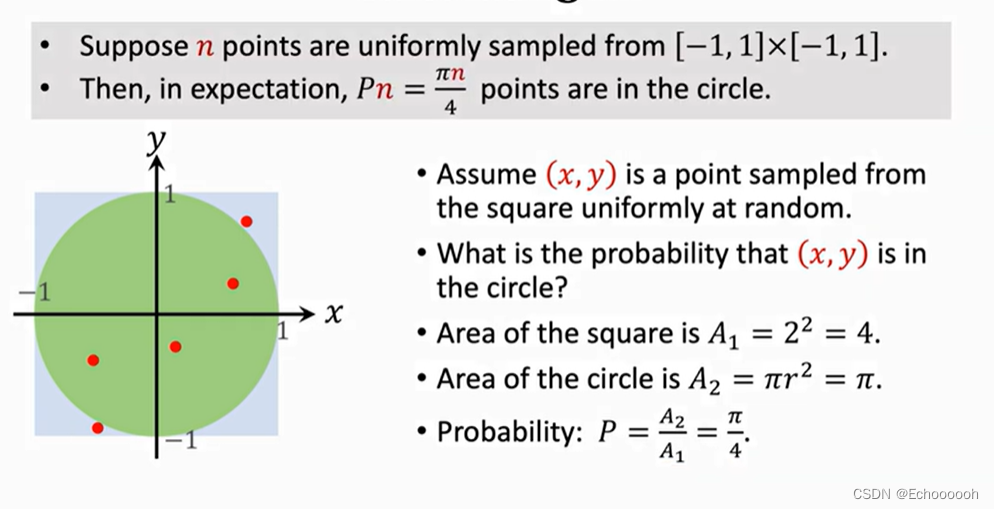
如何判断点是否在圆里面?:
x
2
+
y
2
≤
1
x^2+y^2\leq1
x2+y2≤1
当抽的次数非常多的时候(n非常大),在圆里面的点的数量m,
m
≈
π
n
4
m\approx \frac{\pi n}{4}
m≈4πn(实际观测值
≈
\approx
≈期望)
得到
π
≈
4
m
n
\pi \approx \frac{4m}{n}
π≈n4m
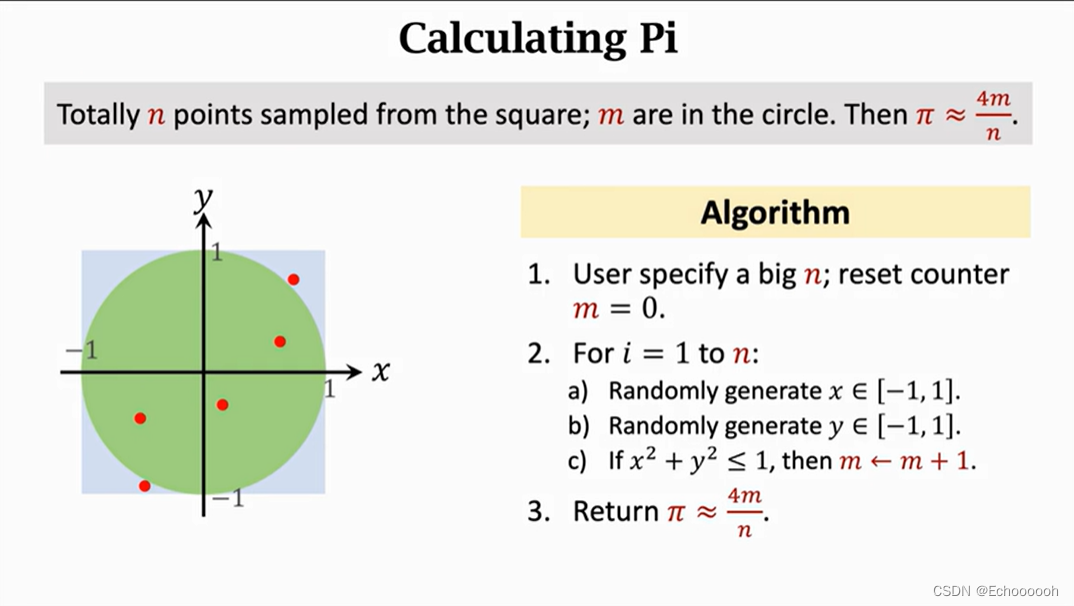
布封投针


估计阴影部分面积




近似求积分
一元函数求积分
2.中的式子也可以近似理解为,当样本足够多时可以近似认为时均匀分布,把积分理解为求函数曲线下的面积,整个图形的面积被切割为若干小细条的加和,小细条的底为平均每个细条的宽度,高为函数值。

多元函数求积分
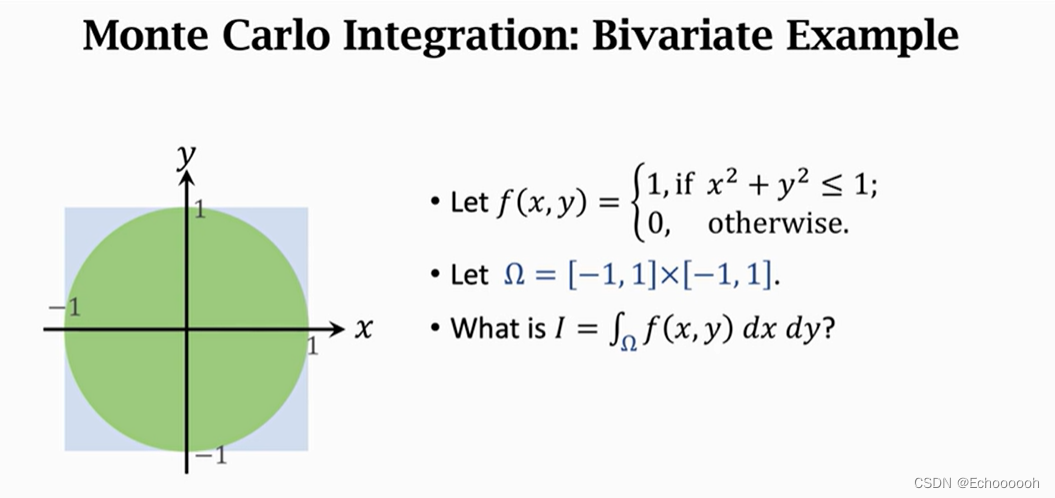

求期望(在统计和机器学习中非常有用)


抽样不再是均匀抽样,而是根据概率密度函数
p
(
x
)
p(x)
p(x)来抽样
补充知识:
蒙特卡洛的名字来源于摩纳哥的蒙特卡洛赌场
其他随机算法:
- 拉斯维加斯算法:结果总是正确 e.g. 随机快排
- 大西洋城算法:多项式时间复杂度,正确率大于75%
