位图详解.
1.位图概念
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中?
思考:
1.用哈希表?遍历一遍?时间复杂度O(N)
40亿个不重复无符号整数占多大内存?
10亿个字节大约是1个G
10亿个整数大约是4个G
40亿个整数大约是16个G
电脑的运行内存16个G,放不下
2.用快速排序+二分查找?时间复杂度 O(N*log2^N) + O(logN)
面临同样的问题,电脑的运行内存16个G,放不下
3.位图
数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,那么可以使用一个二进制比
特位来代表数据是否存在的信息,如果二进制比特位为1,代表存在,为0代表不存在。
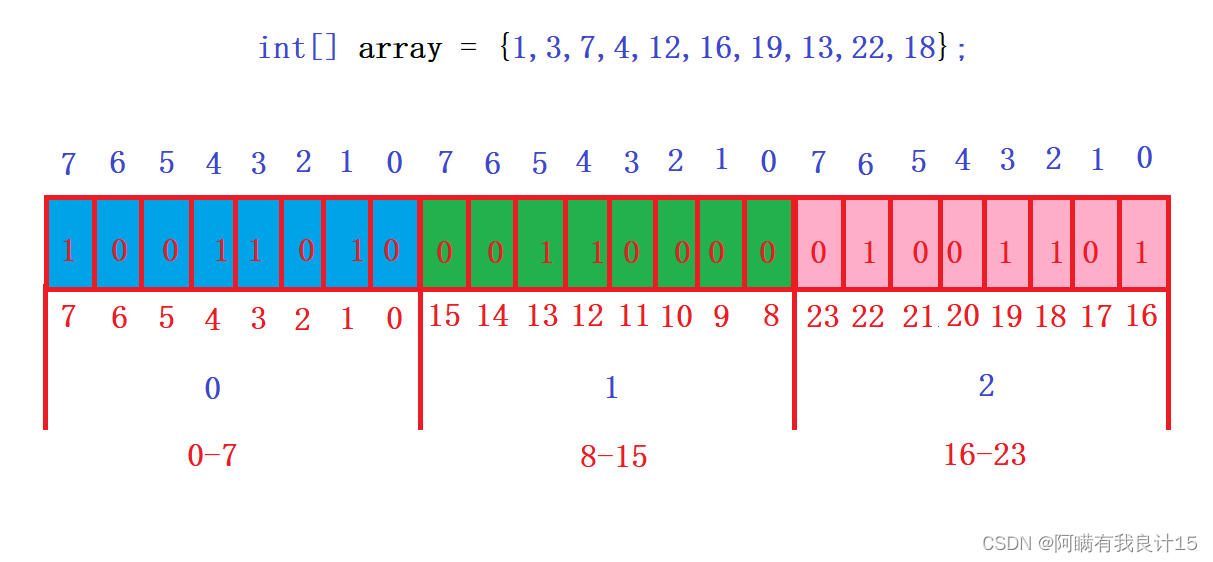
10个整数本应该存放40个字节,用到位图只需要3个字节
40亿个整数存放160亿个字节,用到位图只需要4 000 000 000 / 8 个字节
大约是4 000 000 000 / 8 / 1024 / 1024 = 476.837M(兆)
也就是说,我用476兆就能把40亿个数据表示出来,这就是位图的作用
2.适用场景
海量数据,整数,数据无重复的场景。通常是用来判断某个数据存不存在的。
3.举个例子
package test;
import java.util.BitSet;
public class Test {
public static void main(String[] args) {
int[] array = {1, 2, 3, 10, 4, 18, 13, 15};
BitSet bitSet = new BitSet();
for (int i = 0; i < array.length; i++) {
bitSet.set(array[i]);
}
System.out.println(bitSet.get(10));
System.out.println(bitSet.get(45));
}
}
4.具体实现
package test;
import java.util.Arrays;
public class MyBitSet {
public byte[] elem;
public int usedSize;
public MyBitSet() {
this.elem = new byte[1];
}
public MyBitSet(int n) {
this.elem = new byte[n / 8 + 1];
}
//设置某一位为一
public void set(int val) {
if (val < 0) {
System.out.println("只能为无符号整数,不能为负数");
throw new IndexOutOfBoundsException();
}
int arrayIndex = val / 8;
if (arrayIndex > elem.length - 1) {
elem = Arrays.copyOf(elem, arrayIndex + 1);
}
int bitIndex = val % 8;
elem[arrayIndex] |= (1 << bitIndex);
usedSize++;
}
public int getUsedSize() {
return usedSize;
}
//判断当前位 是不是1
public boolean get(int val) {
if (val < 0) {
System.out.println("只能为无符号整数,不能为负数");
throw new IndexOutOfBoundsException();
}
int arrayIndex = val / 8;
if (arrayIndex > elem.length - 1) {
elem = Arrays.copyOf(elem, arrayIndex + 1);
}
int bitIndex = val % 8;
if ((elem[arrayIndex] & (1 << bitIndex)) != 0) {
return true;
}
return false;
}
//将对应位置 置位0
public void reSet(int val) {
if (val < 0) {
System.out.println("只能为无符号整数,不能为负数");
throw new IndexOutOfBoundsException();
}
int arrayIndex = val / 8;
int bitIndex = val % 8;
elem[arrayIndex] &= ~(1 << bitIndex);
usedSize--;
}
public static void main(String[] args) {
MyBitSet myBitSet = new MyBitSet(22);
int[] array = {1, 3, 7, 4, 12, 16, 19, 13, 22, 18, 3};
for (int i = 0; i < array.length; i++) {
myBitSet.set(array[i]);
}
System.out.println(myBitSet.getUsedSize());
System.out.println(myBitSet.get(7788));
System.out.println(myBitSet.get(4));
//排序 时间复杂度O(N)
for (int i = 0; i < myBitSet.elem.length; i++) {
for (int j = 0; j < 8; j++) {
if ((myBitSet.elem[i] & (1 << j)) != 0) {
System.out.print((i * 8 + j) + " ");
}
}
}
}
}
