LeetCode 96. 不同的二叉搜索树

LeetCode 96. 不同的二叉搜索树

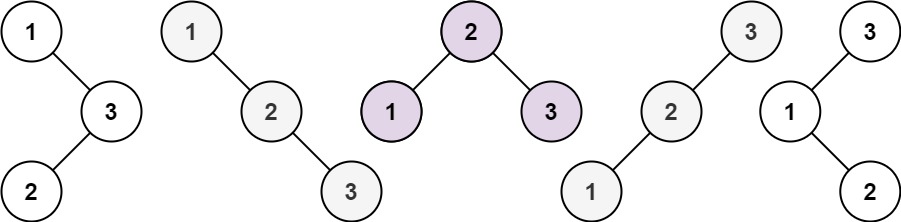
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

提示：

• 1 <= n <= 19

思路：

参考：LeetCode题解，包含图解。

1. 二叉搜索树：根的左孩子的值 < 根节点值，根的右孩子的值 > 根节点值
2. 只需取其中任意一个数i作为根，取这个数左边的数[0,i-1]构建左子树，取这个数右边的数[i+1,n]构建右子树即可
3. 此时左子树本身可能有m种构建方式，右子树有n种构建方式，所以取i作为根的二叉搜索树的种类为m*n
4. 对于整个序列1~n都可能作为根节点，根有n种可能。所以整个序列构建二叉搜索树，所有种类等于分别取1~n为根的二叉搜索树种类和
5. 注意 特殊边界：dp[0]为0个数构成的二叉搜索树种类为1，因为null可以认为是一颗 空二叉搜索树

举例：

在排除根节点本身所占的一个节点数后，前面一项是左子树情况数，后面一项是右子树情况数，相加即可。比如这里求解n=3的情况：

节点数组为[1,2,3]，dp[3] = dp[0]*dp[2] + dp[1]*dp[1] + dp[2]*dp[0]，可以理解成：

• 根节点为 1 时：因为没有比1小的节点，所以左子树可能的情况数为0；又因为 2,3 > 1，所以右子树可能情况数为2，dp[0]*dp[2] = 1*2=2
• 根节点为 2 时：因为 1 < 2 ，所以左子树可能的情况数为1；又因为 3 > 2，所以右子树可能情况数也为1，dp[1]*dp[1] = 1*1=1
• 根节点为 3 时：因为1,2 < 3，所以左子树可能的情况数为2；又因为没有比3大的节点，右子树可能情况数为0，dp[2]*dp[0] = 2*1=2
• 所以一共的可能数：2 + 1 + 2= 5，其中dp[2]可以分别表示为以 1或2 为根节点的二叉搜索树，所以 dp[2] = 2，dp[0] = 1 表示为空二叉搜索树，dp[1] = 1表示仅有一个节点的二叉搜索树。

时间复杂度：

空间复杂度：

/* 
    思路：参考：https://leetcode.cn/problems/unique-binary-search-trees/solutions/6693/hua-jie-suan-fa-96-bu-tong-de-er-cha-sou-suo-shu-b/
    
    1. 二叉搜索树：根的左孩子的值 < 根节点值，根的右孩子的值 > 根节点值
    2. 只需取其中任意一个数i作为根，取这个数左边的数[0,i-1]构建左子树，取这个数右边的数[i+1,n]构建右子树即可
    3. 此时左子树本身可能有m种构建方式，右子树有n种构建方式，所以取i作为根的二叉搜索树的种类为m*n
    4. 对于整个序列1~n都可能作为根节点，根有n种可能。所以整个序列构建二叉搜索树，所有种类等于分别取1~n为根的二叉搜索树种类和
*/

func numTrees(n int) int {
    dp := make([]int, n+1)
    // 特殊边界：dp[0]为0个数构成的二叉搜索树种类为1，因为null可以认为是一颗空二叉搜索树
    dp[0], dp[1] = 1, 1 

    // 当节点数量为i时，从前往后依次递推
    for i := 2; i <= n; i++ {       
        // 因为根节点本身也要占1个节点数量，排除根节点本身后，所以 j <= i-1 → j < i
        for j := 0; j < i; j++ {
            // 前一项dp[j]是左子树的种数，后一项dp[i-j-1]是右子树种数，相加即可
            // 举例：dp[3] = dp[0]*dp[2] + dp[1]*dp[1] + dp[2]*dp[0]
            // 可以理解成：在排除根节点本身所占的一个节点数后，前面一项是左子树情况数，后面一项是右子树情况数，相加即可
            dp[i] += (dp[j]*dp[i-j-1])
        }
    }

    return dp[n]
}