当前位置： 首页 > news >正文

电磁功率流和坡印廷矢量

news 来源：原创 2024/11/18 1:36:09

回顾：

场源的影响周围的快慢取决于距离和传播速度

场源变化引起电磁波，电磁波传输能量

w=w_e+w_m=\frac{1}{2} \vec D \cdot \vec E+\frac{1}{2}\vec B \cdot \vec H

电磁能量的流动满足能量守恒定律

我们关心的是

体积V里面和体积外怎么交换能量，S是包围的闭合面

大家想一想，体积里面有场源

随着能量的增长，不断向外辐射能量

现在关心的是体积内部和外部怎么进行能量交换

体积里面的总电磁能量W=\int_V \frac{1}{2} \vec D \cdot \vec E+\frac{1}{2}\vec B \cdot \vec HdV

这个体积里面的能量随着时间的变化率

变化率就是关于世间的偏导数，假定体积不随时间变化

由此公式转化为

\frac{\partial w}{\partial t} =\int_V [\frac{\partial}{\partial t}(\frac{1}{2}\vec D \cdot \vec E)+\frac{\partial }{\partial t}(\frac{1}{2}\vec B \cdot \vec H )]dV

\frac{\partial}{\partial t}(\frac{1}{2}\vec D \cdot \vec E)=\frac{\partial }{\partial t}(\frac{1}{2}\varepsilon \vec E^2)=\varepsilon \vec E \frac{\partial E}{\partial t}

现在我们再改变一下，假定介质的介电常数不随时间变化（非色散介质）

意味着介电常数不随时间变化

\varepsilon \vec E \frac{\partial E}{\partial t}=\vec E \cdot \frac{\partial \vec D}{\partial t}

同理我们可以得到

\frac{\partial }{\partial t}(\frac{1}{2}\vec B \cdot \vec H )=\vec H \cdot \frac{\partial \vec B}{\partial t}

现在我们把关系再处理处理

大家看，我们这个又可以写成

=\vec E \cdot(\nabla \times \vec H -\vec J),=\vec H \cdot (-\nabla \times \vec E)

由此我们可以得到

\frac{\partial w}{\partial t}=\int_V [\vec E \cdot \nabla \times \vec H -\vec E \cdot \vec J -\vec H \cdot \nabla \times \vec E]dV

现在我们同时乘以负号，再进行合并

-\frac{\partial w}{\partial t}=\int_V \nabla \cdot(\vec E \times \vec H )dV+\int_V \vec E \times \vec J dV

现在再来看一下物理含义

如果现在体积V里面没有场源，此时我们现在里面是导电媒质

一旦电磁波进入，电磁波里面有电场分量，电场就要驱动形成传导电流

传导电流不止是在有源的地方存在，在有电场有导电能力的地方就会存在

如果没有负号，左边代表电磁能量的增长率

右边第二项是导电媒质引起的焦耳损耗的能量，只能靠电磁能量来减少

还有右边第一项

我们把关系式再写一下

-\frac{\partial w}{\partial t}=\int_V \frac{J^2}{\Gamma}dV +\oint_S (\vec E \times \vec H )\cdot d \vec A

现在这个方程右边第一项是导电媒质的损耗，还有一部分就是穿出去的通量

实际上就是我们的体积V供应给外部的能量

反映了这样的事实，一部分供应给内部，一部分供应给外部

反映了体积V内外交换电磁场的能量

不是发生在一个点，而是在所有点上都会发生

最大的方向出现在\vec E \times \vec H上

我们称之为坡印廷矢量

如果S和坡印廷矢量一致的话，表示单位时间穿过与S垂直的单位面积能量的多少

我们把这个定律称为能量的守恒与转化定律，也就是坡印廷定律

-\frac{\partial w}{\partial t}=\int_V \frac{J^2}{\Gamma}dV +\oint_S (\vec E \times \vec H )\cdot d \vec A

我们看到能量流动的方向与电场，磁场相互垂直，在他们所构成的平面的法线方向

如果现在我们分析的是恒定场，电场磁场不随着时间变化

电磁能量不随着时间变化，在守恒变化里面，对时间的偏导数等于0

体积里面的焦耳损耗还是发生的

\int_V \frac{J^2}{\Gamma}dV =- \oint_S (\vec E \times \vec H )\cdot d \vec A

损耗的能量只能靠外部的电磁场源源不断地提供，我们得到了电磁能量的传递者仍然是电磁场

能量的载体不是电荷或者电流而是电磁场

 

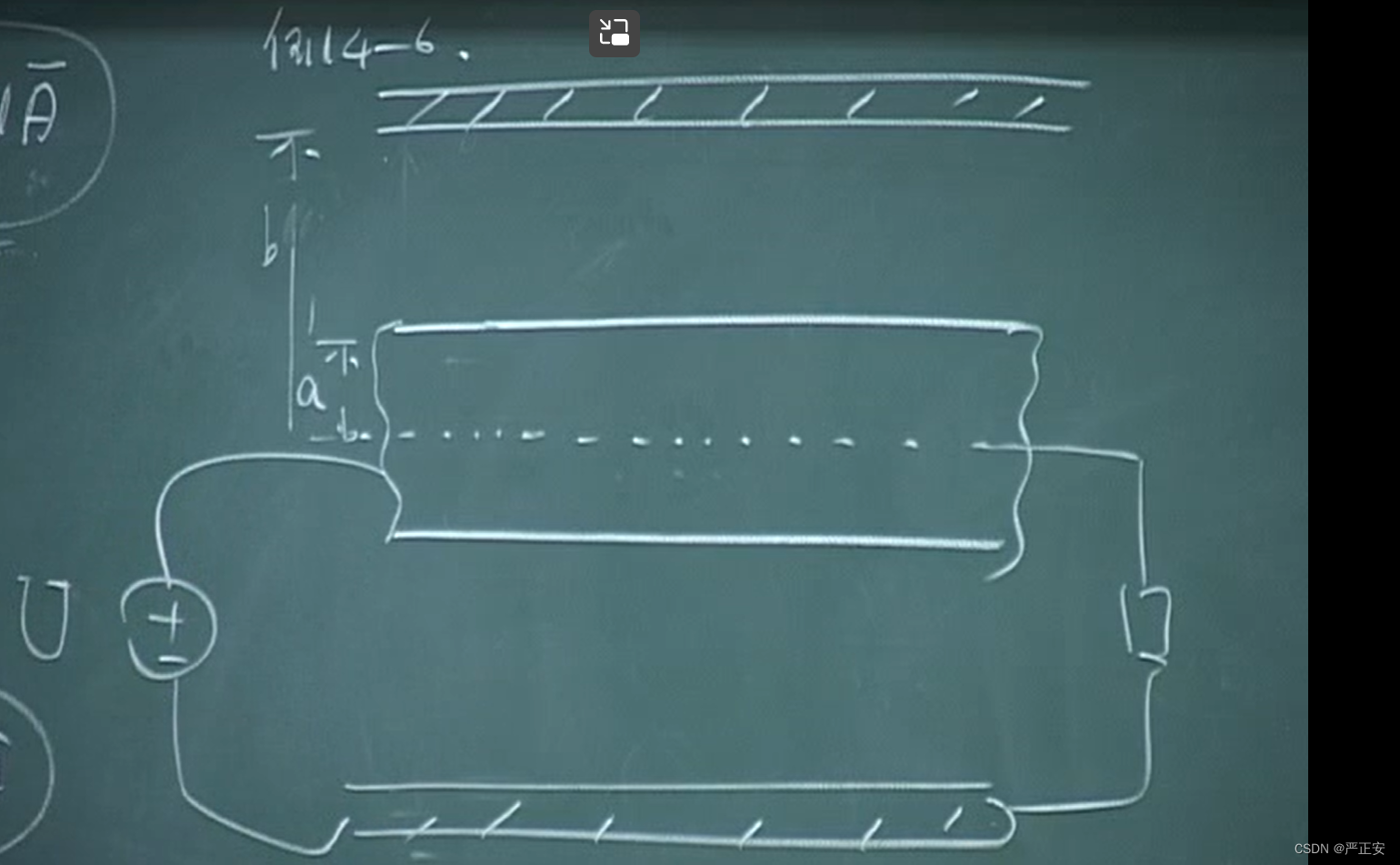
 电缆就是把电源的能量定向传递给负载

我们现在就想知道电源把能量传递给负载，是在外部流动呢还是在电磁场里面流动呢

如果导体介质都是理想的

那么在里面电场磁场强度都为0

在内导体的内部，坡印廷矢量等于0

我们看到在导体内部没有能量流动

 我们看电场强度的方向 和磁场强度的方向

 坡印廷方向沿着轴线方向

\vec S =\vec E \times \vec H =\frac{UI}{2 \pi \rho^2 ln(\frac{b}{a})}\vec e_z

能量流动在介质中不在导体里面

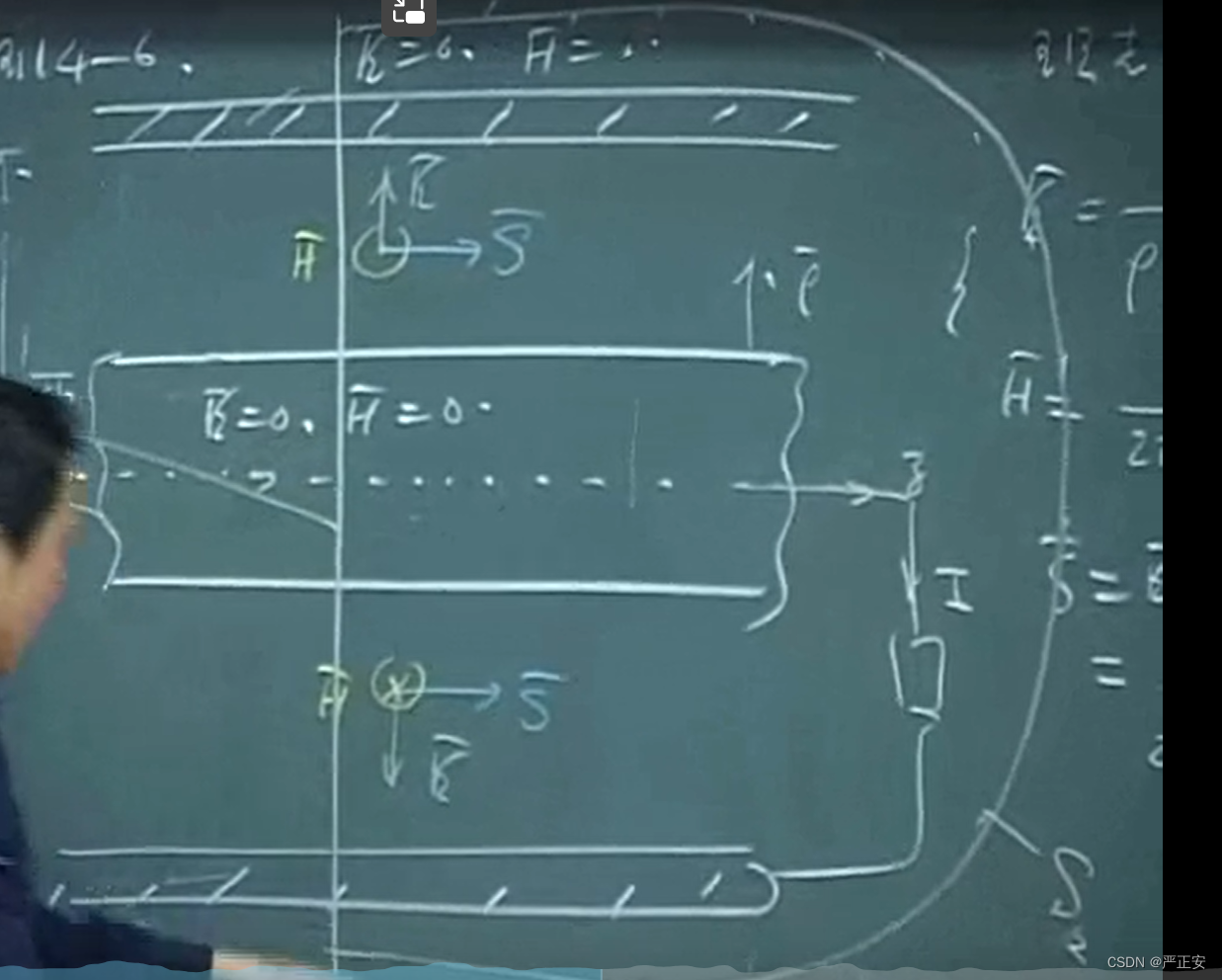
 然后我们取一个闭合面

我们就可以得到

\int \frac{UI}{2 \pi \rho ln \frac{b}{a}}2 \pi \rho d \rho

这个的积分就是流进体积内部的功率，作为损耗，我们说这个功率我们记为P

P=UI

我们电源提供的功率通过介质从电源流向负载

因此电磁场是能量的载体

那既然导体不是能量的载体，那我们要导体干什么

导体是支撑电磁场的结构，起到导引和支撑电磁场的作用

下面就是不是理想电磁场

 

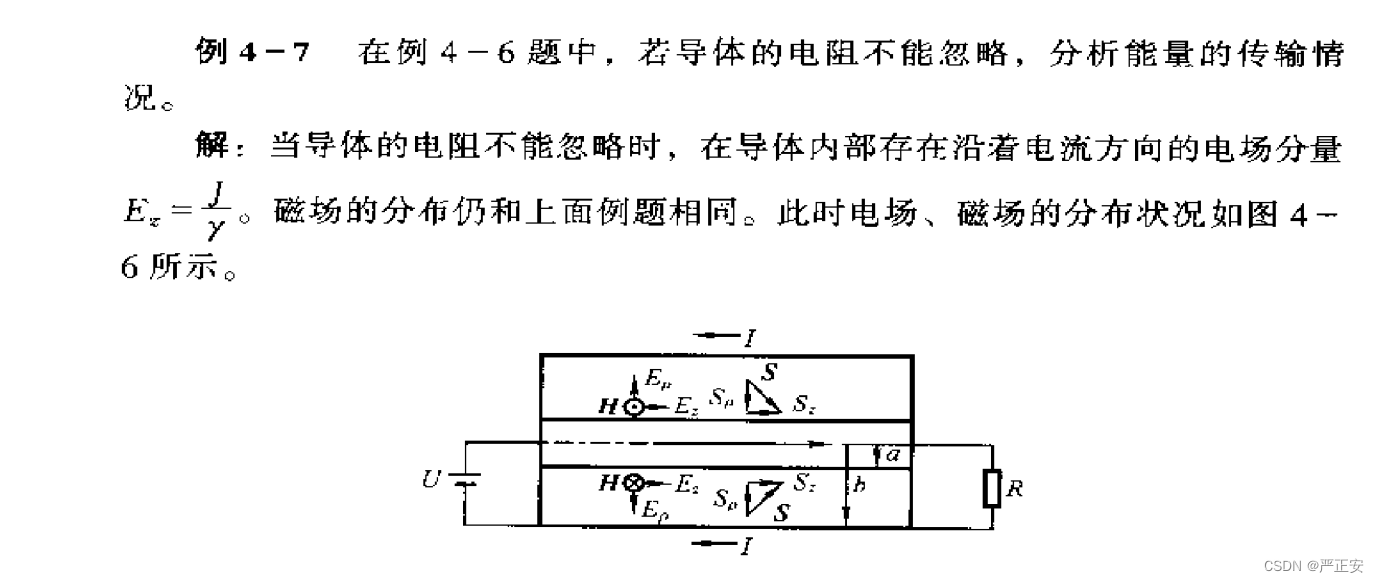
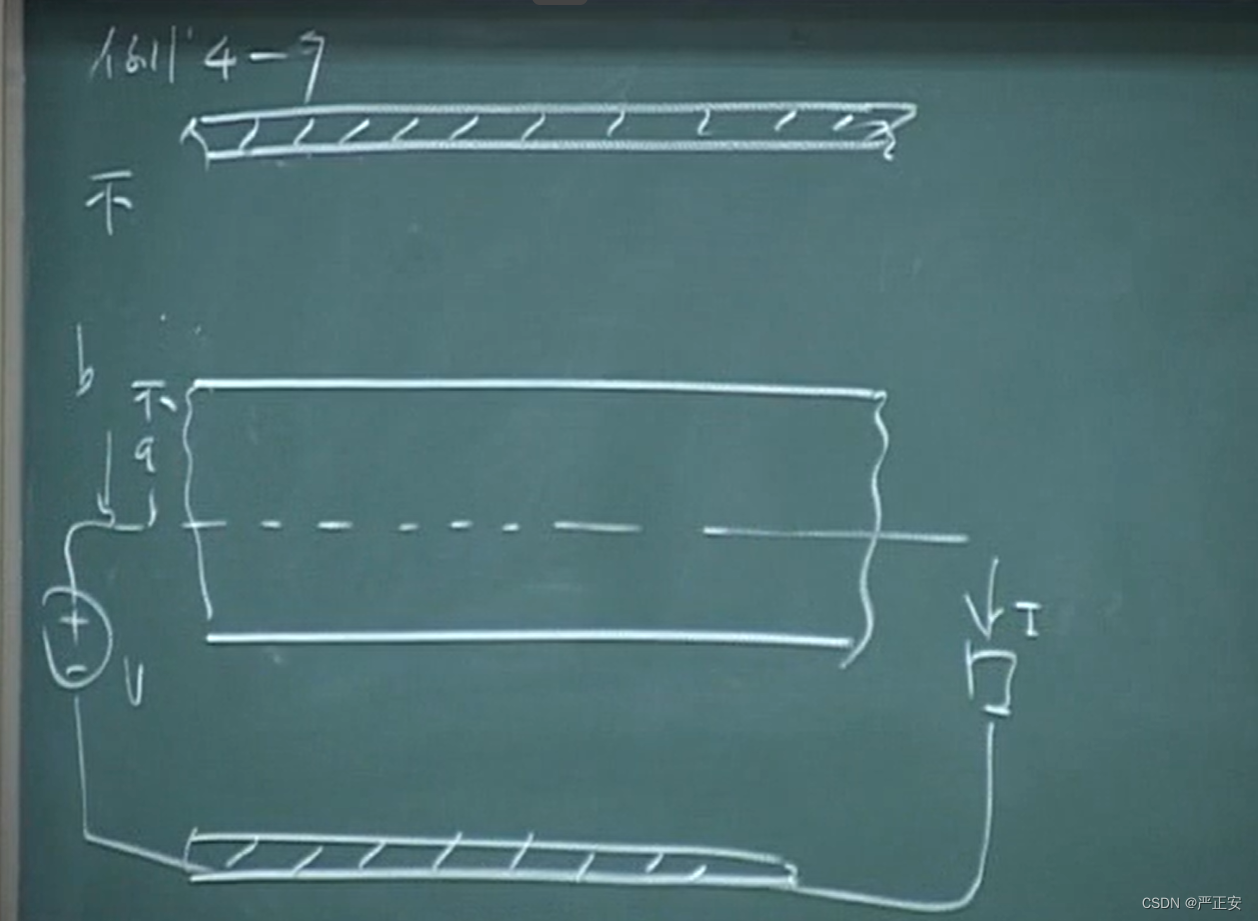
 导体内部流过电流，那就有电场强度

电流只有轴线方向的分量

直流电是均匀分布的

\vec E =\frac{I}{\pi a^2 \Gamma}\vec e_z

\rho <a, \vec H =\frac{I^{\prime}}{2 \pi \rho }\vec e_\varphi

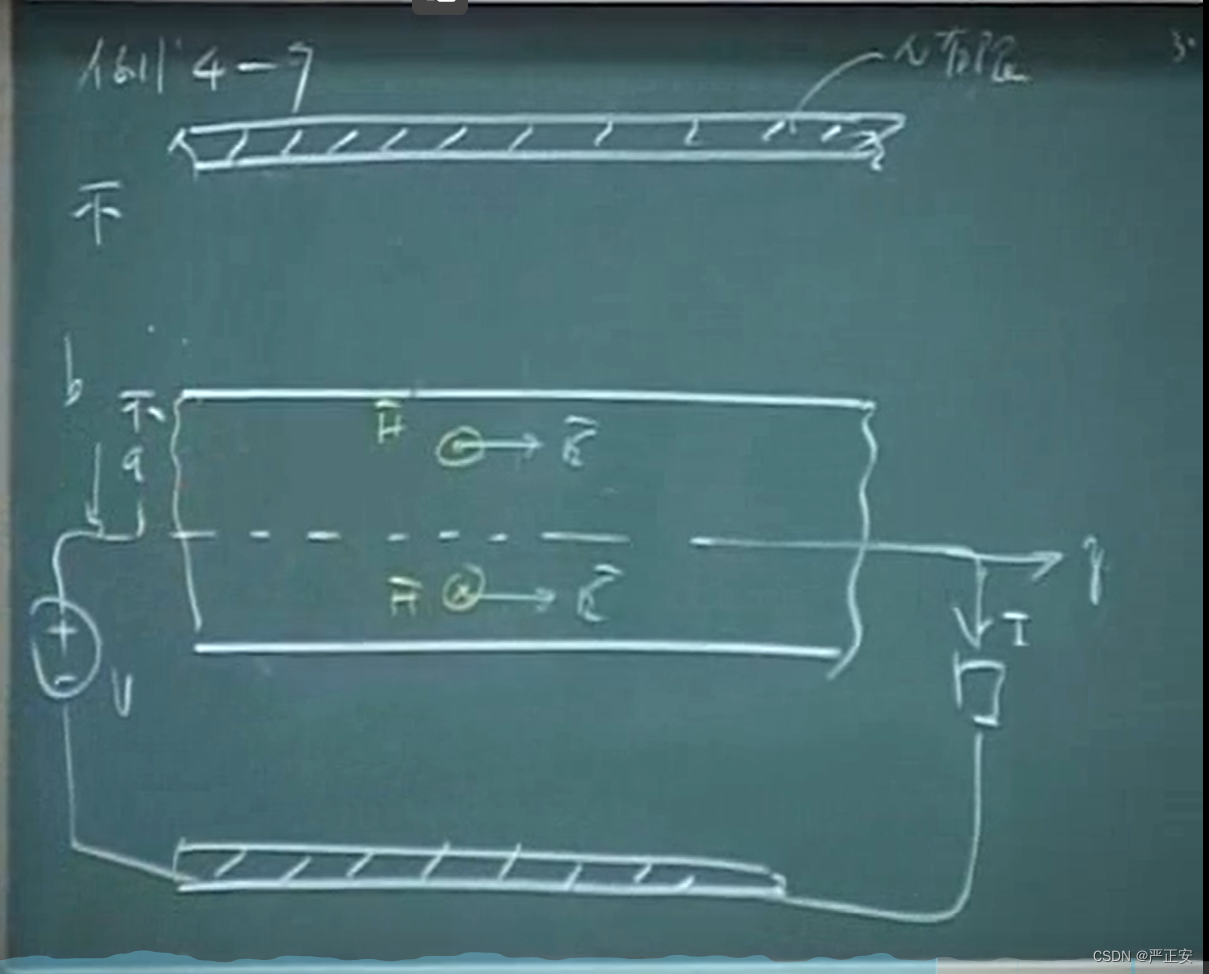
 坡印廷向量水平向右

 

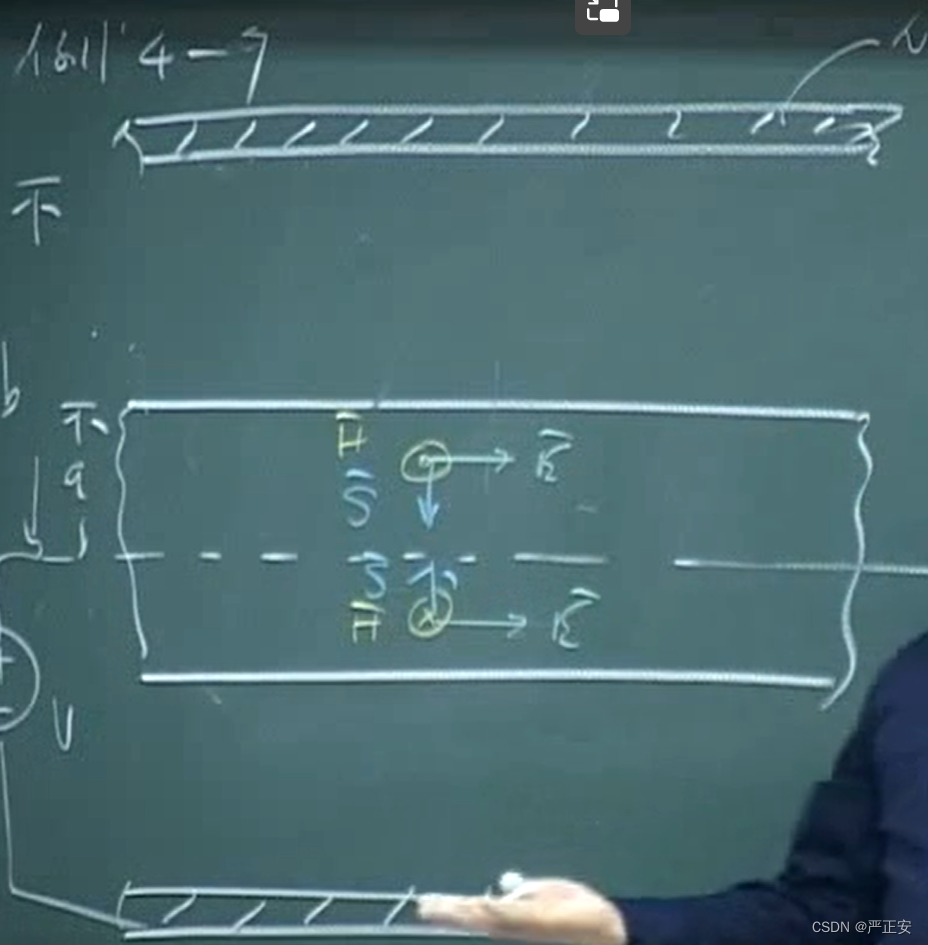
a<\rho<b,\vec H =\frac{I}{2 \pi \rho}\vec e_{\varphi},\vec E=E_\rho \vec e_{\rho}

我们再看电场强度一定有Z方向的分量

我们的电场

\vec S =\vec E \times \vec H =S_z\vec e_z +S_\rho \vec e_\rho 

 

        

相关文章：

  • 网站主页样式/seo免费自学的网站
  • wordpress播放pdf/开发网站建设
  • 不需要证件做网站/精准客源推广引流
  • wordpress远程ftp/seo培训公司
  • 今天发布手机/seo外包公司一般费用是多少
  • 如何制造公司网站/关键词点击排名系统
  • 远离不恰当的运动方式，缤跃酒店满足大众对专业化、品质化健身场所的需求！
  • 变频变风量通风系统如何选择
  • python---数据库操作
  • 面试题题review
  • Android studio配置大内存，编译速度更快！
  • 20-Mysql内核查询优化规则详解
  • 训练yolo系列+deepsort模式的跟踪器（一）：训练deepsort
  • Shape详解
  • 修改主机名和ip地址之后需重新reconfigure GI
  • 开源项目-OA自动化管理系统
  • spring-boot如何自行写一个starter并且使用
  • 轻松入门基因表达式编程 （GEP）