实验三 多层神经网络
一、实验目的
(1)学习并掌握常见的机器学习方法;
(2)能够结合所学的python知识实现机器学习算法;
(3)能够用所学的机器学习算法解决实际问题。
二、实验内容与要求
(1)理解多层神经网络的架构及参数更新,能够结合多层神经网络实现分类问题;
(2)根据所提供的代码,完成多层神经网络的代码,能够进行分类与回归;
(3)能够正确输出结果
三、实验过程及代码
3.1 初始化参数
(1)初始化两层网络参数
| def initialize_parameters(n_x,n_h,n_y): W1 = np.random.randn(n_h, n_x) * 0.01 b1 = np.zeros((n_h, 1)) W2 = np.random.randn(n_y, n_h) * 0.01 b2 = np.zeros((n_y, 1))
#使用断言确保我的数据格式是正确的 assert(W1.shape == (n_h, n_x)) assert(b1.shape == (n_h, 1)) assert(W2.shape == (n_y, n_h)) assert(b2.shape == (n_y, 1))
parameters = {"W1": W1, "b1": b1, "W2": W2, "b2": b2}
return parameters |
(2)初始化多层网络参数
| def initialize_parameters_deep(layers_dims): np.random.seed(3) parameters = {} L = len(layers_dims)
for l in range(1,L): parameters["W" + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) / np.sqrt(layers_dims[l - 1]) parameters["b" + str(l)] = np.zeros((layers_dims[l], 1))
#确保我要的数据的格式是正确的 assert(parameters["W" + str(l)].shape == (layers_dims[l], layers_dims[l-1])) assert(parameters["b" + str(l)].shape == (layers_dims[l], 1))
return parameters |
3.2 前向传播分
分两步,同时保存A_pre,w,b,Z,A
(1)线性前向传播
| def linear_forward(A_prev,W,b): """ 实现前向传播的线性部分。 参数: A_prev - 来自上一层(或输入数据)的激活,维度为(上一层的节点数量,示例的数量) W - 权重矩阵,numpy数组,维度为(当前图层的节点数量,前一图层的节点数量) b - 偏向量,numpy向量,维度为(当前图层节点数量,1) 返回: Z - 激活功能的输入,也称为预激活参数 cache - 一个包含“A”,“W”和“b”的字典,存储这些变量以有效地计算后向传递 """ #Please do something return Z,linear_cache |
(2)激活函数前向传播
| def linear_activation_forward(A_prev,W,b,activation): """ 实现LINEAR-> ACTIVATION 这一层的前向传播 参数: A_prev - 来自上一层(或输入层)的激活,维度为(上一层的节点数量,示例数) W - 权重矩阵,numpy数组,维度为(当前层的节点数量,前一层的大小) b - 偏向量,numpy阵列,维度为(当前层的节点数量,1) activation - 选择在此层中使用的激活函数名,字符串类型,【"sigmoid" | "relu"】 返回: A - 激活函数的输出,也称为激活后的值 cache - 一个包含“linear_cache”和“activation_cache”的字典,我们需要存储它以有效地计算后向传递 """ #Please do something return A,cache |
3.3 model的前向传播
| def L_model_forward(X,parameters): """ 实现[LINEAR-> RELU] *(L-1) - > LINEAR-> SIGMOID计算前向传播,也就是多层网络的前向传播,为后面每一层都执行LINEAR和ACTIVATION
参数: X - 数据,numpy数组,维度为(输入节点数量,示例数) parameters - initialize_parameters_deep()的输出
返回: AL - 最后的激活值 caches - 包含以下内容的缓存列表: linear_relu_forward()的每个cache(有L-1个,索引为从0到L-2) linear_sigmoid_forward()的cache(只有一个,索引为L-1) """ #Please do something
return AL,caches |
3.4 计算cost function
| def compute_cost(AL,Y): """ 交叉熵误差函数,定义成本函数。 参数: AL - 与标签预测相对应的概率向量,维度为(1,示例数量) Y - 标签向量(例如:如果不是猫,则为0,如果是猫则为1),维度为(1,数量) 返回: cost - 交叉熵成本 """ #Please do something return cost |
3.5 反向传播
(1)反向传播用于计算相对于参数的损失函数的梯度,向前和向后传播的流程图如下:
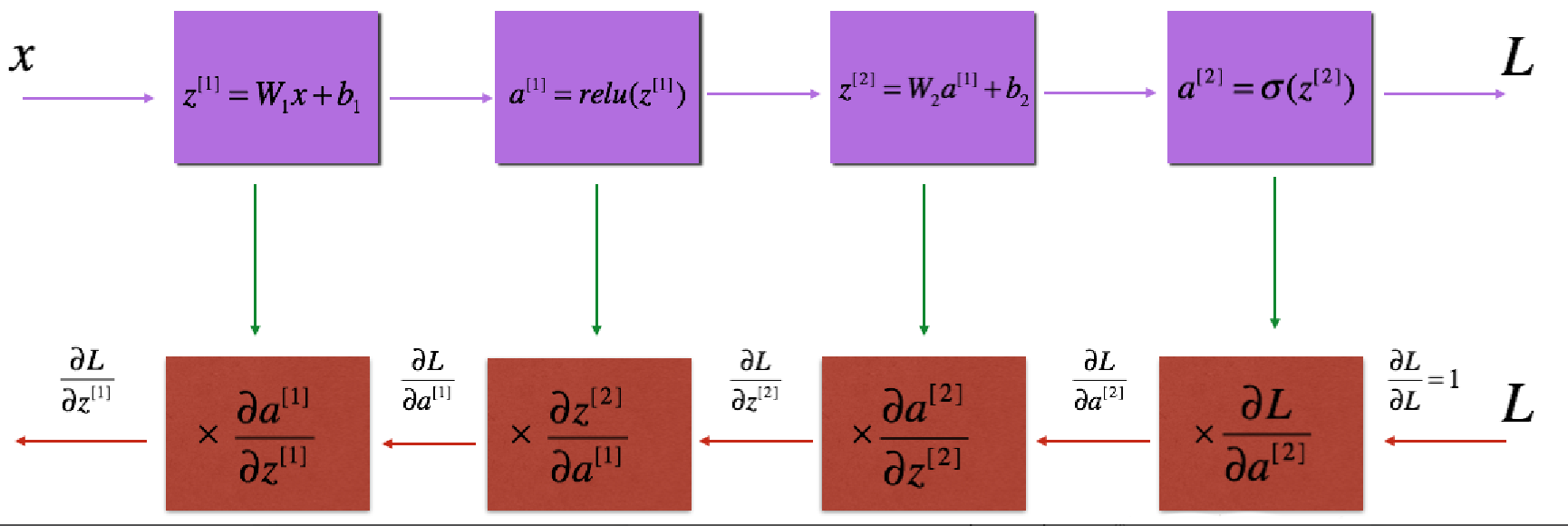
(2)对于线性的部分的公式:
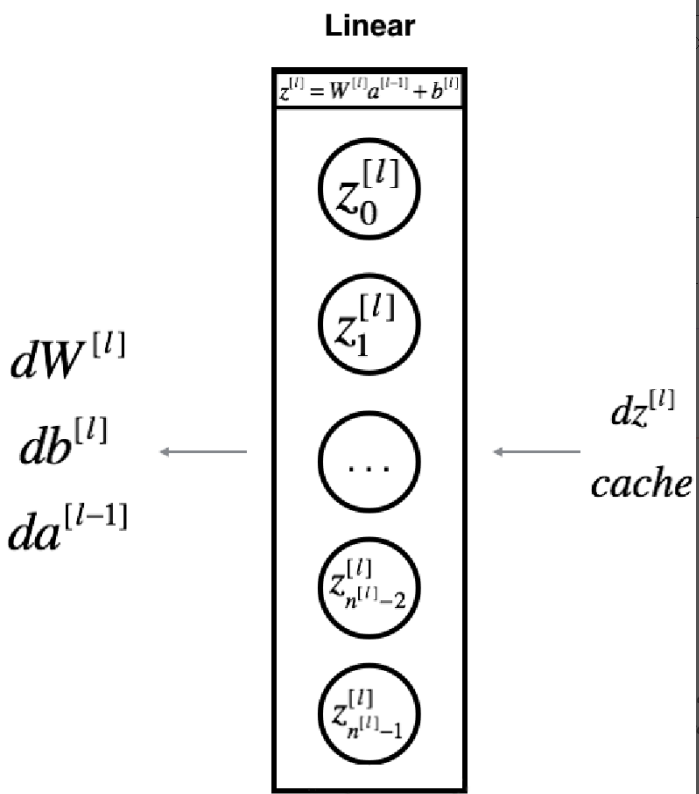
(3)单层实现反向传播的线性部分
| def linear_backward(dZ,linear_cache): """ 为单层实现反向传播的线性部分(第L层) 参数: dZ - 相对于(当前第l层的)线性输出的成本梯度 cache - 来自当前层前向传播的值的元组(A_prev,W,b) 返回: dA_prev - 相对于激活(前一层l-1)的成本梯度,与A_prev维度相同 dW - 相对于W(当前层l)的成本梯度,与W的维度相同 db - 相对于b(当前层l)的成本梯度,与b维度相同 """ #Please do something
return dA_prev, dW, db |
(4)实现LINEAR-> ACTIVATION层的后向传播
| def linear_activation_backward(dA,cache,activation="relu"): |
(5)多层网络的向后传播
| def L_model_backward(AL,Y,caches): """ 对[LINEAR-> RELU] *(L-1) - > LINEAR - > SIGMOID组执行反向传播,就是多层网络的向后传播 参数: AL - 概率向量,正向传播的输出(L_model_forward()) Y - 标签向量(例如:如果不是猫,则为0,如果是猫则为1),维度为(1,数量) caches - 包含以下内容的cache列表: linear_activation_forward("relu")的cache,不包含输出层 linear_activation_forward("sigmoid")的cache
返回: grads - 具有梯度值的字典 grads [“dA”+ str(l)] = ... grads [“dW”+ str(l)] = ... grads [“db”+ str(l)] = ... """ #Please do something return grads |
3.6 更新参数
| def update_parameters(parameters, grads, learning_rate): |
四、实验分析及总结
(1)两层神经网络测试结果:


(2)多层神经网络测试结果:


(3)真实样本测试:
测试图片: 测试结果:
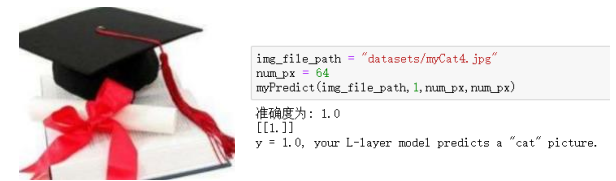
测试图片: 测试结果:
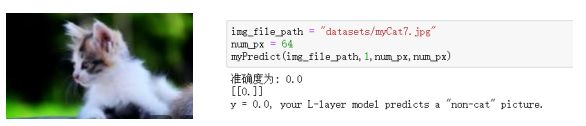
单来说就是将单个感知器作为一个神经网络节点,然后用此类节点组成一个层次网络结构,我们称此网络即为人工神经网络(本人自己的理解)。当网络的层次大于等于3层(输入层+隐藏层(大于等于1)+输出层)时,我们称之为多层神经网络。
对于反向传播算法主要从以下几个方面进行总结:
(1)局部极小值:对于多层网络,误差曲面可能含有多个不同的局部极小值,梯度下降可能导致陷入局部极小值。缓解局部极小值的方法主要有增加冲量项,使用随机梯度下降,多次使用不同的初始权值训练网络等。
(2)权值过多:当隐藏节点越多,层数越多时,权值成倍的增长。权值的增长意味着对应的空间的维数越高,过高的维数易导致训练后期的过拟合。
(3)过拟合:当网络的训练次数过多时,可能会出现过拟合的情况。解决过拟合主要两种方法:一种是使用权值衰减的方式,即每次迭代过程中以某个较小的因子降低每个权值;另一种方法就是使用验证集的方式来找出使得验证集误差最小的权值,对训练集较小时可以使用交叉验证等。
(4)算法终止策略:当迭代次数达到设定的阀值时,或者损失函数小于设定的阀值时。
结果显示:训练集高,测试集低,稍微有点过拟合。
处理过拟合的方法:1.减少特征个数 2.增加lamda的值。
