概要

前文介绍了贝叶斯公式基础以及在统计领域的基本应用贝叶斯基础_zhanglehes的博客-CSDN博客，本文将介绍它的一种新的转换形式，以及在机器分类领域的应用。

分类的数学描述

朴素贝叶斯公式推理

贝叶斯公式

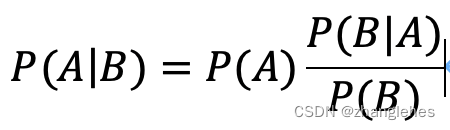
在分类领域，将其改写如下

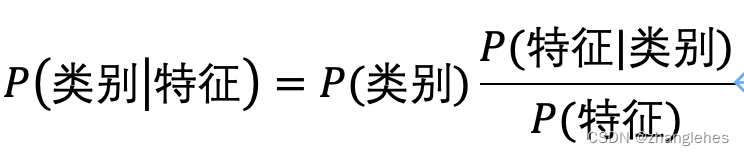
我们知道，特征通常是一个向量值

再次改写公式如下

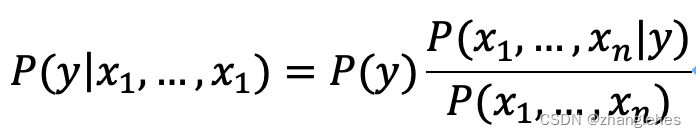
在这儿，公式中的“朴素”二字开始发挥作用了。它有如下两个假设：

1. 所有的特征是相互独立的，也就是x1的取值不影响到x2的取值；
2. 所有特征的重要性是一样的

再次改写公式

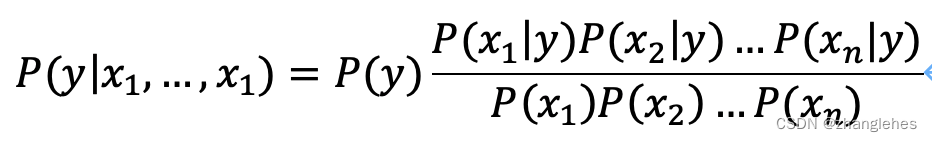
在分类领域，等式右边的分母为一常量，当必要不同分类概率大小时，该常量客户来，这样能减少计算量

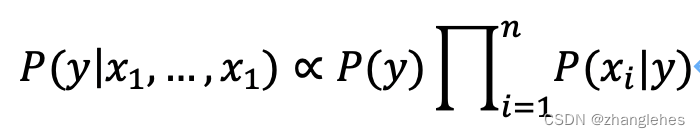
上面两个公式就是朴素贝叶斯公式。通过大数据统计的方式，可以分别求出等式右边各个参数的值，进而可以比较不同分类的概率大小。

朴素贝叶斯发散

1、上面介绍的是基于离散特征值的处理方式，其实如果特征值是连续的，也是可以按照上述流程处理的，如分类在某一特征值的变化满足高斯分布；

2、上面公式在计算等式右边的概率时，还可以添加时间出现的频率作为影响因子；

小结

朴素贝叶斯的公式比较简单，计算量不大，这是它的优势。

同时基于“朴素”的两个假设，在一些场景下是不合适的，导致其分类的效果不佳。

参考文献

1. 带你理解朴素贝叶斯分类算法 - 知乎
2. https://www.geeksforgeeks.org/naive-bayes-classifiers/