当前位置： 首页 > news >正文

Transformer模型详解相关了解

news 来源：原创 2024/11/19 5:36:18

文章目录

  • Transformer模型详解
    • 1.前言
      • 1.1 Transformer 整体结构
      • 1.2 Transformer 的工作流程
    • 2. Transformer 的输入
      • 2.1 单词 Embedding
      • 2.2 位置 Embedding
    • 3. Self-Attention（自注意力机制）
      • 3.1 Self-Attention 结构
      • 3.2 Q, K, V 的计算
      • 3.3 Self-Attention 的输出
      • 3.4 Multi-Head Attention
    • 4. Encoder 结构
      • 4.1 Add & Norm
      • 4.2 Feed Forward
      • 4.3 组成 Encoder
    • 5. Decoder 结构
      • 5.1 第一个 Multi-Head Attentionwd
      • 5.2 第二个 Multi-Head Attention
      • 5.3 Softmax 预测输出单词
    • 6.Transformer 总结
    • 参考

Transformer模型详解

1.前言

Transformer由论文《Attention is All You Need》提出，现在是谷歌云TPU推荐的参考模型。论文相关的Tensorflow的代码可以从GitHub获取，其作为Tensor2Tensor包的一部分。

1.1 Transformer 整体结构

Transformer 用于中英文翻译的整体结构

img
 Transformer 的整体结构，左图Encoder和右图Decoder  \text { Transformer 的整体结构，左图Encoder和右图Decoder }  Transformer 的整体结构，左图Encoder和右图Decoder 
Transformer 由 Encoder 和 Decoder 两个部分组成，Encoder 和 Decoder 都包含 6 个 block。

1.2 Transformer 的工作流程

  1. **获取输入句子的每一个单词的表示向量 X，X由单词的 Embedding（Embedding就是从原始数据提取出来的Feature） 和单词位置的 Embedding 相加得到。

img
 Transformer 的输入表示  \text { Transformer 的输入表示 }  Transformer 的输入表示 

  1. 将得到的单词表示向量矩阵 (如下图所示，每一行是一个单词的表示 x) 传入 Encoder 中，经过 6 个 Encoder block 后可以得到句子所有单词的编码信息矩阵 C \mathbf{C} C ，如下图。单词向量矩 阵用 X n × d X_{n \times d} Xn×d​ 表示， n \mathrm{n} n 是句子中单词个数， d \mathrm{d} d 是表示向量的维度 (论文中 d = 512 \mathrm{d}=512 d=512 )。每一个 Encoder block 输出的矩阵维度与输入完全一致。

img
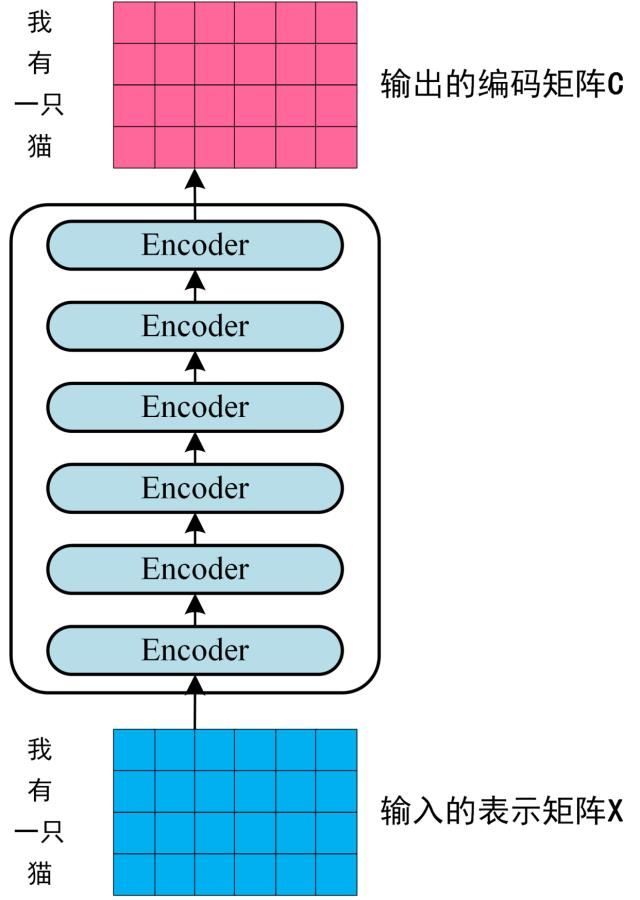
 Transformer Encoder 编码句子信息  \text { Transformer Encoder 编码句子信息 }  Transformer Encoder 编码句子信息 

  1. 将 Encoder 输出的编码信息矩阵 C传递到 Decoder 中，Decoder 依次会根据当前翻译过的单词 1~ i 翻译下一个单词 i+1，如下图所示。在使用的过程中，翻译到单词 i+1 的时候需要通过 Mask (掩盖) 操作遮盖住 i+1 之后的单词。

img
T r a n s o f r m e r D e c o d e r 预测 Transofrmer Decoder 预测 TransofrmerDecoder预测
上图 Decoder 接收了 Encoder 的编码矩阵 C，然后首先输入一个翻译开始符 “”，预测第一个单词 “I”；然后输入翻译开始符 “” 和单词 “I”，预测单词 “have”，以此类推。这是 Transformer 使用时候的大致流程，接下来是里面各个部分的细节。

2. Transformer 的输入

Transformer 中单词的输入表示 x由单词 Embedding 和位置 Embedding （Positional Encoding）相加得到。

img

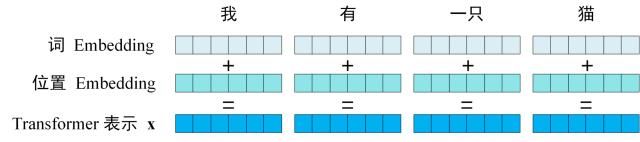
2.1 单词 Embedding

# 单词Embedding，可以利用nn.Embedding
#  i_vocab_size：输入词向量维度大小 hidden_size ：隐藏层大小
i_vocab_embedding = nn.Embedding(i_vocab_size,hidden_size)

单词的 Embedding 有很多种方式可以获取，例如可以采用 Word2Vec、Glove 等算法预训练得到，也可以在 Transformer 中训练得到。

class Embeddings(nn.Module):
    def __init__(self, d_model, vocab):
        """
        类的初始化函数
        d_model：指词嵌入的维度
        vocab:指词表的大小
        """
        super(Embeddings, self).__init__()
        #之后就是调用nn中的预定义层Embedding，获得一个词嵌入对象self.lut
        self.lut = nn.Embedding(vocab, d_model)
        #最后就是将d_model传入类中
        self.d_model =d_model
    def forward(self, x):
        """
        Embedding层的前向传播逻辑
        参数x：这里代表输入给模型的单词文本通过词表映射后的one-hot向量
        将x传给self.lut并与根号下self.d_model相乘作为结果返回
        """
        embedds = self.lut(x)
        return embedds * math.sqrt(self.d_model)

2.2 位置 Embedding

Transformer 中除了单词的 Embedding，还需要使用位置 Embedding 表示单词出现在句子中的位置。**因为 Transformer 不采用 RNN 的结构，而是使用全局信息，不能利用单词的顺序信息，而这部分信息对于 NLP 来说非常重要。**所以 Transformer 中使用位置 Embedding 保存单词在序列中的相对或绝对位置。

位置 Embedding 用 PE表示，PE 的维度与单词 Embedding 是一样的。PE 可以通过训练得到， 也可以使用某种公式计算得到。在 Transformer 中采用了后者，计算公式如下:
P E ( p o s , 2 i ) = sin ⁡ ( p o s / 1000 0 2 i / d ) P E ( p o s , 2 i + 1 ) = cos ⁡ ( p o s / 1000 0 2 i / d ) \begin{gathered} P E_{(p o s, 2 i)}=\sin \left(p o s / 10000^{2 i / d}\right) \\ P E_{(p o s, 2 i+1)}=\cos \left(p o s / 10000^{2 i / d}\right) \end{gathered} PE(pos,2i)​=sin(pos/100002i/d)PE(pos,2i+1)​=cos(pos/100002i/d)​
其中， pos 表示单词在句子中的位置， d \mathrm{d} d 表示 PE的维度 (与词 Embedding 一样)，2i 表示偶数的维度， 2 i + 1 2 \mathrm{i}+1 2i+1 表示奇数维度 (即 2 i ≤ d ， 2 i + 1 ≤ d 2 \mathrm{i} \leq \mathrm{d} ， 2 \mathrm{i}+1 \leq \mathrm{d} 2i≤d，2i+1≤d )。使用这种公式计算 P E P E PE 有以下的好处:

  • 使 PE 能够适应比训练集里面所有句子更长的句子，假设训练集里面最长的句子是有 20 个单 词，突然来了一个长度为 21 的句子，则使用公式计算的方法可以计算出第 21 位的 Embedding。
  • 可以让模型容易地计算出相对位置，对于固定长度的间距 k，PE(pos+k) 可以用 PE(pos) 计算 得到。因为

Sin ⁡ ( A + B ) = Sin ⁡ ( A ) Cos ⁡ ( B ) + Cos ⁡ ( A ) Sin ⁡ ( B ) , Cos ⁡ ( A + B ) = Cos ⁡ ( A ) Cos ⁡ ( B ) − \operatorname{Sin}(A+B)=\operatorname{Sin}(A) \operatorname{Cos}(B)+\operatorname{Cos}(A) \operatorname{Sin}(B), \operatorname{Cos}(A+B)=\operatorname{Cos}(A) \operatorname{Cos}(B)- Sin(A+B)=Sin(A)Cos(B)+Cos(A)Sin(B),Cos(A+B)=Cos(A)Cos(B)− $\sin (A) \operatorname{Sin}(B) $

##  PositionalEncoding 代码实现
class PositionalEncoding(nn.Module):
    def __init__(self, d_model, dropout=0.1, max_len=5000):
        super(PositionalEncoding, self).__init__()
 
        ## 位置编码的实现其实很简单，直接对照着公式去敲代码就可以，下面这个代码只是其中一种实现方式；
        ## 从理解来讲，需要注意的就是偶数和奇数在公式上有一个共同部分，我们使用log函数把次方拿下来，方便计算；
        ## pos代表的是单词在句子中的索引，这点需要注意；比如max_len是128个，那么索引就是从0，1，2，...,127
        ##假设我的demodel是512维度，2i那个符号中i从0取到了255，那么2i对应取值就是0,2,4...510
        self.dropout = nn.Dropout(p=dropout)

        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(dim=1)
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)## 这里需要注意的是pe[:, 0::2]这个用法，就是从0开始到最后面，补长为2，其实代表的就是偶数位置
        pe[:, 1::2] = torch.cos(position * div_term)##这里需要注意的是pe[:, 1::2]这个用法，就是从1开始到最后面，补长为2，其实代表的就是奇数位置
        ## 上面代码获取之后得到的pe:[max_len*d_model]
 
        ## 下面这个代码之后，我们得到的pe形状是：[max_len*1*d_model]
        pe = pe.unsqueeze(0).transpose(0, 1)
 
        self.register_buffer('pe', pe)  ## 定一个缓冲区，其实简单理解为这个参数不更新就可以
 
    def forward(self, x):
        """
        x: [seq_len, batch_size, d_model]
        """
        x = x + self.pe[:x.size(0), :]
        return self.dropout(x)

## Encoder 部分包含三个部分：词向量embedding，位置编码部分，注意力层及后续的前馈神经网络
 
class Encoder(nn.Module):
    def __init__(self):
        super(Encoder, self).__init__()
        self.src_emb = nn.Embedding(src_vocab_size, d_model)  ## 这个其实就是去定义生成一个矩阵，大小是 src_vocab_size * d_model
        self.pos_emb = PositionalEncoding(d_model) ## 位置编码情况，这里是固定的正余弦函数，也可以使用类似词向量的nn.Embedding获得一个可以更新学习的位置编码
        self.layers = nn.ModuleList([EncoderLayer() for _ in range(n_layers)]) ## 使用ModuleList对多个encoder进行堆叠，因为后续的encoder并没有使用词向量和位置编码，所以抽离出来；
 
    def forward(self, enc_inputs):
        ## 这里我们的 enc_inputs 形状是： [batch_size x source_len]
 
        ## 下面这个代码通过src_emb，进行索引定位，enc_outputs输出形状是[batch_size, src_len, d_model]
        enc_outputs = self.src_emb(enc_inputs)
 
        ## 这里就是位置编码，把两者相加放入到了这个函数里面，从这里可以去看一下位置编码函数的实现；3.
        enc_outputs = self.pos_emb(enc_outputs.transpose(0, 1)).transpose(0, 1)
 
        ##get_attn_pad_mask是为了得到句子中pad的位置信息，给到模型后面，在计算自注意力和交互注意力的时候去掉pad符号的影响，去看一下这个函数 4.
        enc_self_attn_mask = get_attn_pad_mask(enc_inputs, enc_inputs)
        enc_self_attns = []
        for layer in self.layers:
            ## 去看EncoderLayer 层函数 5.
            enc_outputs, enc_self_attn = layer(enc_outputs, enc_self_attn_mask)
            enc_self_attns.append(enc_self_attn)
        return enc_outputs, enc_self_attns

3. Self-Attention（自注意力机制）

img

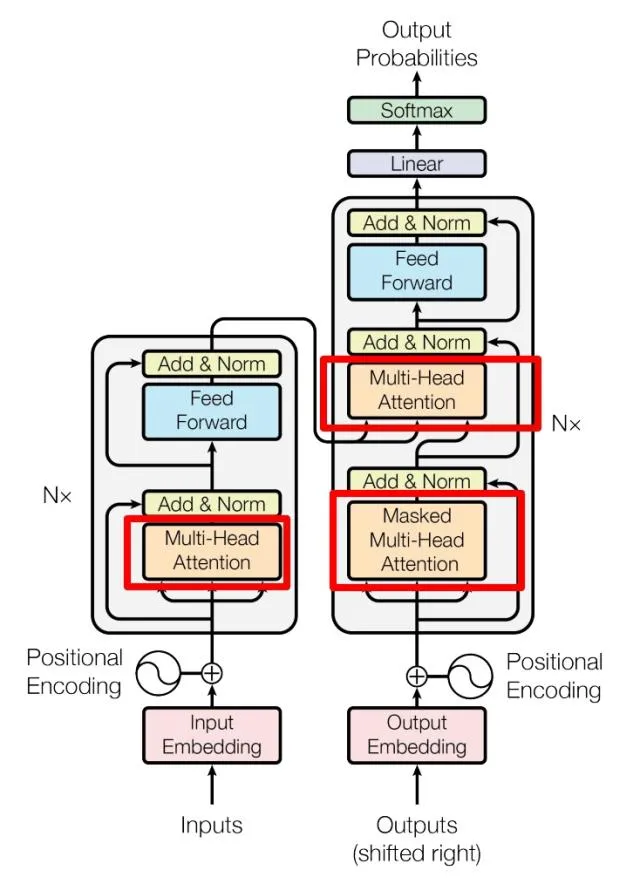
上图是论文中 Transformer 的内部结构图，左侧为 Encoder block，右侧为 Decoder block。红色圈中的部分为 Multi-Head Attention，是由多个 Self-Attention组成的，可以看到 Encoder block 包含一个 Multi-Head Attention，而 Decoder block 包含两个 Multi-Head Attention (其中有一个用到 Masked)。Multi-Head Attention 上方还包括一个 Add & Norm 层，Add 表示残差连接 (Residual Connection) 用于防止网络退化，Norm 表示 Layer Normalization，用于对每一层的激活值进行归一化。

因为 Self-Attention是 Transformer 的重点，所以我们重点关注 Multi-Head Attention 以及 Self-Attention，首先详细了解一下 Self-Attention 的内部逻辑。

3.1 Self-Attention 结构

img

上图是 Self-Attention 的结构，在计算的时候需要用到矩阵Q(查询),K(键值),V(值)。在实际中，Self-Attention 接收的是输入(单词的表示向量x组成的矩阵X) 或者上一个 Encoder block 的输出。而Q,K,V正是通过 Self-Attention 的输入进行线性变换得到的。

3.2 Q, K, V 的计算

Self-Attention 的输入用矩阵X进行表示，则可以使用线性变阵矩阵WQ,WK,WV计算得到Q,K,V。计算如下图所示，注意 X, Q, K, V 的每一行都表示一个单词。

img

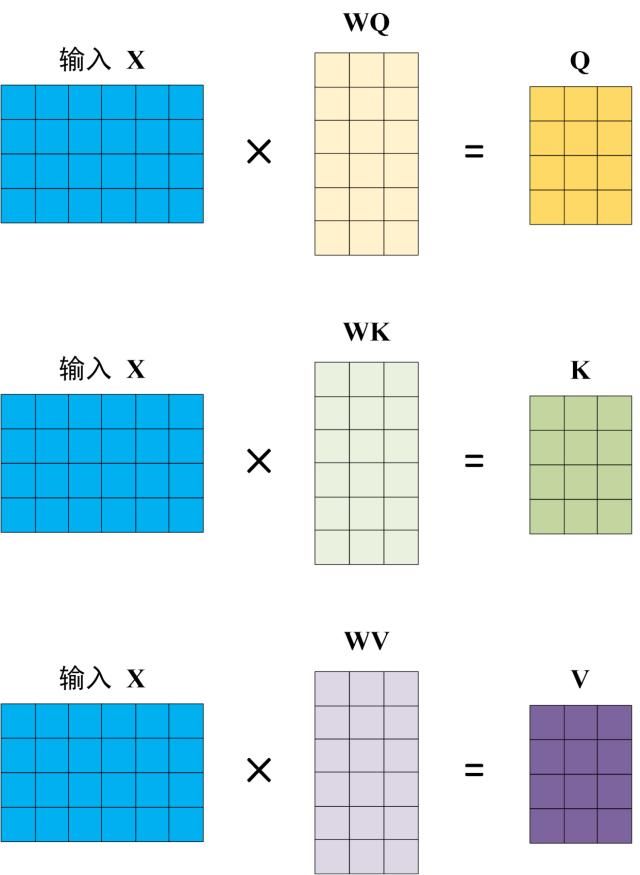
3.3 Self-Attention 的输出

得到矩阵 Q, K, V之后就可以计算出 Self-Attention 的输出了，计算的公式如下：

Attention ⁡ ( Q , K , V ) = softmax ⁡ ( Q K T d k ) V \operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V Attention(Q,K,V)=softmax(dk​ ​QKT​)V d k d_k dk​ 是 Q , K Q, K Q,K 矩阵的列数, 即向量维度
公式中计算矩阵Q和K每一行向量的内积，为了防止内积过大，因此除以 d k d_k dk​ 的平方根，Q乘以K的 转置后，得到的矩阵行列数都为 n , n n, n n,n 为句子单词数，这个矩阵可以表示单词之间的 attention 强
度。下图为Q乘以 K T ， 1234 K^T ， 1234 KT，1234 表示的是句子中的单词。

img

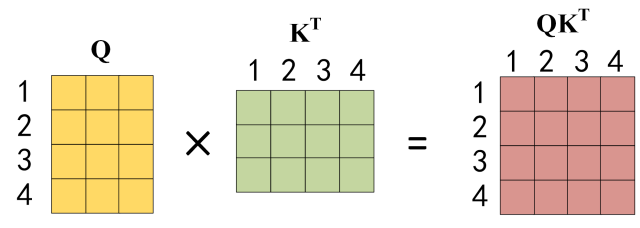
得到 Q K T Q K^T QKT 之后，使用 Softmax 计算每一个单词对于其他单词的 attention 系数，公式中的 Softmax 是对矩阵的每一行进行 Softmax，即每一行的和都变为 1 .

img

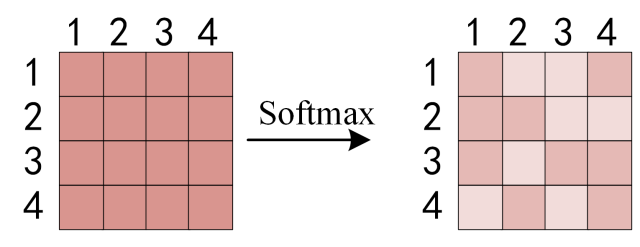
得到 S o f t m a x Softmax Softmax 矩阵之后可以和 V V V相乘，得到最终的输出 Z Z Z。

img

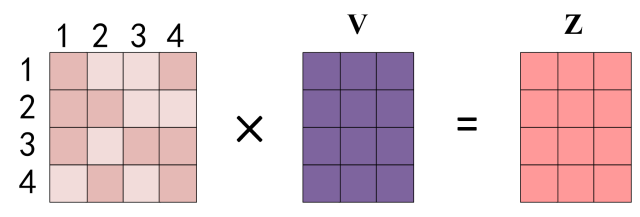
上图中 Softmax 矩阵的第 1 行表示单词 1 与其他所有单词的 attention 系数，最终单词 1 的输出 Z 1 Z_1 Z1​ 等于所有单词 i \mathrm{i} i 的值 V i V_i Vi​ 根据 attention 系数的比例加在一起得到，如下图所示:

img

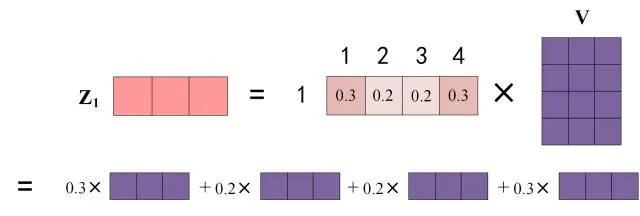
3.4 Multi-Head Attention

在上一步，我们已经知道怎么通过 Self-Attention 计算得到输出矩阵 Z，而 Multi-Head Attention 是由多个 Self-Attention 组合形成的，下图是论文中 Multi-Head Attention 的结构图。

img

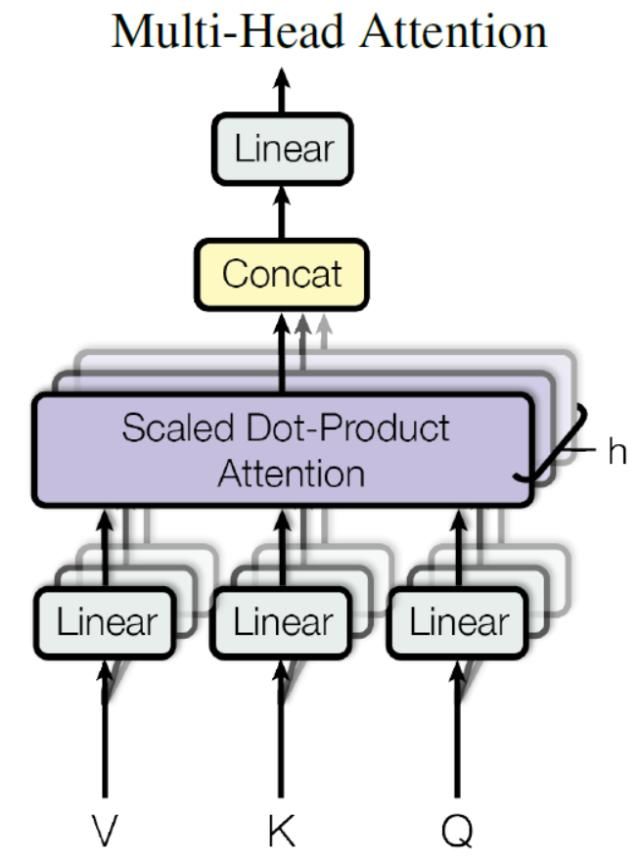
从上图可以看到 M u l t i − H e a d A t t e n t i o n Multi-Head Attention Multi−HeadAttention 包含多个$ Self-Attention$ 层，首先将输入 X X X分别传递到 h \mathrm{h} h 个不同的$ Self-Attention $中，计算得到 h h h 个输出矩阵 Z Z Z。下图是 h = 8 h=8 h=8 时候的情况，此时会得到 8 个输出矩阵Z。

img

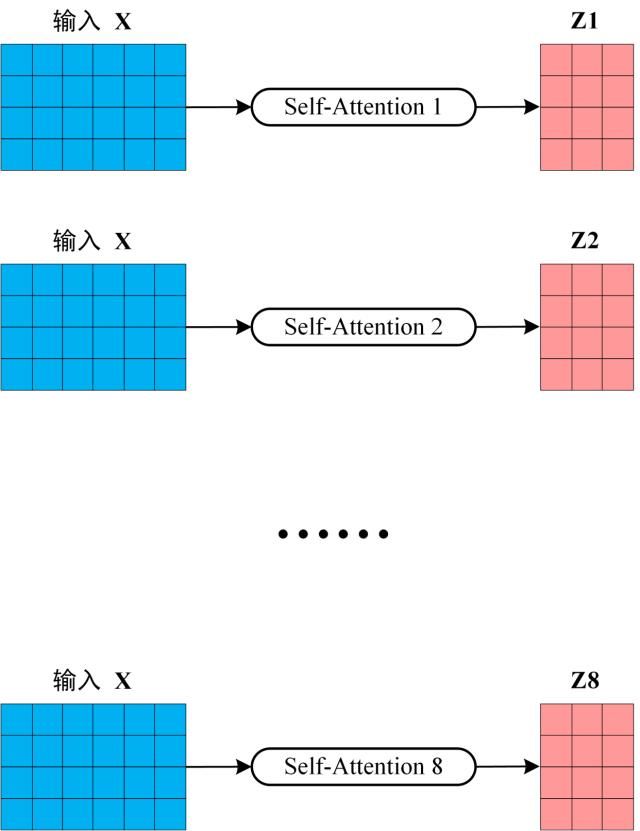
得到 8 个输出矩阵 Z 1 Z_1 Z1​ 到 Z 8 Z_8 Z8​ 之后， M u l t i − H e a d A t t e n t i o n Multi-Head Attention Multi−HeadAttention 将它们拼接在一起$ (Concat) ，然后传入一个 ，然后 传入一个 ，然后传入一个Linear 层，得到 层，得到 层，得到 Multi-Head Attention 最终的输出 最终的输出 最终的输出Z$。

可以看到 Multi-Head Attention 输出的矩阵Z与其输入的矩阵X的维度是一样的。

4. Encoder 结构

img

上图红色部分是$ Transformer $的 $Encoder block 结构，可以看到是由 结构，可以看到是由 结构，可以看到是由 Multi-Head Attention$, A d d & N o r m , F e e d F o r w a r d , A d d & N o r m Add \& Norm, Feed Forward, Add \& Norm Add&Norm,FeedForward,Add&Norm 组成的。刚刚已经了解了$ Multi-Head Attention$ 的计算过程，现在了解一下 A d d & N o r m Add \& Norm Add&Norm 和$ Feed Forward$ 部分。

4.1 Add & Norm

Add & Norm 层由 Add 和 Norm 两部分组成，其计算公式如下:
L a y e r N o r m ( X + M u l t i H e a d A t t e n t i o n ( X ) ) LayerNorm (X+ MultiHeadAttention (X)) LayerNorm(X+MultiHeadAttention(X))

L a y e r N o r m ( X + F e e d F o r w a r d ( X ) ) LayerNorm (X+ FeedForward (X)) LayerNorm(X+FeedForward(X))

其中 X \mathbf{X} X 表示$ Multi-Head Attention$ 或者 $Feed Forward 的输入， 的输入， 的输入，MultiHeadAttention $ ( X ) (\mathbf{X}) (X) 和 FeedForward ( X \mathbf{X} X 表示输出 (输出与输入 X \mathbf{X} X 维度是一样的，所以可以相加)。
Add指 X + \mathbf{X}+ X+ M u l t i H e a d A t t e n t i o n MultiHeadAttention MultiHeadAttention( X ) \mathbf{X}) X) ，是一种残差连接，通常用于解决多层网络训练的问题，可以 让网络只关注当前差异的部分，在 ResNet 中经常用到:

img

Norm指 L a y e r N o r m a l i z a t i o n Layer Normalization LayerNormalization，通常用于 $RNN 结构， 结构， 结构，Layer Normalization$ 会将每一层神经元的输入都转成均值方差都一样的，这样可以加快收敛。

4.2 Feed Forward

Feed Forward 层比较简单，是一个两层的全连接层，第一层的激活函数为 Relu，第二层不使用激活函数，对应的公式如下。
max ⁡ ( 0 , X W 1 + b 1 ) W 2 + b 2 \max \left(0, X W_1+b_1\right) W_2+b_2 max(0,XW1​+b1​)W2​+b2​

X \mathbf{X} X 是输入，Feed Forward 最终得到的输出矩阵的维度与 X \mathbf{X} X 一致。

class FeedForwardNetwork(nn.Module):
    def __init__(self, hidden_size, filter_size, dropout_rate):
        super(FeedForwardNetwork, self).__init__()

        self.layer1 = nn.Linear(hidden_size, filter_size)
        self.relu = nn.ReLU()
        self.dropout = nn.Dropout(dropout_rate)
        self.layer2 = nn.Linear(filter_size, hidden_size)
        initialize_weight(self.layer1)
        initialize_weight(self.layer2)

    def forward(self, x):
        x = self.layer1(x)
        x = self.relu(x)
        x = self.dropout(x)
        x = self.layer2(x)
        return x

4.3 组成 Encoder

通过上面描述的 Multi-Head Attention, Feed Forward, Add & Norm 就可以构造出一个 Encoder block，Encoder block 接收输入矩阵 X ( n × d ) X_{(n \times d)} X(n×d)​ ，并输出一个矩阵 O ( n × d ) O_{(n \times d)} O(n×d)​ 。通过多个 Encoder block 咺加就可以组成 Encoder。
第一个 Encoder block 的输入为句子单词的表示向量矩阵，后续 Encoder block 的输入是前一个 Encoder block 的输出，最后一个 Encoder block 输出的矩阵就是编码信息矩阵 C，这一矩阵后 续会用到 Decoder 中。

img

class Encoder(nn.Module):
    def __init__(self):
        super(Encoder, self).__init__()
        self.src_emb = nn.Embedding(src_vocab_size, d_model)  ## 这个其实就是去定义生成一个矩阵，大小是 src_vocab_size * d_model
        self.pos_emb = PositionalEncoding(d_model) ## 位置编码情况，这里是固定的正余弦函数，也可以使用类似词向量的nn.Embedding获得一个可以更新学习的位置编码
        self.layers = nn.ModuleList([EncoderLayer() for _ in range(n_layers)]) ## 使用ModuleList对多个encoder进行堆叠，因为后续的encoder并没有使用词向量和位置编码，所以抽离出来；
 
    def forward(self, enc_inputs):
        ## 这里我们的 enc_inputs 形状是： [batch_size x source_len]
 
        ## 下面这个代码通过src_emb，进行索引定位，enc_outputs输出形状是[batch_size, src_len, d_model]
        enc_outputs = self.src_emb(enc_inputs)
 
        ## 这里就是位置编码，把两者相加放入到了这个函数里面，从这里可以去看一下位置编码函数的实现；3.
        enc_outputs = self.pos_emb(enc_outputs.transpose(0, 1)).transpose(0, 1)
 
        ##get_attn_pad_mask是为了得到句子中pad的位置信息，给到模型后面，在计算自注意力和交互注意力的时候去掉pad符号的影响，去看一下这个函数 4.
        enc_self_attn_mask = get_attn_pad_mask(enc_inputs, enc_inputs)
        enc_self_attns = []
        for layer in self.layers:
            ## 去看EncoderLayer 层函数 5.
            enc_outputs, enc_self_attn = layer(enc_outputs, enc_self_attn_mask)
            enc_self_attns.append(enc_self_attn)
        return enc_outputs, enc_self_attns

5. Decoder 结构

img

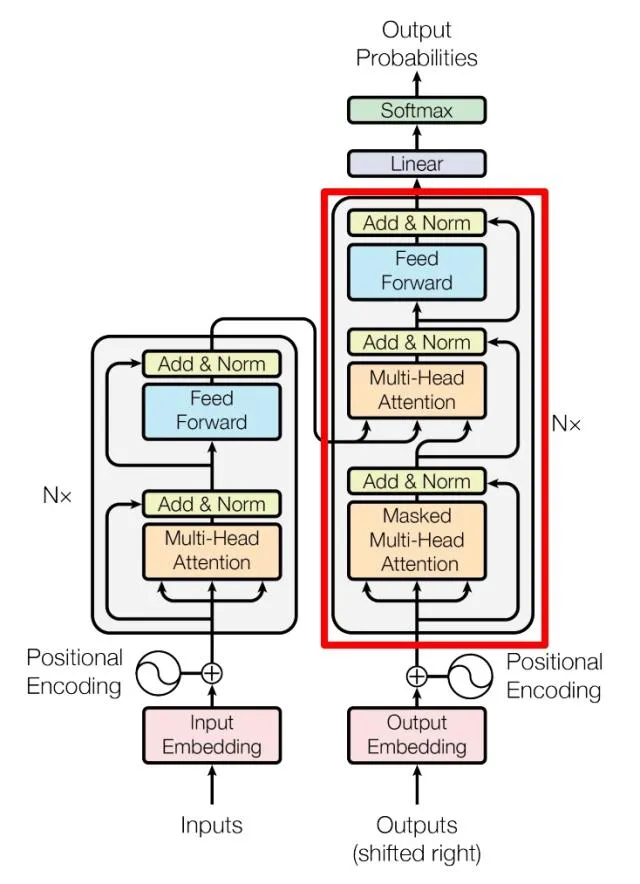
上图红色部分为$ Transformer$ 的$ Decoder block 结构，与 结构，与 结构，与 Encoder block $相似，但是存在一些区别:

  • 包含两个$ Multi-Head Attention$ 层。
  • 第一个 M u l t i − H e a d A t t e n t i o n Multi-Head Attention Multi−HeadAttention 层采用了 $Masked $操作。
  • 第二个$ Multi-Head Attention 层的 层的 层的K, V 矩阵使用 矩阵使用 矩阵使用 Encoder $的编码信息矩阵 C \mathbf{C} C 进行计算，而 Q \mathbf{Q} Q 使 用上一个$ Decoder block $的输出计算。
  • 最后有一个 $Softmax $层计算下一个翻译单词的概率。

完整decoder

class Decoder(nn.Module):
    def __init__(self, hidden_size, filter_size, dropout_rate, n_layers):
        super(Decoder, self).__init__()

        decoders = [DecoderLayer(hidden_size, filter_size, dropout_rate)
                    for _ in range(n_layers)]
        self.layers = nn.ModuleList(decoders)

        self.last_norm = nn.LayerNorm(hidden_size, eps=1e-6)

    def forward(self, targets, enc_output, i_mask, t_self_mask, cache):
        decoder_output = targets
        for i, dec_layer in enumerate(self.layers):
            layer_cache = None
            if cache is not None:
                if i not in cache:
                    cache[i] = {}
                layer_cache = cache[i]
            decoder_output = dec_layer(decoder_output, enc_output,
                                       t_self_mask, i_mask, layer_cache)
        return self.last_norm(decoder_output)

class DecoderLayer(nn.Module):
    def __init__(self, hidden_size, filter_size, dropout_rate):
        super(DecoderLayer, self).__init__()

        self.self_attention_norm = nn.LayerNorm(hidden_size, eps=1e-6)
        self.self_attention = MultiHeadAttention(hidden_size, dropout_rate)
        self.self_attention_dropout = nn.Dropout(dropout_rate)

        self.enc_dec_attention_norm = nn.LayerNorm(hidden_size, eps=1e-6)
        self.enc_dec_attention = MultiHeadAttention(hidden_size, dropout_rate)
        self.enc_dec_attention_dropout = nn.Dropout(dropout_rate)

        self.ffn_norm = nn.LayerNorm(hidden_size, eps=1e-6)
        self.ffn = FeedForwardNetwork(hidden_size, filter_size, dropout_rate)
        self.ffn_dropout = nn.Dropout(dropout_rate)

    def forward(self, x, enc_output, self_mask, i_mask, cache):
        y = self.self_attention_norm(x)
        y = self.self_attention(y, y, y, self_mask)
        y = self.self_attention_dropout(y)
        x = x + y

        if enc_output is not None:
            y = self.enc_dec_attention_norm(x)
            y = self.enc_dec_attention(y, enc_output, enc_output, i_mask,
                                       cache)
            y = self.enc_dec_attention_dropout(y)
            x = x + y

        y = self.ffn_norm(x)
        y = self.ffn(y)
        y = self.ffn_dropout(y)
        x = x + y
        return x

5.1 第一个 Multi-Head Attentionwd

Decoder block 的第一个 Multi-Head Attention 采用了 Masked 操作，因为在翻译的过程中是 顺序翻译的，即翻译完第 i \mathrm{i} i 个单词，才可以翻译第 i + 1 \mathrm{i}+1 i+1 个单词。通过 Masked 操作可以防止第 i \mathrm{i} i 个单词知道 i + 1 i+1 i+1 个单词之后的信息。下面以 “我有一只猫” 翻译成 “I have a cat” 为例，了解一下 Masked 操作。
下面的描述中使用了类似 Teacher Forcing 的概念，不熟悉 Teacher Forcing 的童鞋可以参考以 下上一篇文章Seq2Seq 模型详解。在 Decoder 的时候，是需要根据之前的翻译，求解当前最有可 能的翻译，如下图所示。首先根据输入 “” 预测出第一个单词为 “I”，然后根据输入 " ।" 预测下一个单词 “have”。

img

D e c o d e r Decoder Decoder 可以在训练的过程中使用$ Teacher Forcing $并且并行化训练，即将正确的单词序列 (<Begin > > > I have a cat) 和对应输出 (I have a cat <end > > > ) 传递到 D e c o d e r Decoder Decoder。那么在预测第 i \mathrm{i} i 个 输出时，就要将第 i+1 之后的单词掩盖住，注意 Mask 操作是在$ Self-Attention $的 $Softmax $之 前使用的，下面用 012345 分别表示 “I have a cat ”。

  1. 是 Decoder 的输入矩阵和 Mask 矩阵，输入矩阵包含 “ I have a cat” ( 0 , 1 , 2 (0,1,2 (0,1,2, 3 ，4) 五个单词的表示向量，Mask 是一个 5 × 5 5 \times 5 5×5 的矩阵。在 Mask 可以发现单词 0 只能使用单词 0 的信息，而单词 1 可以使用单词 0,1 的信息，即只能使用之前的信息。

img
输入矩阵与 M a s k 矩阵 输入矩阵与 Mask 矩阵 输入矩阵与Mask矩阵

  1. 接下来的操作和之前的 Self-Attention 一样，通过输入矩阵 X \mathbf{X} X 计算得到 Q K , V \mathbf{Q} \mathbf{K}, \mathbf{V} QK,V 矩阵。然后 计算 Q \mathbf{Q} Q 和 K T K^T KT 的乘积 Q K T Q K^T QKT 。

img
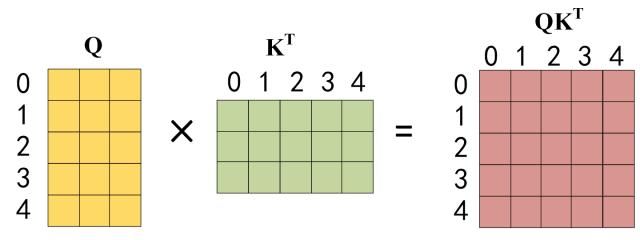
Q 乘以 K 的转置 Q乘以K的转置 Q乘以K的转置

  1. 在得到 Q K T Q K^T QKT 之后需要进行 Softmax，计算 attention score，我们在 Softmax 之前需 要使用Mask矩阵遮挡住每一个单词之后的信息，遮挡操作如下:

img
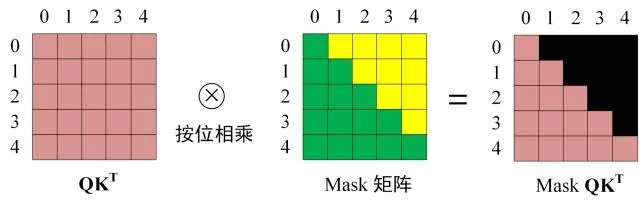
S o f t m a x 之前 M a s k Softmax 之前 Mask Softmax之前Mask
得到 Mask Q K T Q K^T QKT 之后在 Mask Q K T Q K^T QKT 上进行 Softmax，每一行的和都为 1。但是单词 0 在单词 1 ， 2 ， 3 1 ， 2 ， 3 1，2，3 上的 attention score 都为 0 。

  1. 使用 Mask Q K T Q K^T QKT 与矩阵 V \mathbf{V} V 相乘，得到输出 Z \mathbf{Z} Z ，则单词 1 的输出向量 Z 1 Z_1 Z1​ 是只包含单词 1 信息的。

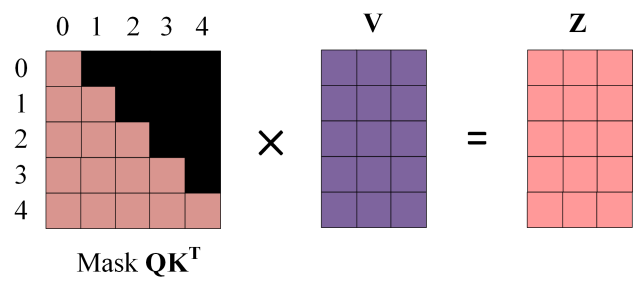
img
M a s k 之后的输出 Mask 之后的输出 Mask之后的输出

  1. 通过上述步骤就可以得到一个$ Mask Self-Attention $的输出矩阵 Z i Z_i Zi​ ，然后和$ Encoder $类似，通过 M u l t i − H e a d A t t e n t i o n Multi-Head Attention Multi−HeadAttention 拼接多个输出 Z i Z_i Zi​ 然后计算得到第一个$ Multi-Head Attention $的输出Z，Z与输入 X \mathbf{X} X 维度一样。
class MultiHeadAttention(nn.Module):
    def __init__(self, hidden_size, dropout_rate, head_size=8):
        super(MultiHeadAttention, self).__init__()

        self.head_size = head_size

        self.att_size = att_size = hidden_size // head_size
        self.scale = att_size ** -0.5

        self.linear_q = nn.Linear(hidden_size, head_size * att_size, bias=False)
        self.linear_k = nn.Linear(hidden_size, head_size * att_size, bias=False)
        self.linear_v = nn.Linear(hidden_size, head_size * att_size, bias=False)
        initialize_weight(self.linear_q)
        initialize_weight(self.linear_k)
        initialize_weight(self.linear_v)

        self.att_dropout = nn.Dropout(dropout_rate)

        self.output_layer = nn.Linear(head_size * att_size, hidden_size,
                                      bias=False)
        initialize_weight(self.output_layer)

    def forward(self, q, k, v, mask, cache=None):
        orig_q_size = q.size()

        d_k = self.att_size
        d_v = self.att_size
        batch_size = q.size(0)

        # head_i = Attention(Q(W^Q)_i, K(W^K)_i, V(W^V)_i)
        # [b,q_len,h,d_k]
        q = self.linear_q(q).view(batch_size, -1, self.head_size, d_k)
        if cache is not None and 'encdec_k' in cache:
            k, v = cache['encdec_k'], cache['encdec_v']
        else:
            k = self.linear_k(k).view(batch_size, -1, self.head_size, d_k)
            v = self.linear_v(v).view(batch_size, -1, self.head_size, d_v)
            if cache is not None:
                cache['encdec_k'], cache['encdec_v'] = k, v

        q = q.transpose(1, 2)                  # [b, h, q_len, d_k]
        v = v.transpose(1, 2)                  # [b, h, v_len, d_v]
        k = k.transpose(1, 2).transpose(2, 3)  # [b, h, d_k, k_len]

        # Scaled Dot-Product Attention.
        # Attention(Q, K, V) = softmax((QK^T)/sqrt(d_k))V
        q.mul_(self.scale)
        x = torch.matmul(q, k)  # [b, h, q_len, k_len]
        x.masked_fill_(mask.unsqueeze(dim=1), -1e9)
        x = torch.softmax(x, dim=3)
        x = self.att_dropout(x)
        x = x.matmul(v)  # [b, h, q_len, attn]

5.2 第二个 Multi-Head Attention

Decoder block 第二个 Multi-Head Attention 变化不大，主要的区别在于其中 Self-Attention 的 K，V矩阵不是使用 上一个 Decoder block 的输出计算的，而是使用 Encoder 的编码信息矩阵 C 计算的。
根据 Encoder 的输出 C计算得到 K , V \mathbf{K}, \mathbf{V} K,V ，根据上一个 Decoder block 的输出 Z \mathbf{Z} Z 计算 Q \mathbf{Q} Q (如果是第 一个 Decoder block 则使用输入矩阵 X \mathbf{X} X 进行计算)，后续的计算方法与之前描述的一致。
这样做的好处是在 Decoder 的时候，每一位单词都可以利用到 Encoder 所有单词的信息 (这些信息无需 Mask)。

5.3 Softmax 预测输出单词

Decoder block 最后的部分是利用 Softmax 预测下一个单词，在之前的网络层我们可以得到一个最终的输出 Z，因为 Mask 的存在，使得单词 0 的输出 Z0 只包含单词 0 的信息，如下：

img
D e c o d e r S o f t m a x 之前的 Z Decoder Softmax 之前的 Z DecoderSoftmax之前的Z

Softmax 根据输出矩阵的每一行预测下一个单词：

img
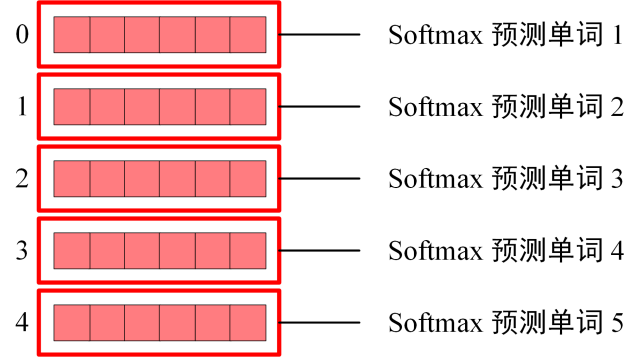
D e c o d e r S o f t m a x 预测 Decoder Softmax 预测 DecoderSoftmax预测
这就是 Decoder block 的定义，与 Encoder 一样，Decoder 是由多个 Decoder block 组合而成。

6.Transformer 总结

  • Transformer 与 RNN 不同，可以比较好地并行训练。
  • Transformer 本身是不能利用单词的顺序信息的，因此需要在输入中添加位置 Embedding，否 则 Transformer 就是一个词袋模型了。
  • Transformer 的重点是 Self-Attention 结构，其中用到的 Q , K , V \mathbf{Q}, \mathbf{K}, \mathbf{V} Q,K,V 矩阵通过输出进行线性变换得 到。
  • Transformer 中 Multi-Head Attention 中有多个 Self-Attention，可以捕获单词之间多种维度 上的相关系数 attention score。

参考

  1. Attention Is All You Need
  2. Transformer模型详解（图解最完整版）

相关文章：

  • 做徽标的网站/属于b2b的网站有哪些
  • 网站开发心得体会/搜狗推广管家
  • 阳江网站开发/网络营销的六个特点
  • 凡科网上传网站/成人大专
  • 贵阳网站开发工作室/网络营销主要是什么
  • 网站建设服务费标准/seo综合查询
  • Eclipse 连接 SQL Server 数据库教程
  • 实时更新的github hosts地址
  • 一周技术学习笔记(第97期)-掌握DDD不是想象的那么容易吗？
  • 计算机基础（六）：静态链接与动态链接
  • Tslib配置文件ts.conf
  • 2023年1月16日--2023年1月22日（osg+glsl+socket+ue）
  • 人类从未如此需要知识 知识从未如此昂贵
  • SpringCache之@CachePut注解的使用说明
  • 2022年，开源社最亮的星
  • 来看看我在CSDN上的好朋友们吧，看看有没有你
  • TreeMap 原理实现及常用方法
  • golang实现大顶堆只看这篇文章就够了