机器学习的几个公式
今天看了几个公式的推演过程,有些推演过程还不是很明白,再着担心自己后面会忘记,特来此记下笔记。python 是由自己特定的公式符号的,但推演过程需要掌握,其实过程不过程不是重点,只要是要记得公式的含义,以便符合业务场景需求。
均值
向量的模
欧式距离
余弦相似度
方差
协方差
相关系数
将公式之前,先把numpy和数据引入下。示例是以sklearn.datasets 中鸢尾花数据做示例。
#加载numpy和数据
import numpy as np
from sklearn.datasets import load_iris
#加载数据
X,y = load_iris(return_X_y=True)
- 均值
均值用的比较多,也是相对简单的计算公式,也就是总数除以总个数.
X0 = X[0,:] #取特征数据第一行
X1 = X[1,:]#取特征数据第二行
求X0的平均值:
算法推演写法:
X0.sum()/X0.size
换成python--nupmy公式写法为:
X0.mean()
下面截图是在python上运行的结果
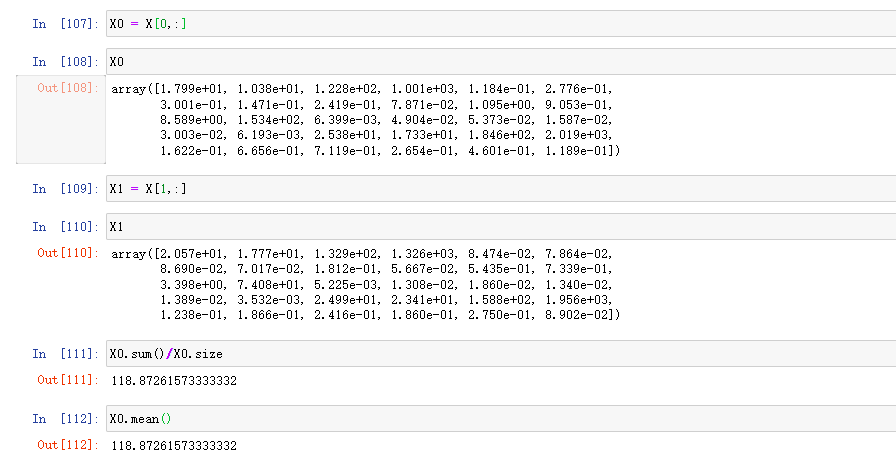
- 向量的模
求X0的向量的模:
算法推演写法:
np.sqrt((X0**2).sum())
换成python--nupmy公式写法为:
np.linalg.norm(X0)
下面是python运行结果
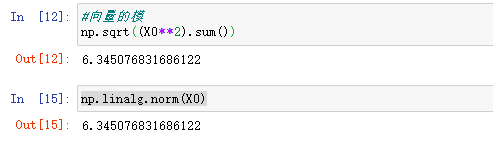
- 欧式距离

欧式距离是两点之间的直线距离。以上面的X0,X1为例。欧式距离其实是向量的模的扩展版,都是运用勾股定理,只不过向量的一个点假定为原点,所以不用计算,直接求出。而欧式距离需要相减后平方再相加,最后开根号。
求X0 ,X1的直线距离
推演写法:
np.sqrt(((X0-X1)**2).sum())
换成python--nupmy公式写法为:
np.linalg.norm(X0-X1) #公式都是一样的,只不过参数从X0,换成X0-X1
- 余弦相似度
余弦也就是我们中学时候接触得cos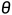 ,求得是两个变量之间得夹角大小。
,求得是两个变量之间得夹角大小。

以X0,X1为例:
cos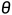 = X0 * X1 / |X0| / |X1|
= X0 * X1 / |X0| / |X1|
要求出他们得余弦相似度,需要先求出两者得模。用两者的乘积 除以两者各自的模
求X0 ,X1的余弦相似度
推演写法:
(X0 * X1 ).sum()/ (np.sqrt(X0**2).sum())) / (np.sqrt(X1**2).sum()))
换成python--nupmy公式写法为:
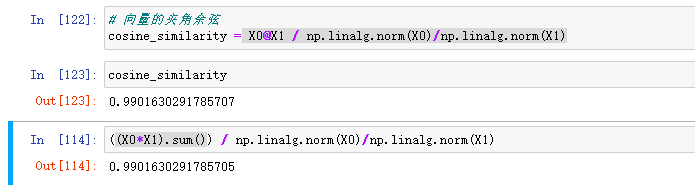
X0@X1 / np.linalg.norm(X0) / np.linalg.norm(X1)
下面是python的运行结果
- 方差
方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中,研究方差即偏离程度有着重要意义。【百度百科】

这里多说一些,方差分”有偏统计“和”无偏统计“。定义:
拿一个样本的统计量,评估出来的结果再取一个期望值,这个期望值等于真实结果就是“无偏统计”,不等于真实结果就是”有偏统计“。无偏统计除以(n-1),”有偏统计“除以n。这是科学上的理论知识,有兴趣的同学可自行深入了解,但工程上的数据量往往比较大,减一不减一差别不大。所以一般不用理会。
求X0 的方差
推演写法:
(X0 - X0.mean() )**2/ X0.size
换成python--nupmy公式写法为:
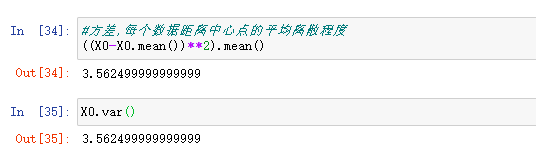
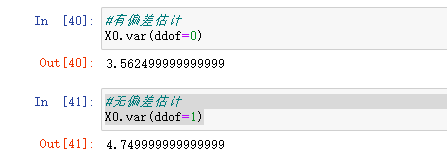
X0.var() #默认ddof = 0,也就是有偏差统计
X0.var(ddof = 1) #设置成无偏差统计
下面的python运行结果
- 协方差
方差是考察一列数据的离散程度,而协方差是考察两列数据的离散程度。
协方差(Covariance)在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
协方差表示的是两个变量的总体的误差,这与只表示一个变量误差的方差不同。如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。【百度百科】

求X0、X1 的协方差
推演写法:
(X0 - X0.mean() ) *(X1-X1.mean())/X0.size #X0,X1的size(形状)是一样大的
或:X0 - X0.mean() ) *(X1-X1.mean()).mean()
换成python--nupmy公式写法为:
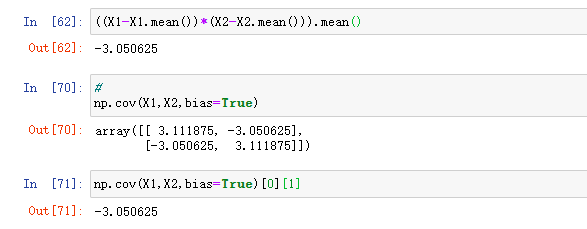
X0.cov()[0][1]
或X0.cov()[1][0] #主要是两个数列的离散程度, 0-0,1-1都是一个数列的X0,X1自己离散程度
下面是python运行结果
- 相关系数
相关系数是最早由统计学家卡尔·皮尔逊设计的统计指标,是研究变量之间线性相关程度的量。
简单理解就是把上面的协方差结果缩放到-1 ~1之间。这样更容易看出两者的相关系统。

求X0、X1 的相关系数
推演写法:
首先先求协方差:
(X0 -X0.mean()) * (X1-X1.mean()).mean()
然后求X0 与X1 的方差
X0: ((X0-X0.mean)**2).mean()
X1: ((X1-X1.mean)**2).mean()
最后求整体: (X0 -X0.mean()) * (X1-X1.mean()).mean() /np.sqrt( ((X0-X0.mean)**2).mean()* ((X1-X1.mean)**2).mean())
换成python--nupmy公式写法为:
np.corrcoef(X0,X1)[0][1]
下面是python运行效果

