1. 协方差

标准差和方差一般是用来描述一维数据的，

具体介绍见：5. 统计学基础1：平均值…四分位数、方差、标准差（均方差）、标准误（标准误差、均方根误差）、 标准分

但现实生活中我们常常会遇到含有多维数据的数据集，最简单的是大家上学时免不了要统计多个学科的考试成绩。
面对这样的数据集，我们当然可以按照每一维独立的计算其方差，但是通常我们还想了解更多，
比如，一个男孩子的猥琐程度跟他受女孩子的欢迎程度是否存在一些联系。
协方差就是这样用来度量两个随机变量关系的统计量
我们可以仿照方差的定义：

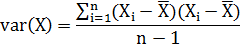
来度量各个维度偏离其均值的程度，协方差可以这样来定义：

协方差的结果有什么意义呢？
如果X 变大时 Y 也变大，则协方差为正值，则说明两者是正相关，也就是说一个人越猥琐，越受女孩欢迎。
如果X 变大时 Y 变小，则协方差为负值，就说明两者是负相关，越猥琐，女孩子越讨厌。
如果为0或者接近0，则认为是没有线性关系的，就是统计上说的“相互独立”。

我们可以根据协方差的这种协同性来判断数据在不同“方向”上的离散程度。

从协方差的定义上，我们也可以看出一些显而易见的性质，如：

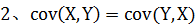
2. 相关系数【就是使 |协方差|<=1】

协方差的值的大小除了两种变量的相关性有关外，还与变量的量纲有关。
如果 X 是以10为量纲，而 Y 以10万为量纲，而 Z也是以10为量纲。
假设 X 与 Z 之间具有很强的相关性（比如 X _i = Z _i ），而 X、Y 之间不具有很强的相关性，
应满足X与Z的相关系数 要大于 X与Y的相关系数
但是由于量纲的影响，实际上是小于

为了消除量纲的影响，引入了相关系数，可以使 |协方差| <=1

为了能够更好地衡量变量之间的相关程度，引入了相关系数 η

D(x)为x的方差，sqrt(D(x))为x的标准差
由不等式知：分母>=分子，故|η|<=1

因此， η 的取值范围为 [ − 1 , 1 ]
当 η 为正值时，X、Y 正相关，值越大正相关性越强；
当 η 为负值时，X 、Y负相关，值越小负相关性越强
当 η 趋于 0 时，基本不相关。当 η = 0 时， X、Y 不相关。

注 ：此处所说的相关性都是线性相关性，有可能两者之间存在非线性的相关性

3. 协方差矩阵

前面提到的猥琐和受欢迎的问题是典型的二维问题，而协方差也只能处理二维问题，
那维数多了自然就需要计算多个协方差，于是就有了协方差矩阵