如何实现六轴机械臂的逆解计算?
1. 机械臂运动学介绍
机械臂运动学
机器人运动学就是根据末端执行器与所选参考坐标系之间的几何关系,确定末端执行器的空间位置和姿态与各关节变量之间的数学关系。包括正运动学(Forward Kinematics)和逆运动学(Inverse Kinematics)两部分。
正运动学就是根据给定的机器人的各个关节变量,计算末端执行器的位置和姿态,也被称为机器人运动学建模。
逆运动学则是根据已知的末端执行器的位置和姿态,计算机器人各个关节变量,也被称为机器人运动学求解。
关节变量 —–> 机械臂末端执行器的姿势 = 正向运动学
机械臂末端执行器的位姿 —–> 关节变量 = 逆向运动学
逆运动学的求解方法有两类:
(1)解析解法
① 代数法
② 几何法
(2)数值解法
① 迭代法
② 优化法
2. 逆向运动学解算思路
初始坐标系

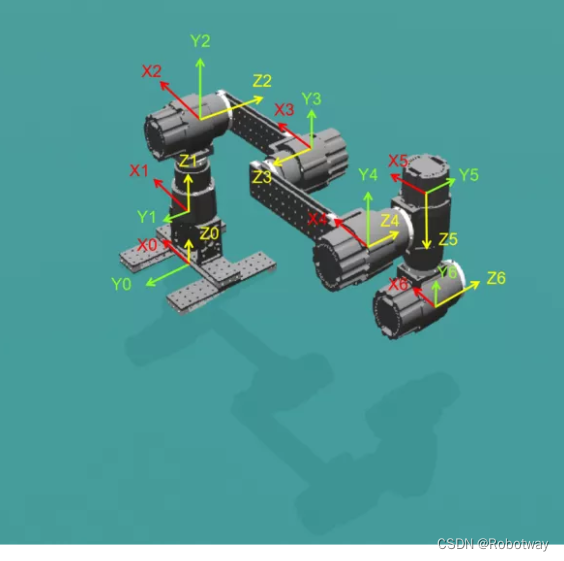
解算顺序为:θ1、θ5、θ6、θ3、计算θ2、计算θ4。
2.1 解算θ1


(1)机械臂初始状态坐标系(如下图所示)

(2)将关节1转动θ1,转动后的关节坐标系如下图所示:
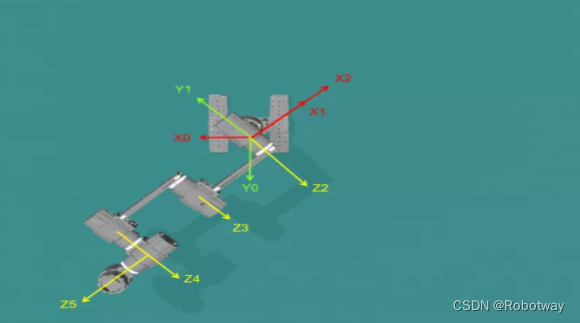
将机械臂模型简化

计算过程:

用代码表示:

2.2 解算θ5
将关节5转动θ5后的关节坐标系如下图所示(图中Z5应为穿过关节5中心,垂直向下指向地面的轴):

将机械臂模型简化

计算过程:

用代码表示:
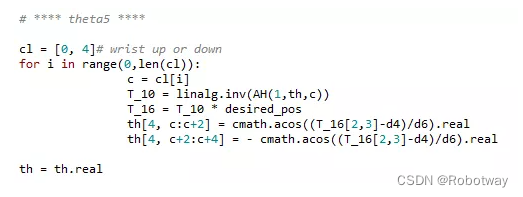
2.3 解算θ6
(1)机械臂初始的关节坐标系(如下图所示)

(2)将机械臂模型简化,并确定θ6方向

(3)将关节6转动-θ6


(4)将末端抽象为球坐标系

(5)计算过程:

(6)用代码表示:
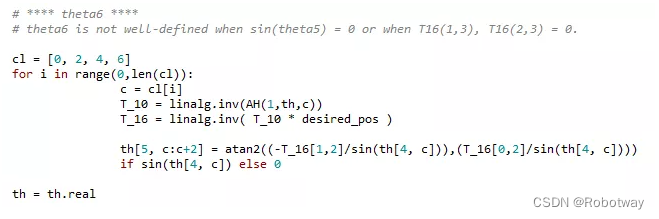
2.4 解算θ3
(1)机械臂初始姿态如下图所示:

(2)将关节2转动 θ2,将关节3转动-θ3

(3)将机械臂模型简化,并注意初始位置
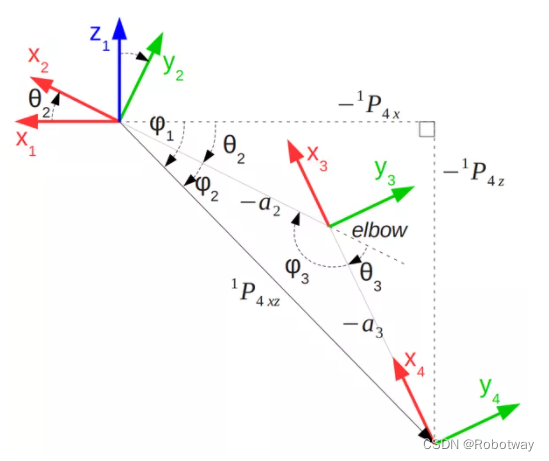
(4)计算过程:

(5)用代码表示:

2.5 解算θ2
(1)模型不变

(2)计算过程

(3)用代码表示

2.6 解算θ4
(1)提取θ4所在关节模型

(2)计算过程

(3)用代码表示

以上计算方法和过程,可以基于Webots构建出来,了解详情请观看视频或下载资料。
讲解视频1:2022.06.08六轴机械臂正逆解计算及仿真实例(下)
讲解视频2:全程干货【六轴机械臂正逆解计算及仿真示例】
3.资料内容
① 六轴机械臂正逆运动学讲解.pptx
② 仿真项目源代码
③ 电机驱动函数库
资料内容下载详见 如何实现机械臂的逆解计算
