这篇讲一下前缀和与差分数组的关系

1. 前缀和

1.1 一维数组前缀和

前缀和在处理数组中的连续子数组的某一段加和的问题中很有用, 因为是拿空间换时间, 可以将线性复杂度降低为常数时间复杂度.

前缀和的道理很简单, 对于数组$arr[i],i=0,...,n-1$, 我们按照如下关系定义前缀和数组$preSum[i]$:

$$preSum[i]=preSum[i-1]+arr[i-1],i=1,...,n$$

这时, $preSum[i]$表示的是$arr$数组前$i$个的元素和, $preSum$的长度为$n+1$. 在这种情况下, 定义$preSum[0]=0$(因为前0个元素的和没有定义). 这样, 如果我们要计算$arr[l]+arr[l+1]+...+arr[r]$的和, 那么显然可以用前$r+1$个元素的和减去前$l$个元素的和决定, 也就有:

$$arr[l]+arr[l+1]+...+arr[r]=preSum[r+1]-preSum[l]$$

当然, 我们也可以按照如下方式定义:

$$\begin{gathered} preSum[0]=arr[0] \\ preSum[i]=preSum[i-1]+arr[i],i=1,...,n-1 \end{gathered}$$

如果按照这种方式定义, 则$preSum[i]$的意义就更简单: 即$arr[0]+...+arr[i]$, 也就是前$i+1$项的和. 这样的话, $preSum$的长度与$arr$的一致, 都为$n$. 这样, 如果我们要计算$arr[l]+arr[l+1]+...+arr[r]$的和, 有:

$$arr[l]+arr[l+1]+...+arr[r]=preSum[r]-preSum[l]$$

两种方式都差不多, 第一种具有更好的公式一致性.

下面用例题来展示一下一维前缀和的应用.

1.1.1 长度最小的子数组

这是一个经典的基本的前缀和问题. 题目要求求解最短的连续子序列, 使得子序列的和大于等于目标值.

我们可以很容易地想到用前缀和快速在$O(1)$的复杂度内计算某个区间的和. 为了求出最短的子序列, 我们对前缀和数组枚举左右端点, 也就是滑动窗口的方法. 对于每一个右端点, 枚举左端点, 只要合法(和大于target), 那么就右移左端点, 并更新答案即可. 整体的复杂度为$O(n)$.

代码:

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int length = nums.size();
        vector<int> preSum (length + 1, 0);  // preSum[i] 前i个元素的和
        int result = INT_MAX;

        for (int idx = 0; idx < length; idx ++)
            preSum[idx + 1] = preSum[idx] + nums[idx];

        // 找到最小的j - i使得preSum[j + 1] - preSum[i] >= target
        // 用滑动窗口
        int left = 0, right = 1;
        while (right < length + 1) {
            // 对于每个right 找到尽量靠近right 的left
            while (preSum[right] - preSum[left] >= target) {
                result = min(result, right - left);
                left ++;
            }
            right ++;
        }

        return result == INT_MAX ? 0 : result;
    }
};

1.1.2 除自身以外数组的乘积

这个题让我们返回一个新数组, 新数组的每个元素表示的是元素组除了对应索引外的这个元素其余元素的乘积. 我们可以借鉴前缀和的思想, 对于原数组的第i个元素, 除它之外的乘积是前i个元素的积, 与后length - (i + 1)个元素的积. 因此我们定义两个前缀数组, 一个left表示从前面数元素的累积, 一个right表示从后面数元素的累积, 最后第i个元素, 除它之外的乘积是left[i] * right[length - (i + 1)]:

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int length = nums.size();
        // 用两个数组记录前缀乘积与后缀乘积 则
        // nums[i]对应答案为preMulLeft[i] * preMulRight[length - 1 - i]
        vector<int> preMulLeft (length + 1, 1);  // 前i个元素的乘积
        vector<int> preMulRight (length + 1, 1);  // 后i个元素的乘积

        for (int idx = 0; idx < length; idx ++) 
            preMulLeft[idx + 1] = preMulLeft[idx] * nums[idx];
        for (int idx = 0; idx < length; idx ++) 
            preMulRight[idx + 1] = preMulRight[idx] * nums[length - 1 - idx];

    
        vector<int> result (length, 1);
        for (int idx = 0; idx < length; idx ++)
            result[idx] = preMulLeft[idx] * preMulRight[length - 1 - idx];

        return result; 

    }
};

1.2 二维数组前缀和

二维数组前缀和与一维的一致, 只需要理解下面的图就可以了:

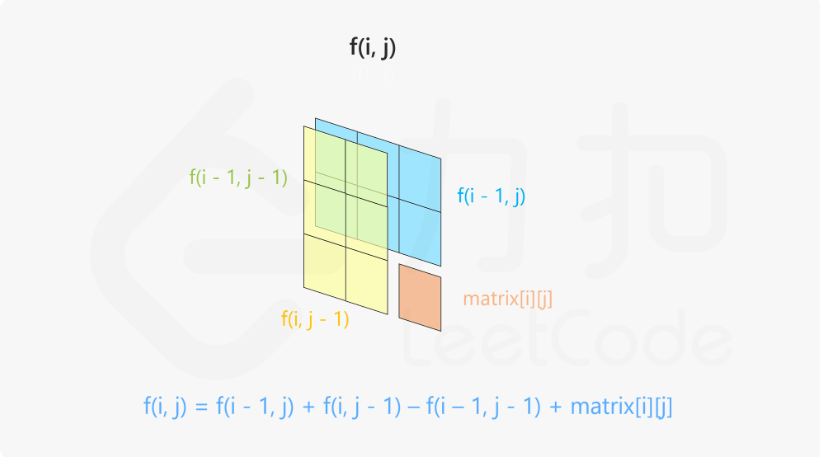
也就是说, 二维数组的某处i, j的前缀和是i, j - 1处的(黄色部分)加上i - 1, j处的(蓝色部分)减去i-1, j-1处的(黄色与蓝色重叠部分)再加上对应元素值的即可.
如果我们采用第一种方式定义, 即$preSum[i][j]$表示前$i$行前$j$列所有元素的和, 那么有如下关系:

$$preSum[i][j]=preSum[i-1][j]+preSum[i][j-1]-preSum[i-1][j-1]+arr[i-1][j-1],i,j=1,...,n$$

1.2.1 二维区域和检索 - 矩阵不可变

这个题让我们返回某个子矩阵的元素和. 可以利用上面的二维前缀和来做, 代码如下:

class NumMatrix {
public:
    vector<vector<int>> sums;

    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size();
        if (m > 0) {
            int n = matrix[0].size();
            sums.resize(m + 1, vector<int>(n + 1));
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    sums[i + 1][j + 1] = sums[i][j + 1] + sums[i + 1][j] - sums[i][j] + matrix[i][j];
                }
            }
        }
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        return sums[row2 + 1][col2 + 1] - sums[row1][col2 + 1] - sums[row2 + 1][col1] + sums[row1][col1];
    }
};

2. 差分数组

差分可以看作是前缀和的逆运算(相当于积分与求导的关系). 为了便于理解, 对于数组$arr[i],i=0,...,n-1$, 按照如下方式定义差分数组$diff$:

$$\begin{gathered} diff[0]=arr[0] \\ diff[i]=arr[i]-arr[i-1],i=1,...,n-1 \end{gathered}$$

我们对差分数组求前缀和, 按照第二种前缀和定义的方式(这样差分数组与前缀和数组长度都为$n$, 便于理解), 结果恰为原数组. 例如:

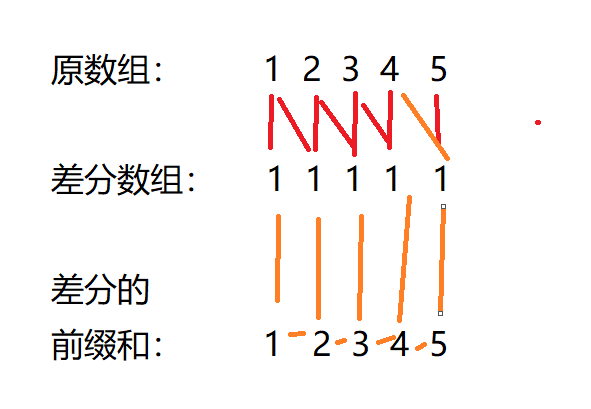
差分数组可以干什么呢? 如果我们想批量对某个区间进行加减, 则是很有用的. 例如, 我要对数组1,2,3,4,5的3,4都加1, 那么可以将差分数组3对应的位置加1, 5对应的位置减1, 如下图:

简单来讲, 如果想对数组的[l, r]区间(闭区间)同时加r, 则等效于将diff[l] += r, diff[r + 1] -= r, 再求diff的前缀和. 为了不让数组越界, 防止r为右端点的情形, 我们可以多开一个元素.

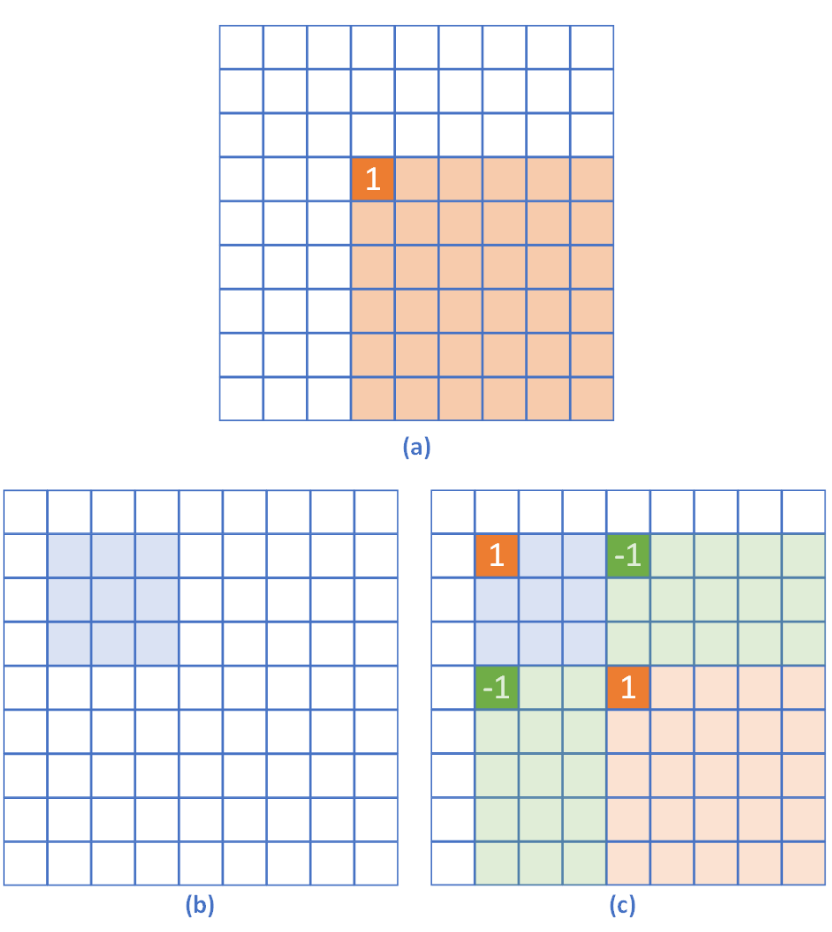
二维的差分也是一样的道理, 如果想对[x1, y1]到[x2, y2]都加r, 则等效于做一下操作:

diff[x1][y1] += r
diff[x1 + 1][y1] -= r
diff[x1][y1 + 1] -= r
diff[x1 + 1][y1 + 1] += r

按照下图就好理解了:(牢记要对差分数组求前缀和)(图的来源: LeetCode题解)

有了以上的基础, 可以很容易做出来下面的题了:

子矩阵元素加 1

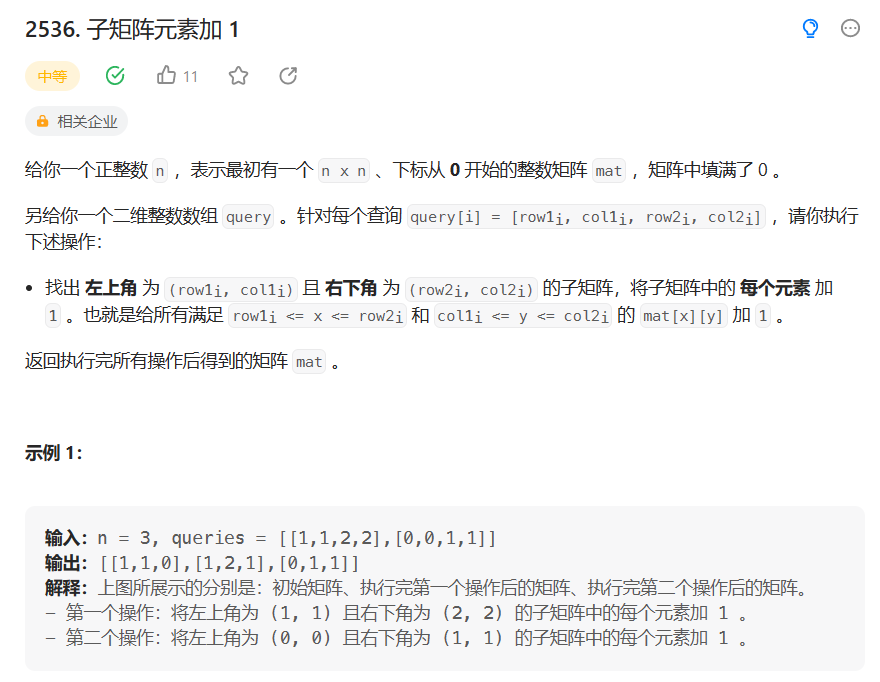
代码:

class Solution {
public:
    vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
        vector<vector<int>> result (n, vector<int> (n, 0));  // 结果数组
        vector<vector<int>> diff (n + 1, vector<int> (n + 1, 0));  // 差分数组
        // 因为可能对边界操作 故多开一个

        // 计算出差分数组 再对差分数组求前缀和就是结果
        for (auto& q : queries) {
            int row0 = q[0], row1 = q[2], col0 = q[1], col1 = q[3];

            diff[row0][col0] += 1;
            diff[row1 + 1][col0] -= 1;
            diff[row0][col1 + 1] -= 1;
            diff[row1 + 1][col1 + 1] += 1;
        }

        // result 即为diff的前缀和
        // 先将左上角与边缘的计算出来
        result[0][0] = diff[0][0];
        for (int i = 1; i < n; i ++) {
            result[0][i] = result[0][i - 1] + diff[0][i];
            result[i][0] = result[i - 1][0] + diff[i][0];
        }

        // 其余位置 二维前缀和
        for (int row = 1; row < n; row ++) {
            for (int col = 1; col < n; col ++) 
                result[row][col] = result[row - 1][col] + result[row][col - 1] - result[row - 1][col - 1] + diff[row][col];
        }

        return result;

    }
};