图解二叉树的构造 | 中序 + 后序
中序后续构造二叉树
https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/
递归思路
递归思路很简单, 因为无论是构造一棵大树还是一棵小树, 都是重复的子问题, 思路主要麻烦在边界上
如下图所示
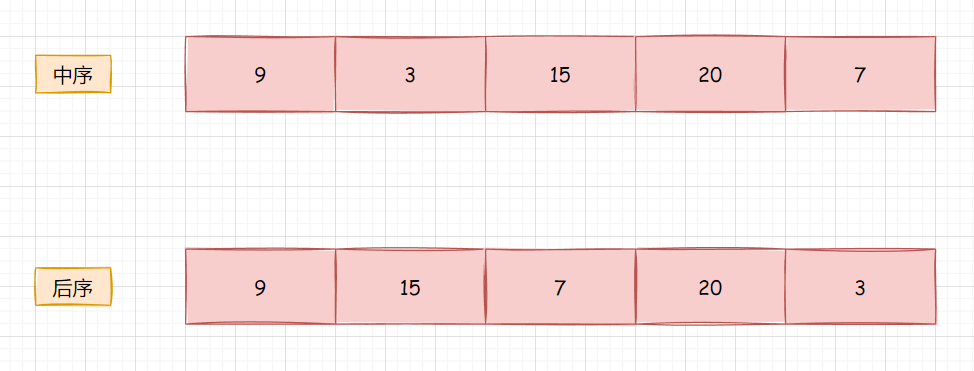
上述是中序和后续序列
我们要递归, 需要首先确定递归函数, 因为题目是以数组形式, 我们如果要取数据, 需要开始和结束下标, 所以递归函数的下标是
public TreeNode buildTree(int[] inorder, int inStart, int inEnd,int[] postorder, int postStart, int postEnd)
下一步是终止条件, 因为是给定了下标, 如果下标不合法, 说明到达终止条件, 因为递归的话, 需要不断去划分左右子树
if(inStart > inEnd) {
return null;
}
最后是当前层的执行逻辑 :
- 构造根节点
- 构造左子树和右子树
- 获取左子树的中序和后续数组开始和结束下标
- 获取右子树的中序和后续数组开始和结束下标

麻烦的就是下标边界问题, 很容易写错, 其实也很简单 :

如上图 :
- 中序的下标很好判断, 只要找到根节点的下标即可
- 后序的话, 因为是左右根的节点顺序, 所以计算出 leftsize , 也就是左子树的节点数, 就可以计算出新的左子树
- 计算 leftSize = rootValIndex - inStart 这个结果其实就是计算 rootValIndex 向左走 leftSize 步
- inStart + leftSize 等于初始位置向右移动 leftSize 步
// 1. 获取根节点的值
int rootVal = postorder[postEnd];
// 2. 获取根节点在中序的下标
int rootValIndex = valueToIdx.get(rootVal);
// 计算左子树的大小
// [1,2, {3}, 4,5,6]
// 中值是 3 : leftSize = 2 - 0 = 2
// rightSize = 5 - 2 = 3
int leftSize = rootValIndex - inStart;
// 新的中序开始/结束下标
// 左子树
int newLeftInStart = inStart;
int newLeftInEnd = rootValIndex - 1;
// 右子树
int newRightInStart = rootValIndex + 1;
int newRightInEnd = inEnd;
// 新的后序开始/结束下标
// 左子树
int newLeftPostStart = postStart;
int newLeftPostEnd = postStart + leftSize - 1;
// 右子树
int newRightPostStart = postStart + leftSize;
int newRightPostEnd = postEnd - 1;
递归代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private Map<Integer, Integer> valueToIdx = new HashMap<>();
public TreeNode buildTree(int[] inorder, int inStart, int inEnd,
int[] postorder, int postStart, int postEnd){
if(inStart > inEnd) {
return null;
}
// 1. 获取根节点的值
int rootVal = postorder[postEnd];
// 2. 获取根节点在中序的下标
int rootValIndex = valueToIdx.get(rootVal);
// 计算左子树的大小
// [1,2, {3}, 4,5,6]
// 中值是 3 : leftSize = 2 - 0 = 2
// rightSize = 5 - 2 = 3
int leftSize = rootValIndex - inStart;
// 新的中序开始/结束下标
// 左子树
int newLeftInStart = inStart;
int newLeftInEnd = rootValIndex - 1;
// 右子树
int newRightInStart = rootValIndex + 1;
int newRightInEnd = inEnd;
// 新的后序开始/结束下标
// 左子树
int newLeftPostStart = postStart;
int newLeftPostEnd = postStart + leftSize - 1;
// 右子树
int newRightPostStart = postStart + leftSize;
int newRightPostEnd = postEnd - 1;
TreeNode root = new TreeNode(rootVal);
root.left = buildTree(
inorder, newLeftInStart, newLeftInEnd,
postorder, newLeftPostStart, newLeftPostEnd
);
root.right = buildTree(
inorder, newRightInStart, newRightInEnd,
postorder, newRightPostStart, newRightPostEnd
);
return root;
}
public TreeNode buildTree(int[] inorder, int[] postorder) {
for(int i = 0 ; i < inorder.length ; i++) {
valueToIdx.put(inorder[i], i);
}
return buildTree(
inorder, 0, inorder.length - 1,
postorder, 0, postorder.length - 1
);
}
}
