顺序表仅适用于不常进行插人和删除的线性表。因为在顺序存储表示的线性表中插入或删除一个数据元素,平均约需移动表中一半元素,这个缺陷是由于顺序存储要求线性表的元素依次“紧挨”存放造成的。因此对于经常需要进行插人和删除操作的线性表,就需要选择其他的存储表示方法。现在我们讨论线性表的另一种表示方法——链式存储表示,由于它不要求逻辑上“相邻”(例如ai和ai+1)的两个数据元素在存储位置上也“相邻”,因此它没有顺序存储结构所具有的弱点,但同时也失去了顺序表可随机存取的优点。

一、单链表和指针

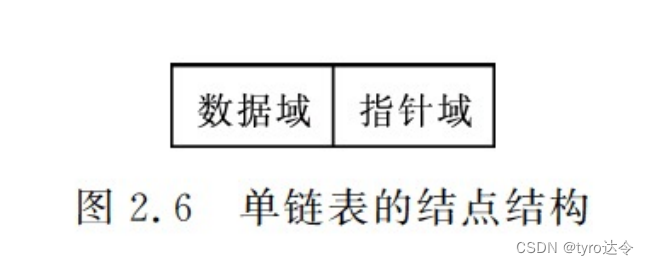
线性表的链式存储表示的特点是用一组任意的存储单元存储线性表的数据元素(这组存储单元可以是连续的,也可以是不连续的)。因此,为了表示每个数据元素 ai与其直接后继数据元素 a i+1之间的逻辑关系,对数据元素 ai来说,除了存储其本身的信息之外,还需存储一个指示其直接后继的信息(即直接后继的存储位置)。这两部分信息组成一个“结点”表示线性表中一个数据元素 ai。结点中存储数据元素信息的域称为数据域(设域名为data),存储直接后继存储位置的域称为指针域(设域名为 next)。指针域中存储的信息又称做指针或链。上述结点结构如图 2.6 所示。N 个结点(分别表示 a1,a2, ..... ,an)依次相链构成一个链表,称为线性表的链式存储表示,由于此类链表的每个结点中只包含一个指针域,故又称单链表或线性链表。

例如图 2.7 所示为线性表

(ZHAO，QIAN，SUN，LI, ZHOU，WU，ZHENG，WANG) 的单链表。

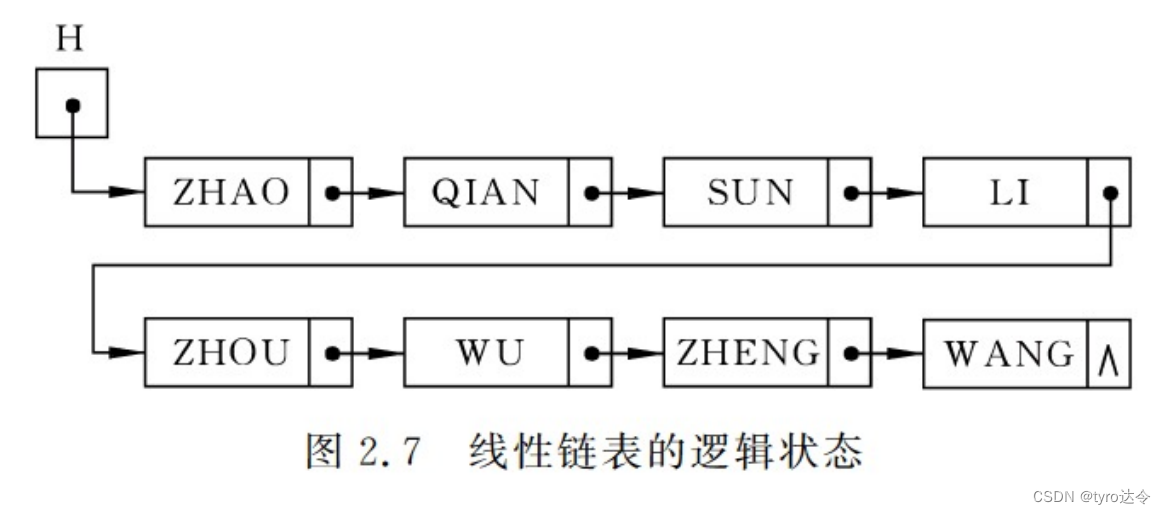
图2.7中H为 一“指针”变量,它的值为第一个结点的存储位置，第一个结点中的“指针”指向第二个结点，即它的值为第二个结点的存储位置,第二个结点中的“指针”指向第三个结点....,以此类推,直至最后一个结点。因为线性表的最后一个数据元素没有后继,因此最后一个结点中的“指针”是一个特殊的值“NULL"(在图上用^表示),通常称它为“空指针”。整个链表中的各个结点,即线性表的各个数据元素均可从指针H出发找到,称H为链表的“头指针”。在链表中,“结点”和“指针”是相互紧密关联的两个概念,需用C语言中的“结构指针”来描述。

下面先介绍有关“指针”的几个基本操作的含义.

若设 LNode *p,*q;

LinkList H;

则 p,q 和 H 均为以上定义的指针型变量。若 p 的值非空,则表明 p 指向某个结点,p->data表示 p 所指结点中的数据域,p->next 表示 p 所指结点中的指针域;若非空,则指向其“后继”结点。

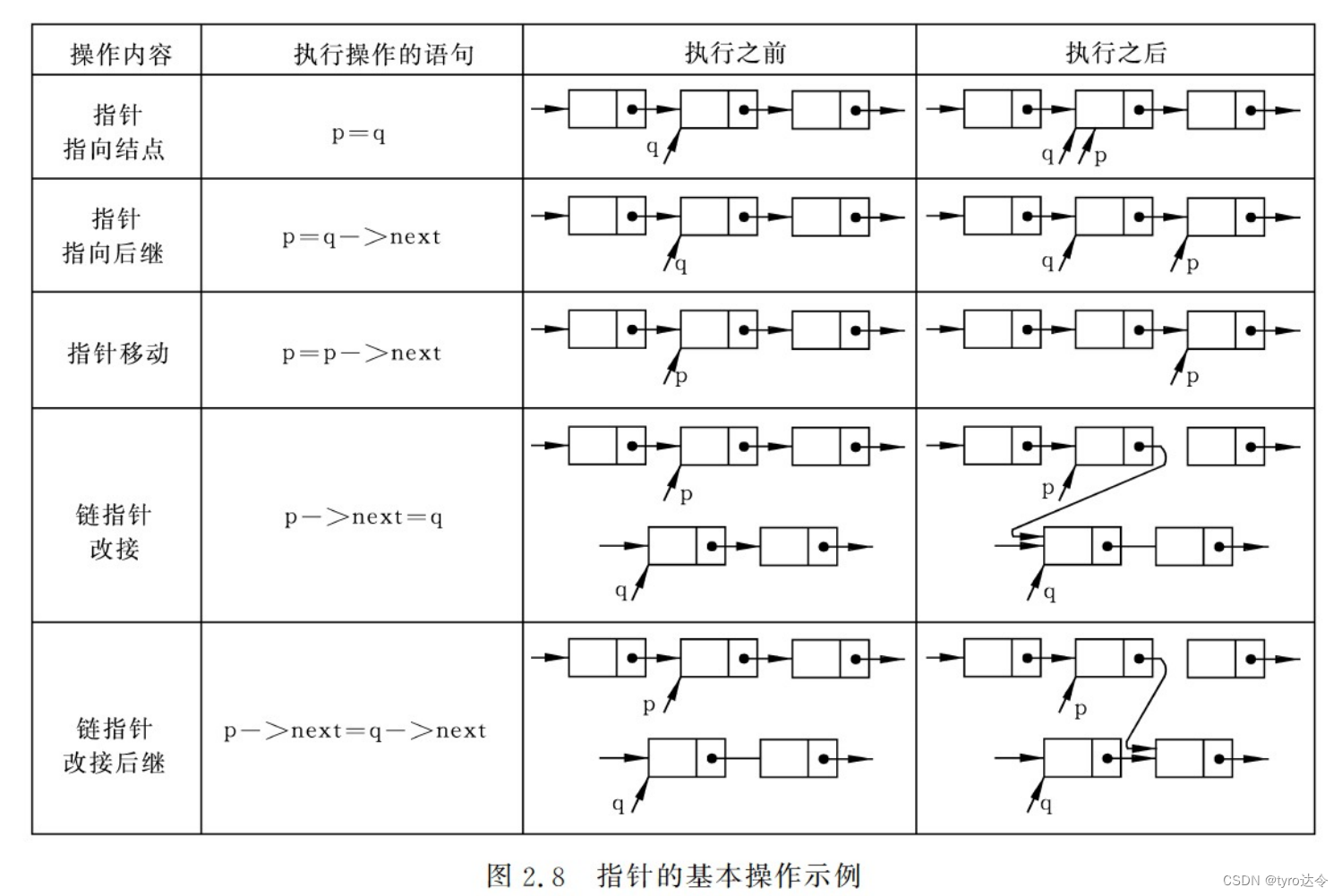
指针型变量只能作同类型的指针赋值与比较操作。并且,指针型变量的“值”除了由同类型的指针变量赋值得到外,都必须用 C 语言中的动态分配函数得到。例如,p=new LNode; 表示在运行时刻系统动态生成了一个 LNode 类型的结点,并令指针 p“指向”该结点。反之,当指针 p 所指结点不再使用,可用 delete p; 释放此结点空间。图 2.8 展示了若干种指针赋值语句以及这些语句执行前后指针值的变化状况。

二、单链表的基本操作

1.求线性表的长度

在顺序表中,线性表的长度是它的一个属性,因此很容易求得。但当以链表表示线性表时,整个链表由一个“头指针”来表示,线性表的长度即链表中的结点个数，只能通过“遍历’链表来得到。由此,需设一个指针 p 顺链向后扫描,同时设一个整型变量k随之进行“计数”。p 的初值为指向第一个结点,k 的初值为 0。若 p不空,则k增 1,令 p 指向其后继,如此循环直至 p 为“空”止,此时所得 k 值即为表长。

具体程序如下：

若 L 为空表,p 的初值为“NULL”,算法中 while 循环的执行次数为 0,则返回 k的值(即链表长度)为 0。显然，此算法的时间复杂度为 O(n),其中 n 为表长。

2.查找元素操作

在链表 L 中查找和给定值 e 相等的数据元素的过程和顺序表类似,从第一个结点起依次和 e 相比较,直至找到一个其值和 e 相等的元素,则返回它在链表中的“位置”;或者查遍整个链表都不存在这样的一个元素后,返回“NULL”。同样,在算法中,设置了一个指针变量 p 顺链扫描，直至 p 为“NULL”,或者 p->data 和 e 相同为止。

具体程序如下：

3.插入结点操作

由于在链表中不要求两个互为“前驱”和“后继”的数据元素紧挨存放，则在链表中插人一个新的数据元素时,不需要移动数据元素,而只需要在链表中添加一个新的结点,并修改相应的指针链接。

假设在链表中指针 p 所指结点之后插人一个指针 s 所指的结点,则只需分别修改指针p 和 s 所指结点的指针域的指针即可。用 C 语言描述为:

s->next=p->next; // s 结点的“后继”应是 p结点的“后继”

p->next= s; //插入之后，p结点的“后继”应为 s 结点

通常称这种插人为“后插”,后插操作前、后链表状态变化如图 2.9 所示。

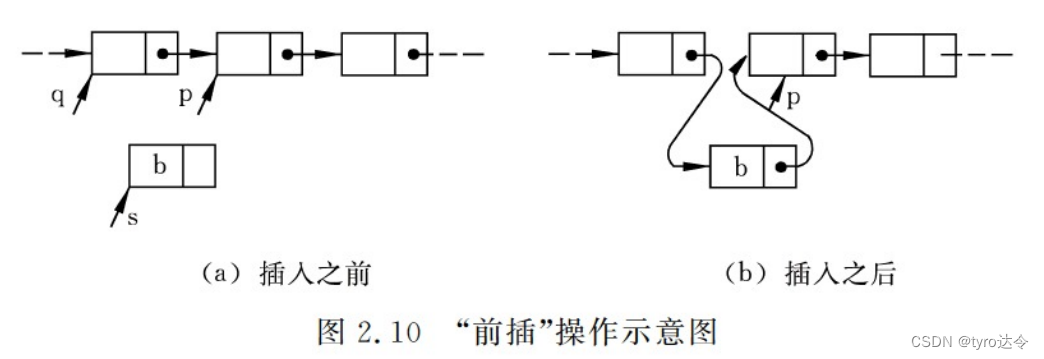
假设在链表中 p 结点之前插人一个 s 结点。此时,除了要修改 s 结点的指针域之外，还需要修改 p 的前驱结点的指针域,因为实现插入之后,p 结点不再是它“前驱”的“后继”，它“前驱”的“后继”应该是 s 结点。通常称这种插人为“前插”。一般情况下前插操作前、后链表状态变化如图 2.10 所示。假设指针 q 指向 p 结点的前驱结点,则描述“前插”修改指针的C语句为：

q-> next= s; // q结点的后继修改为 s 结点

s->next=p; //p结点修改为 s 结点的后继

可见,实现“前插”操作首先应该找到它的前驱结点,这只要从链表的头指针起进行查找即可。令 q 的初值等于头指针,查找结束的条件是 q->next==p;若否,则指针 q 后移。还有一点要注意的是,如果 p 所指结点是链表中的第一个结点,则“前插”操作尚需修改链表的头指针。

具体程序如下：

上述算法中,假定 p 确实指向链表中的某个结点,因此在查找其前驱结点时,不考虑查找不到的情况。

从以上两种插入操作的讨论可知,在链表中已知结点之后插入新的结点时,不需要进行查找。因此“后插”操作的时间复杂度为 O(1)。而在链表中已知结点之前进行插入时,虽然修改指针的时间是个常量,但由于需查找它的前驱，因此，“前插”操作的时间复杂度为O(n),其中n 为链表的长度。

4.删除结点操作

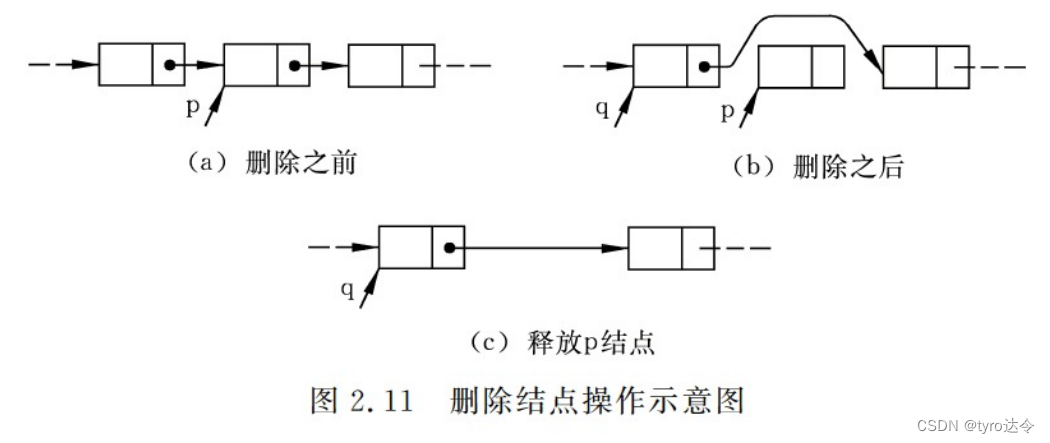
和插入类似,在链表中删除一个结点时,也不需要移动元素,仅需修改相应的指针链接。但由于删除结点时,需要修改的是它的“前驱”结点的指针域,因此和“前插”操作一样,首先应该找到它的前驱结点。如图 2.11 所示,假设待删除的是指针 p 所指结点,指针 q 指向它的前驱,则删除 p 结点将改变其前驱和后继的关系,q结点的后继不再是 p 结点,而应该是p 结点的后继,则应修改 q 结点的指针域,令它指向 p 结点的后继,即实现 q->next=p->next。同样,假如 p 结点是链表中的第一个结点,则尚需修改链表的头指针。

具体程序如下：

和前面讨论的前插类似,在上述算法中,假定 p 确实指向链表中的某个结点，因此在查找其前驱结点时,不考虑查找不到的情况。

容易看出,算法的时间复杂度亦为 O(n),其中 n 为链表的长度。