当前位置：首页 > news >正文

智能上线阻断的算法和实践

news 来源：原创 2024/11/15 10:22:18

一、背景

上线是引起系统故障的主要原因之一，在有些公司甚至能占到故障原因的一半，及时地发现并阻断、回滚存在故障隐患的上线，可以有效地减少系统故障。

事实上，现在很多平台已经提供了基于手工配置规则来进行变更阻断的能力。业务同学可以在平台上选取指标并设置相应的阈值，当上线中或上线后指标突破阈值范围时，则认为相关服务出现了异常，需要阻断。但是阈值需要人工确定，并且根据指标变化不断调整，所以往往难以覆盖大量的指标，限制了这种做法的有效性。

因此，我们希望能够通过算法自动检测指标的异常，从而可以覆盖大量的指标，提高变更阻断的覆盖度、便捷性和有效性。本文将系统地介绍我们在智能上线阻断中应用的算法和工程上的实践。

二、方案概述

一般来说，我们检测的是服务的黄金指标。黄金指标包括平响、可用性、QPM这三大类。当一个服务对外提供多个API时，每个API都会有这三个黄金指标。因此，一个服务的黄金指标就是所有这些API黄金指标的集合。

上线行为导致的服务异常可能有两种。第一种是变更的服务自身出现了异常，第二种是变更的服务自身没有出现异常，但与它有直接关联的其他服务出现了异常。因此在上线时，我们可以排查变更服务和与它有直接关联的其他服务的黄金指标。

因此，我们的方案是，首先让用户为每一个服务配置一个指标列表，在上线时由算法检查列表中的所有指标。如果发现异常，则可以阻断。每个服务的指标列表包括该服务自身的黄金指标，以及与该服务有关联的服务的黄金指标。

本文中我们将主要聚焦可用性，因为它是标识服务稳定性最核心的指标，往往能帮助我们快速、准确地发现故障。

三、算法原理

那么排查可用性指标的具体方法是什么？作为一个有常态化波动的指标，我们又怎样定义指标的“异常波动”呢？这些问题将在下文中详细解答。

一个API的可用性本质上是该API的成功率或者错误率，我们假设接口的总请求数为x, 错误数为y，传统的方法是为错误率（即y/x）设置一个经验的阈值，但当请求数较小的时候（例如夜间时刻），错误率的波动会很大，如下图所示：

上面三幅图分别为一个API的请求数，错误数和错误率，左侧红框标注的是一个真实的故障，但如果我们基于这个故障来设定错误率的阈值，则会发现在请求总数较低时，错误率很容易突破这个阈值，这也是直接手工配置规则来进行变更阻断的另一个问题。而二项分布可以较好地解决这一问题。

3.1 错误率指标检测的一般方法

首先，我们来介绍二项分布的数学原理，二项分布是大家所熟知的离散型概率分布了。它的数学定义如下：

在n次独立重复的伯努利试验（在同样的条件下重复地、相互独立地进行的一种随机试验，其特点是该随机试验只有两种可能结果）中，设每次试验中事件A发生的概率为p。用X表示n次试验中事件A发生的次数，随机变量X的离散概率分布即为二项分布。

对于错误率指标的监控来说，二项分布天然地比较适合，因为一个请求也像投硬币一样只有两种可能的状态：成功/失败。使用二项分布可以有效的解决以上问题。我们假设错误数y服从参数为x (请求总数)和p0 (基准错误率)的二项分布，则根据二项分布的定义有：

P \left\{y; x, p_0 \right\}=\binom{x}{y} p_0^y(1-p_0)^{x-y}P{y;x,p0}=(yx)p0y(1−p0)x−y

P \left\{y > y_j; x, p_0 \right\}=\sum_{k=y_j+1}^{xj}\binom{x_j}{k} p_0^k(1-p_0)^{x_j-k}P{y>yj;x,p0}=∑k=yj+1xj(kxj)p0k(1−p0)xj−k

为了简化计算，我们还可以假设yj服从正态分布，则根据二项分布的性质，该正态分布的均值为xj*p0, 方差为xj*p0*(1-p0),则yj在标准正态分布中的取值z为:

z=\frac{y_j-x_jp_0}{\sqrt{x_jp_0(1-p_0)}}=\frac{\frac{y_j}{x_j}-p_0}{\sqrt{p_0(1-p_0)}}\sqrt{x_j}z=xjp0(1−p0)yj−xjp0=p0(1−p0)xjyj−p0xj

根据以上第二个公式，在一次真实的上线中，我们可以选取上线后五分钟的总请求数为xj, 错误数为yj, 如果我们知道该接口的基准错误率p0的话，我们就可以据此计算出上线后一段时间内错误数高于当前观测值yj的概率，如果这一概率过小，我们就可以比较有信心的判定这次上线有异常了。简化计算后，可以将z与我们基于经验设定的阈值（例如8）来进行比较，从而直接判定是否异常。

3.2 如何确定基准错误率p0？

3.2.1确定基准错误率p0的三种方法

接下来的问题就是如何确定基准错误率p0了。我们总共会使用三种方法来分别确定一个p0.

第一，我们能够比较直观地想到使用上线前的数据来计算一个基准错误率，当基于这个错误率p0建立二项分布的模型，发现上线后一段时间的错误数高于观测值的概率过低时，则认为上线有异常.

第二，我们发现有些指标的错误率会有天级别的周期性波动，如下图1：

对于上图的情形，如果上线刚好在波谷处开始，并在波峰处结束，使用上线前20分钟的数据计算基准错误率会很容易将该次上线错误地判断为异常。所以，在实践中我们还会选取上线后昨日同时段的数据来计算第二个基准错误率p0, 按照与第一个p0同样的逻辑判断上线是否有异常.

第三，我们还发现，有些API的错误率虽然在上线前后有较大的变动，但即便错误率有所上升，其绝对值仍然较小（比如错误率从千分之一上涨为千分之二），在这种情况下我们认为应该放行上线，而不是阻断。因此，我们可以结合较长时间的历史数据来计算第三个基准错误率p0, 这一p0的计算涉及到KDE和LDA算法，比较复杂，将在后文中详细介绍。

进一步地，如果我们可以分别获取上线过程中已上线和尚未完成上线实例的请求总数和错误数，则可以根据尚未完成上线实例的数据计算基准错误率p0，从而计算出已完成上线实例错误数高于观测值的概率。这样，就可以实现上线过程中实时的上线阻断了。

综上，使用二项分布判断上线行为是否异常的示意图如下：

3.2.2使用KDE算法确定全局p0

当我们有一段较长时间的历史数据时，我们可以基于这些数据计算一个全局的基准错误率p0. 一个简单的想法是可以取整个数据集的平均值，但在实践中我们发现很多错误率指标有较多的突刺，如下图2所示：

如果对上图取平均值作为二项分布的基准错误率来进行检测，那当上线后的时间刚好在突刺处时，我们很可能会错误地阻断上线。所以我们很自然地想到可以取数据集的高分位值（比如99.9分位值）来作为基准错误率，但是当历史数据比较少的时候，取高分位值可能会直接取到数据集中的最大值或接近最大值的值，用这样的值作为基准错误率，效果也很差。

KDE算法就可以完美地解决这个问题，它的思想是，将数据集中的每个点视为一个分布，将这些分布累加起来，就可以得到整个原始数据集的分布。我们可以取这个分布的高分位值来作为全局阈值。比如，我们将每个点视为一个高斯分布，随着我们设定的高斯分布的标准差变大，整体分布的示意图如下：

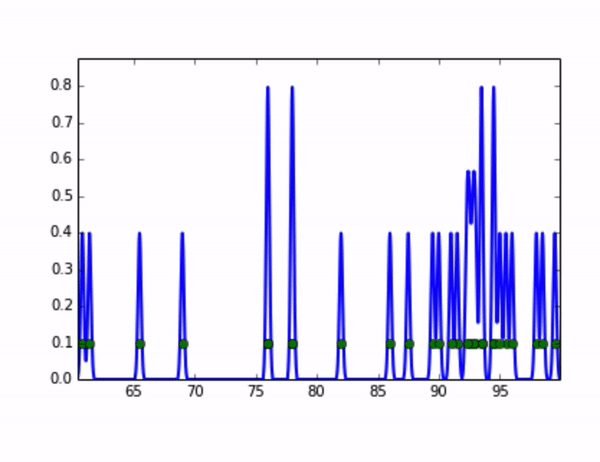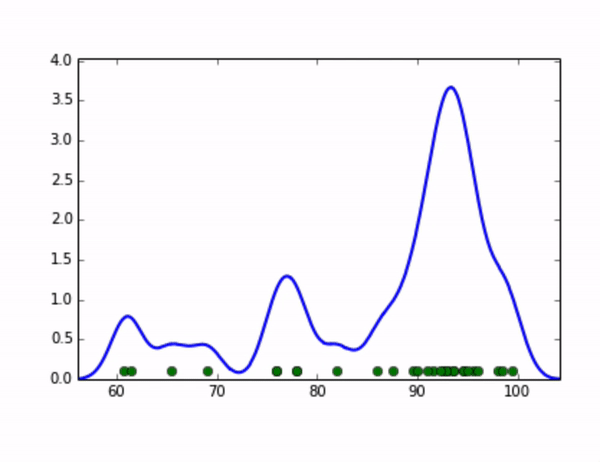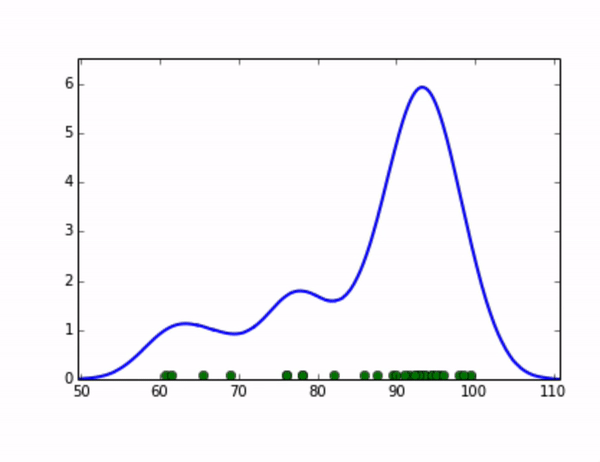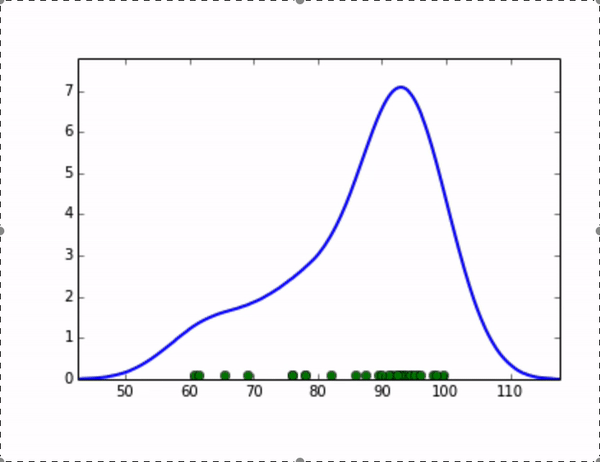
在统计学中，核密度估计（Kernel Density Estimation）算法是一种用来估计随机变量的概率密度函数(PDF: Probability Density Function)的非参数方法。我们可以用它来估算数据集的分布，在上面的例子中，对于每个点分布的假设对应了核密度估计算法中“核”的选取，而高斯分布的标准差则对应了步长（bandwidth）的选取，有一系列经典的算法可以求出步长的最优解，感兴趣的同学可以通过以下链接继续学习：https://jakevdp.github.io/blog/2013/12/01/kernel-density-estimation/

当我们通过KDE算法估计出了一个错误率的历史数据集的分布（即PDF）时，可以进一步地得到它的累计概率密度函数(CDF: Cumulative Distribution Function)和累计概率密度函数的反函数(ICDF: Inverse Cumulative Distribution Function)，而ICDF在0.999的取值，就是我们所希望求的全局阈值，即我们上文提到的第三个基准错误率p0。

那么，为什么ICDF在0.999的取值等同于数据集的99.9分位置，并且是一个合理的全局阈值呢？我们可以用下面两张示意图来简单的理解：

上面第一张图是一个数据集的概率密度函数曲线(PDF)，第二张图是该数据集的累计概率密度函数曲线(CDF)和累计概率密度函数的反函数曲线(ICDF)。我们知道CDF是PDF的积分，且PDF在整个定义域上的积分一定为1，而ICDF是CDF的反函数，所以ICDF的定义域为[0, 1]。现在，我们想为以上数据集取一个全局阈值，ICDF在0.999的取值就对应于CDF曲线在纵轴取值为0.999时横轴的取值，即PDF曲线下方面积为0.999时横轴的取值，示意图如下：

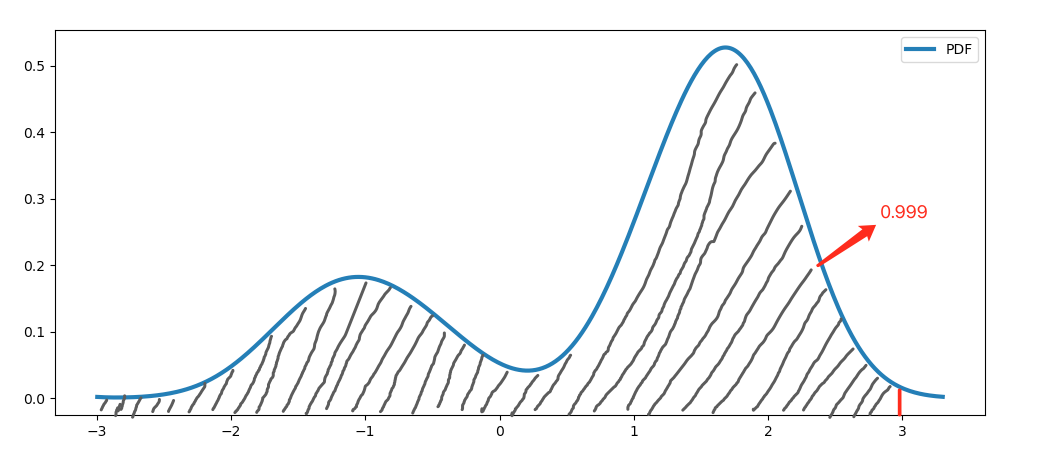
上图中红线对应的横轴取值，就是ICDF在0.999时的取值，直观的看，这确实是一个合理的全局阈值。

总体上，计算全局阈值的流程图如下：

3.2.3使用LDA算法去除异常点

在使用KDE算法计算全局阈值的时候会遇到一个问题：如果历史数据中本来就包含一部分的异常数据（如故障导致的错误率偏高），我们最后通过KDE算法取到的全局阈值会受到异常值的干扰，变得异常地高，这显然会使得我们检测的效果变差，如下图所示：

这时，就需要使用LDA算法来先对历史数据进行切分，切除历史数据中的异常值。

LDA (Linear Discriminant Analysis)译作线性判别分析，是一种统计学方法，主要用于分类和降维。其应用和一般形式比较复杂，感兴趣的同学可以自行以维基百科作为起点来学习：https://en.wikipedia.org/wiki/Linear_discriminant_analysis

在智能上线阻断服务中，我们会在计算全局阈值时用到LDA在一维形态下的简单形式，将错误率排序后的时间序列数据切为两段，从而将历史数据中可能存在的异常值切去。当然，如果我们发现LDA切走的数据太多，实际上意味着该数据集没有显著的异常值，可以不用切分，使用原始数据集即可。以上思想示意图如下：

LDA的数学原理如下：

假设我们有数据集：

x_1, x_2, x_3 ...... x_nx1,x2,x3......xn

将数据集排序：

x_1 \leq x_2 \leq x_3 ...... \leq x_nx1≤x2≤x3......≤xn

以为xi切分点，将数据集分为两个集合:

X_L: \left\{x_1, x_2...... x_i \right\}, X_R:\left\{x_{i+1}, x_{i+1}...... x_n \right\}XL:{x1,x2......xi},XR:{xi+1,xi+1......xn}

计算两个集合的均值：

\bar x_l, \bar x_rxˉl,xˉr

计算两个集合的方差之和：

s_w = \sum_{1}^{i} (x_k - \bar x_l)^2+ \sum_{i+1}^{n} (x_k - \bar x_r)^2sw=∑1i(xk−xˉl)2+∑i+1n(xk−xˉr)2

遍历i，求sw最小时i的取值即可。以sw为纵轴，i为横轴，在一个真实的数据集上遍历i的示意图如下：

上图中蓝色曲线的最小值就是我们要寻找的切分点，该点右侧的数据可以认为是异常值，需要切除。

切除异常值后再带入KDE算法计算，全局阈值会回到一个较为合理的范围，如下图所示：

3.3总结

本节介绍了如何通过二项分布、LDA、KDE算法来有效、智能地判断上线是否造成了服务的异常。实际上是通过二项分布将服务上线后的状态（或上线过程中已完成上线实例的状态）与我们认为的基准状态（上线前，上线后昨日同时段，全局阈值）进行比较，寻求指标波动的合理性解释，如果与三种基准状态比较都无法找到这种解释，则说明这次上线确实有异常。

四、工程实践

以上我们介绍了智能异常阻断的算法原理，本节将介绍智能上线阻断服务的工程实践，由于全局阈值计算需要的数据较多，计算量较大，需要离线训练，因此该服务的整体架构分为离线训练和在线检测两部分，如下图所示：

在服务开放前，业务同学需要配置服务与API的对应关系及API对应的可用性指标等。配置完成后，我们会离线训练前文提到的全局阈值并存在数据库中，当有上线发生时，SRE运维平台会调用我们的智能上线阻断平台，并传递服务名称，上线开始、结束的时间戳等参数，由智能上线阻断服务读取数据库中相关API指标数据和离线计算的全局阈值，并最终判断该上线行为是否异常，将结果返回给SRE运维平台，其中在线检测的详细流程图如下：