贪心算法专题
1.Acwing 1055. 股票买卖 II
题目链接:1055. 股票买卖 II - AcWing题库
思路:逢涨就买
#include<iostream>
using namespace std;
int main()
{
int n;
long long ans=0;
int a[100005];
cin>>n;
cin>>a[0];
for(int i=1;i<n;++i)
{
cin>>a[i];
if(a[i]>a[i-1]) ans+=a[i]-a[i-1];
}
cout<<ans<<endl;
return 0;
}2.ACwing 104. 货仓选址
题目链接:104. 货仓选址 - AcWing题库
思路:货仓一定在最中间的商店(即货仓左端的商店数一定等于货仓右边的商店数)
如果左右商店数不一样,如左边有2个,右边有4个
-------1--------2---------货仓-------3---------4---------5-----------6
那么,货仓往左移动d个单位,左边商店离货仓的总距离减少2d,右边商店离货仓的总距离增加4d,总距离增加2d。
同理可得,若货仓向右移动d个单位,总距离减少2d。
所以为了找到最佳选址,货仓现在应该向右移动,直到左右商店数都相等。
AC代码:
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
int n;
long long ans=0;
long long a[100005];
cin>>n;
for(int i=1;i<=n;++i)
{
cin>>a[i];
}
sort(a+1,a+n+1);
int mid=(n+1)>>1;
for(int i=1;i<=n;++i)
{
ans+=abs(a[i]-a[mid]);
}
cout<<ans<<endl;
return 0;
}3.Acwing 122. 糖果传递
题目链接:122. 糖果传递 - AcWing题库
思路:设最终每个小朋友最终得到M个糖果,第n个小朋友给第1个小朋友x1个糖果,第1个小朋友给第二个小朋友x2个糖果,以此类推,可以得到:
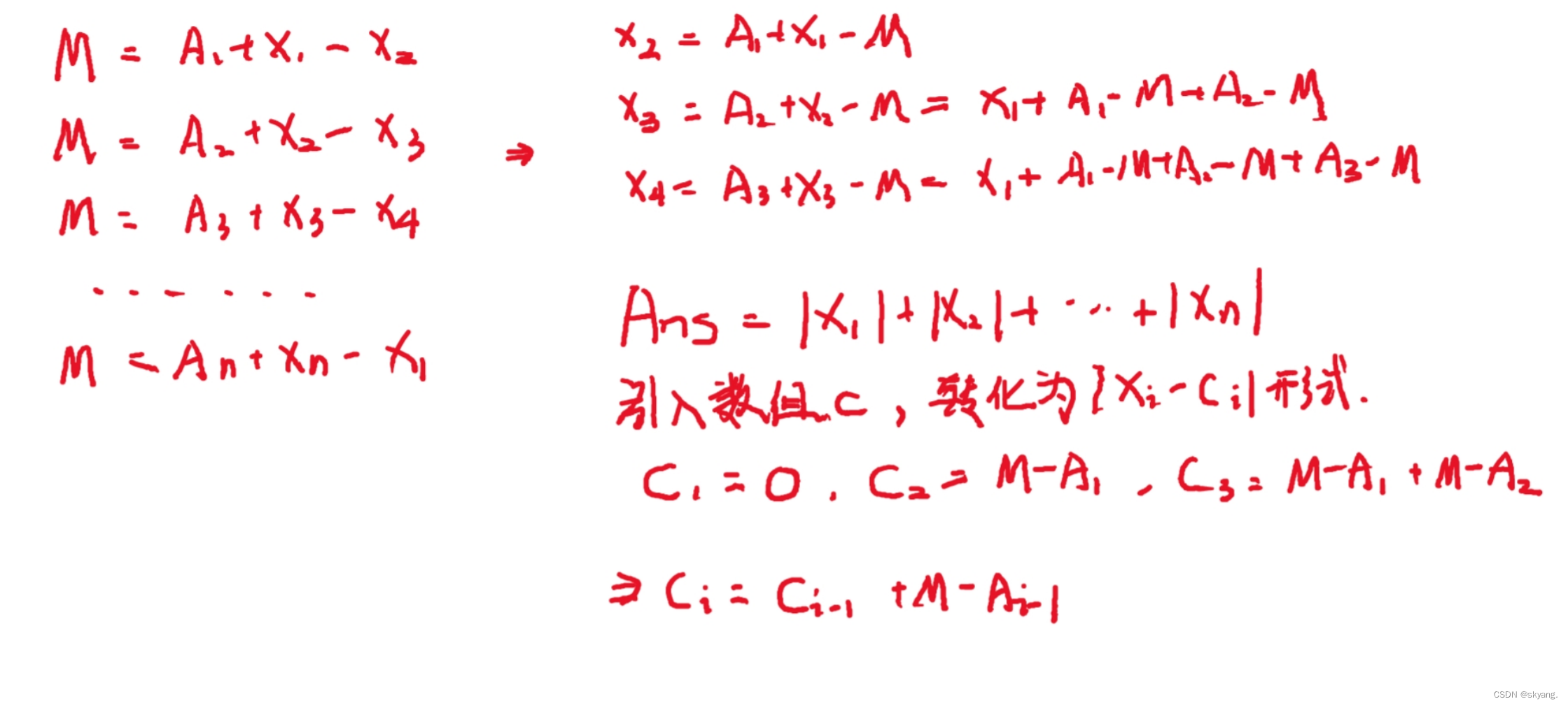
AC代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int MAXN = 1000005;
typedef long long ll;
int n;
int mid;
ll M=0,ans=0;
ll a[MAXN];
ll c[MAXN];
int main()
{
cin>>n;
for(int i=1;i<=n;++i)
{
scanf("%d",&a[i]);
M+=a[i];
}
M/=n;
mid=(n+1)>>1;
for(int i=2;i<=n;++i)
{
c[i]=c[i-1]+M-a[i-1];
}
sort(c+1,c+n+1);
for(int i=1;i<=n;++i)
{
ans+=abs(c[i]-c[mid]);
}
cout<<ans<<endl;
return 0;
}4. Acwing112. 雷达设备
题目链接:112. 雷达设备 - AcWing题库
思路:先算出每个小岛如果可以被覆盖的话,雷达可以设立的区间。
再根据每个区间的右端点 从小到大排序,每次选每段区间的右端点。
如果上次选择的右端点在这次的范围内,则这次的小岛已经被上次的雷达覆盖,不需再设雷达。
AC代码:
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int MAXN = 1005;
int x,y;
int n,d;
double len;
bool noAns;
double last = -1e20;
int ans=0;
struct Segment
{
double l,r;
bool operator<(const Segment a)const
{
return r<a.r;
}
}s[MAXN];
int main()
{
cin>>n>>d;
for(int i=0;i<n;++i)
{
cin>>x>>y;
if(y>d) noAns=true;
else
{
len=sqrt((double)d*d-y*y);
s[i]={x-len,x+len};
}
}
sort(s,s+n);
for(int i=0;i<n;++i)
{
if(last<s[i].l){
ans++;
last=s[i].r;
}
}
if(noAns) cout<<"-1"<<endl;
else cout<<ans<<endl;
return 0;
}5.Acwing 1235. 付账问题
题目链接:1235. 付账问题 - AcWing题库
评价:老6数据,最后一个测试点精度差0.0001
思路:先将每个人的钱数从小到大排序,如果这个人的钱低于平均值,那么他就得All in,同时后面的人也会因此付出更多的钱来弥补,当钱多的人弥补的钱数都相等时,方差最小。每次有人付不够钱,都要更新 每个人应付钱数的平均值,直到有人可以付清平均值的钱数(也意味着后面的所有人也都能付清钱),停止更新。
注意点:选用long double 提高精度
AC代码:
#include<iostream>
#include<algorithm>
#include<cmath>
#include<iomanip>
using namespace std;
const int MAXN = 500005;
int main()
{
int n;
int a[MAXN];
long double ans=0;
long double S;
long double tm,M;
cin>>n>>S;
for(int i=0;i<n;++i) cin>>a[i];
sort(a,a+n);
M=S/n;
tm=M;
for(int i=0;i<n;++i)
{
//tm=S/(n-i);
if(a[i]<tm)
{
ans+=(M-a[i])*(M-a[i]);
//S-=a[i];
tm+=(tm-a[i])/(n-i-1);
}
else
{
ans+=(M-tm)*(M-tm);
//S-=tm;
}
}
ans=sqrt(ans/n);
cout<<fixed<<setprecision(4)<<ans<<endl;
return 0;
}6.Acwing 1247. 后缀表达式
题目链接:1247. 后缀表达式 - AcWing题库
思路:分类讨论:
1.没有减号 那直接将所有数相加即可
2.有减号,且数据有正有负。可以利用减号将任意个负数变为正数
一个负数: -a a为负数
多个负数:-(a+b+c) a,b,c为负数
3.有减号,且数据都为正:将一个整数减两遍可以让他还是整数,但还必须减掉一个
例:a-(b-c-d)= a + c + d -b
4有减号,且数据都为负:打头的数字一定是加,必须加一个负数
AC代码:
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
const int MAXN = 200005;
int n,m;
ll a[MAXN];
ll ans=0;
int main()
{
cin>>n>>m;
for(int i=0;i<n+m+1;++i) cin>>a[i];
sort(a,a+n+m+1);
if(m==0)
{
for(int i=0;i<=n;++i) ans+=a[i];
}
else
{
if(a[0]>0)
{
ans=-a[0];
for(int i=1;i<n+m+1;++i) ans+=a[i];
}
else if(a[n+m]<0)
{
ans=a[n+m];
for(int i=0;i<n+m;i++) ans+=abs(a[i]);
}
else
{
for(int i=0;i<n+m+1;++i) ans+=abs(a[i]);
}
}
cout<<ans<<endl;
return 0;
}