当前位置：首页 > news >正文

Kruskal重构树学习笔记（C++）

news 来源：原创 2024/11/13 13:24:06

Kruskal重构树学习笔记

提示：

学习Kruskal重构树之前建议先了解一下Kruskal算法，虽然不了解这个影响不会很大

但一定要了解一下并查集的算法

接下来如果想要应用Kruskal重构树，一定要了解一下LCA算法

什么是Kruskal重构树

这里先简单说明一下Kruskal算法：

Kruskal算法依托于并查集算法实现

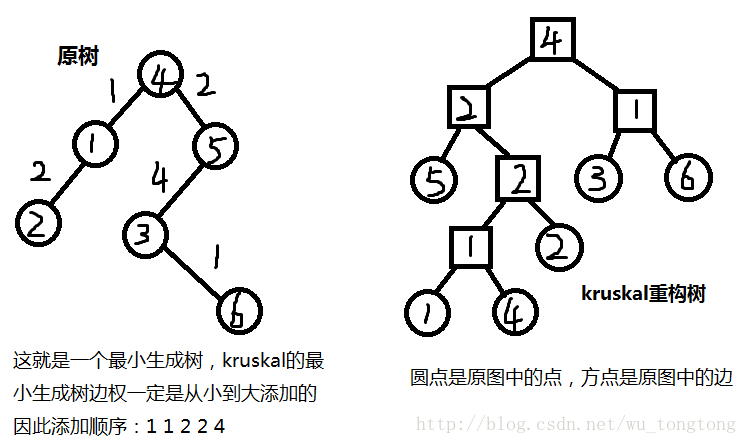
将一张图的边排序，从小到大依次将每一条边加入最小生成树，如果加入后会形成环，则不加入

Kruskal重构树的算法与其基本一致：

Kruskal重构树算法依托于并查集算法实现

（这里文字描述可能优点绕口，建议先看图再回来看文字）

将一张图的边排序，从小到大依次尝试每一条边

将边的两个节点的根节点（当一棵树只有一个节点时，它就是自己的根节点）连接到一个新创建节点上

赋予新创建节点权值，权值等于这条边的边权

循环，直至形成一棵树（所有点都在一个集合中）

这里写图片描述

*注：上图来自CSDN博主wu_tongtong：http://blog.csdn.net/wu_tongtong

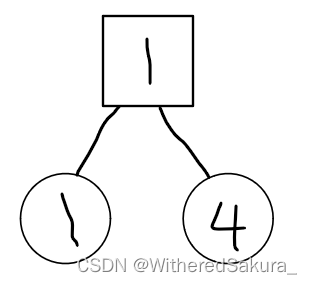
第一次合并，1和4间边权最小，合并1和4

在这里插入图片描述

第二次合并，3和6间边权最小，合并3和6

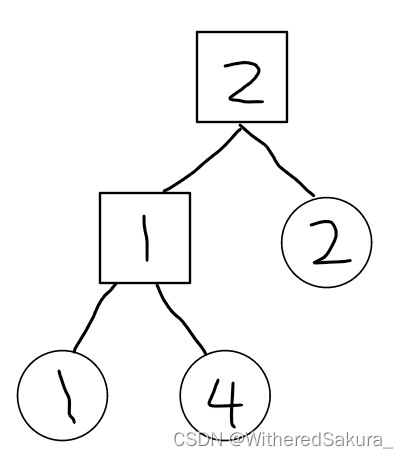
第三次合并，1和2间边权最小，合并2和1的根节点
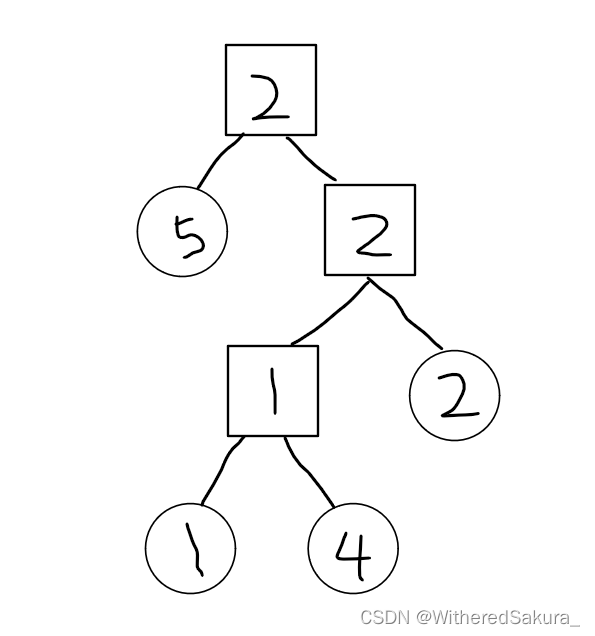
在这里插入图片描述

第四次合并，5和4间边权最小，合并5和2的根节点
在这里插入图片描述

Kruskal重构树的性质

1、二叉树

2、原树两点间路径上边权的最大值 = 新树两点间路径上点权的最大值

也就是说原树中两点之间路径上边权的最大值等于新树上两点的LCA的点权

3、子节点的点权小于等于父节点(大根堆)

Kruskal重构树的实现

讲解完了思路，接下来实现具体的代码

void exKruskal(int n) {
	edge t;
	int u, v;
	while (!p_q.empty()) {//p_q为优先队列（小根堆）
		t = p_q.top();
		p_q.pop();//取出最短边
		u = t.u; v = t.v;
		if (is_in_same(u, v)) continue;//会形成环
		//不会形成环
		n++;//从n + 1开始分配
		fa[n] = fa[u] = fa[v] = n;
		son[n][0] = u; son[n][1] = v;//连接
		value[n] = t.p;//赋值
	}
}