当前位置：首页 > news >正文

【代码随想录】96.不同的二叉搜索树

news 来源：原创 2024/11/16 3:41:20

96.不同的二叉搜索树

思路

请添加图片描述 n为1的时候有一棵树，n为2有两棵树，这个是很直观的。

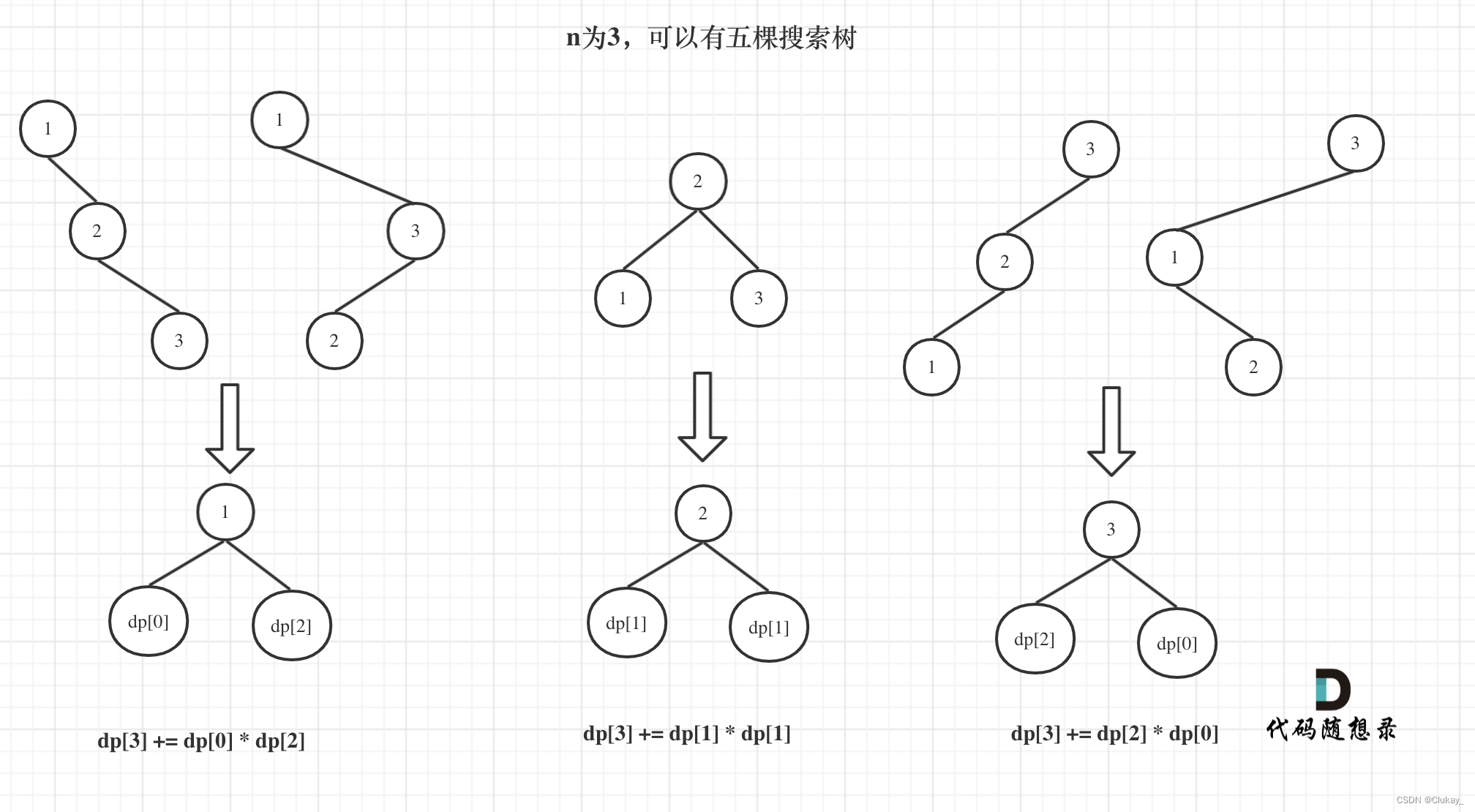
n为3的时候，有哪几种情况。

当1为头结点的时候，其右子树有两个节点，看这两个节点的布局，是不是和 n 为2的时候两棵树的布局是一样的啊！
当3为头结点的时候，其左子树有两个节点，看这两个节点的布局，是不是和n为2的时候两棵树的布局也是一样的啊！
当2为头结点的时候，其左右子树都只有一个节点，布局是不是和n为1的时候只有一棵树的布局也是一样的啊！

发现到这里，其实我们就找到了重叠子问题了，其实也就是发现可以通过dp[1] 和 dp[2] 来推导出来dp[3]的某种方式。

dp[3]，就是元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量

元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量

有2个元素的搜索树数量就是dp[2]。

有1个元素的搜索树数量就是dp[1]。

有0个元素的搜索树数量就是dp[0]。

所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
请添加图片描述

动态规划五部曲

1. 确定dp数组以及下标的含义
dp[i]： 1到i为节点组成的二叉搜索树的个数为dp[i]。
也可以理解是i个不同元素节点组成的二叉搜索树的个数为dp[i]

2. 确定递推公式
在上面的分析中，其实已经看出其递推关系，dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]

j相当于是头结点的元素，从1遍历到i为止。

所以递推公式：dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量

3. dp数组如何初始化
初始化，只需要初始化dp[0]就可以了，推导的基础，都是dp[0]。

那么dp[0]应该是多少呢？

从定义上来讲，空节点也是一棵二叉树，也是一棵二叉搜索树，这是可以说得通的。

从递归公式上来讲，dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0，也需要dp[以j为头结点左子树节点数量] = 1，否则乘法的结果就都变成0了。

所以初始化dp[0] = 1

4. 确定遍历顺序
首先一定是遍历节点数，从递归公式：dp[i] += dp[j - 1] * dp[i - j]可以看出，节点数为i的状态是依靠 i之前节点数的状态。

那么遍历i里面每一个数作为头结点的状态，用j来遍历。

代码如下：

for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= i; j++) {
        dp[i] += dp[j - 1] * dp[i - j];
    }
}

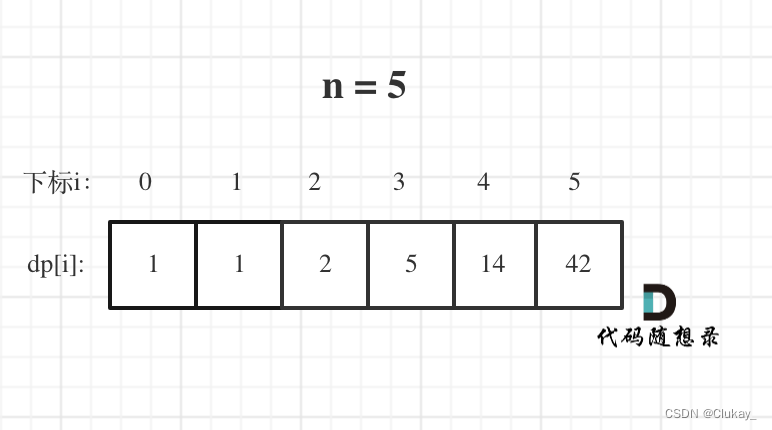
5. 举例推导dp数组
n为5时候的dp数组状态如图：
请添加图片描述

完整代码

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n + 1);
        dp[0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
};