【数据结构与算法】用队列实现栈用栈实现队列设计循环队列

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

• void push(int x) 将元素 x 压入栈顶。
• int pop() 移除并返回栈顶元素。
• int top() 返回栈顶元素。
• boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。
  
  

注意：

• 你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty
  这些操作。
• 你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 ,只要是标准的队列操作即可。
  
  

示例：

输入：
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2],[], [], []]
输出：
[null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回False

提示：

• 1 <= x <= 9
• 最多调用100 次 push、pop、top 和 empty
• 每次调用 pop 和 top 都保证栈不为空
  
  

进阶：你能否仅用一个队列来实现栈。

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

• void push(int x) 将元素 x 推到队列的末尾
• int pop() 从队列的开头移除并返回元素
• int peek()返回队列开头的元素
• boolean empty() 如果队列为空，返回 true ；否则，返回 false
  
  

说明：

你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例 1：

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2],[], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

提示：

• 1 <= x <= 9
• 最多调用 100 次 push、pop、peek 和 empty
• 假设所有操作都是有效的（例如，一个空的队列不会调用 pop 或者 peek 操作）

用两个栈实现队列的这道题和用两个队列实现栈的思路差不多。先在队列中定义两个栈，分别是入数据的栈pushST和出数据的栈popST。当入数据的时候，直接向栈pushST入数据。当出数据时，需要考虑两种情况：如果栈popST中没有数据，就将pushST中的数据导过去，再将栈pushST栈顶的数据 pop 掉；如果popST中有数据，直接 pop 掉栈顶的数据就行了。

typedef int STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;
	int capacity;
}ST;

void StackInit(ST* ps);
void StackDestroy(ST* ps);
void StackPush(ST* ps, STDataType x);
void StackPop(ST* ps);

STDataType StackTop(ST* ps);
bool StackEmpty(ST* ps);
int StackSize(ST* ps);

void StackInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}

void StackDestroy(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}

void StackPush(ST* ps, STDataType x)
{
	assert(ps);
	if (ps->capacity == ps->top)
	{
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->a, newcapacity * sizeof(STDataType));
		if (tmp == NULL)
		{
			perror("relloc fail");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity = newcapacity;
	}
	ps->a[ps->top] = x;
	ps->top++;
}

void StackPop(ST* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	ps->top--;
}

STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->a[ps->top - 1];
}

bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}

int StackSize(ST* ps)
{
	assert(ps);
	return ps->top;
}

//匿名结构体
typedef struct 
{
    ST pushST;
    ST popST;
} MyQueue;


MyQueue* myQueueCreate() 
{
    MyQueue* q = (MyQueue*)malloc(sizeof(MyQueue));
    StackInit(&q->pushST);
    StackInit(&q->popST);
    return q;
}

void myQueuePush(MyQueue* obj, int x) 
{
    StackPush(&obj->pushST, x);
}

int myQueuePop(MyQueue* obj) 
{
    //如果popST中没有数据，将pushST中的数据导过去
    //popST中的数据就符号先进先出的顺序了
    //如果popST中有数据，那么就直接pop popST中的数据
    if(StackEmpty(&obj->popST))
    {
        while(!StackEmpty(&obj->pushST))
        {
            StackPush(&obj->popST, StackTop(&obj->pushST));
            StackPop(&obj->pushST);
        }
    }

    int front = StackTop(&obj->popST);
    StackPop(&obj->popST);
    return front;
}

int myQueuePeek(MyQueue* obj) 
{
    if(StackEmpty(&obj->popST))
    {
        while(!StackEmpty(&obj->pushST))
        {
            int top = StackTop(&obj->pushST);
            StackPop(&obj->pushST);
            StackPush(&obj->popST, top);
        }
    }
    return StackTop(&obj->popST);
}

bool myQueueEmpty(MyQueue* obj) 
{
    return StackEmpty(&obj->pushST) && StackEmpty(&obj->popST);
}

void myQueueFree(MyQueue* obj) 
{
    StackDestroy(&obj->pushST);
    StackDestroy(&obj->popST);
    free(obj);
}

设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：

• MyCircularQueue(k): 构造器，设置队列长度为 k。
• Front: 从队首获取元素。如果队列为空，返回 -1 。
• Rear: 获取队尾元素。如果队列为空，返回 -1 。
• enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
• deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
• isEmpty(): 检查循环队列是否为空。
• isFull():检查循环队列是否已满。
  
  

示例：

MyCircularQueue circularQueue = newMyCircularQueue(3); // 设置长度为 3
circularQueue.enQueue(1); // 返回 true circularQueue.enQueue(2); // 返回true circularQueue.enQueue(3); // 返回 true circularQueue.enQueue(4); // 返回 false，队列已满
circularQueue.Rear(); // 返回 3
circularQueue.isFull(); // 返回 true circularQueue.deQueue(); // 返回true circularQueue.enQueue(4); // 返回 true circularQueue.Rear(); //返回 4

提示：

• 所有的值都在 0 至 1000 的范围内；
• 操作数将在 1 至 1000 的范围内；
• 请不要使用内置的队列库。

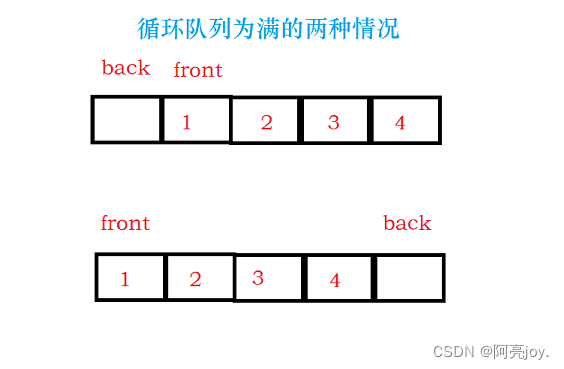
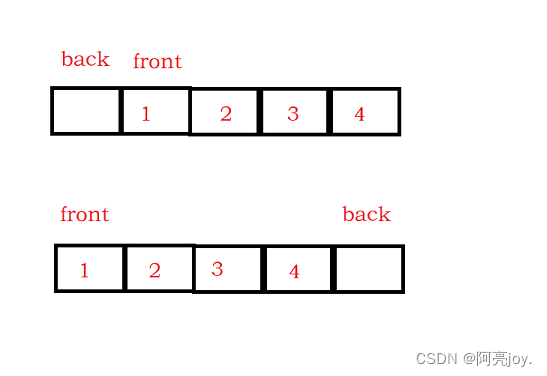
本道题需要实现的函数接口有：创建循环链表、判断循环链表是否为空、判断循环链表是否为满、数据入队、数据出队、返回队头数据、返回队尾数据以及销毁循环队列。循环队列可以采用数组或者链表的形式实现，但不管使用数组还是链表来实现循环队列，需要多开一个空间或者加个size记录循环队列中数据的个数，否则无法将队列为空和队列为满两种情况区分开。

//重点：循环队列，无论使用数组实现还是链表实现，都要
//多开一个空间，也就意味着，要是一个存k个数据的循环队列
//要开k+1个空间，否则无法实现判空和判满。

//数组实现：空：front == tail  满：(tail+1)%(k+1) == front
//链表实现：空：tail == tail 满：tail->next == front

typedef struct 
{
    int* a;
    int front;
    int back;
    int N;
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) 
{
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a = (int*)malloc(sizeof(int)*(k+1));
    obj->front = obj->back = 0;
    obj->N = k + 1;

    return obj;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) 
{
    return obj->front == obj->back;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) 
{
    return (obj->back + 1) % obj->N == obj->front;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) 
{
    if(myCircularQueueIsFull(obj))
        return false;
    
    obj->a[obj->back] = value;
    obj->back++;
    // 当back在最后一个位置时，让back回到下标为0的位置
    obj->back %= obj->N;
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
        return false;
    
    obj->front++;
    // 当front在最后一个位置时，让front回到下标为0的位置
    obj->front %= obj->N;

    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
        return -1;
    else
        return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) 
{
    // if(myCircularQueueIsEmpty(obj))
    //     return -1;
    // else if(obj->back == 0)
    //     return obj->a[obj->N -1];
    // else    
    //     return obj->a[obj->back - 1];

    if(myCircularQueueIsEmpty(obj))
        return -1;
    else
        return obj->a[(obj->back - 1 + obj->N) % obj->N];
}

void myCircularQueueFree(MyCircularQueue* obj) 
{
    free(obj->a);
    free(obj);
}

自定义循环队列

a：整型指针，指向申请的空间
front：队头的位置
back：队尾位置的下一个位置
N：数组的长度 = k + 1

typedef struct 
{
    int* a;
    int front;
    int back;
    int N;
} MyCircularQueue;

创建循环链表

需要注意的是，要给队列循环申请 k + 1个空间，来区分队列是空还是满

MyCircularQueue* myCircularQueueCreate(int k) 
{
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a = (int*)malloc(sizeof(int)*(k+1));
    obj->front = obj->back = 0;
    obj->N = k + 1;

    return obj;
}

判断循环队列是否为空

当obj->front == obj->back时，循环队列为空

bool myCircularQueueIsEmpty(MyCircularQueue* obj) 
{
    return obj->front == obj->back;
}

判断循环队列是否为满

当(obj->back + 1) % obj->N == obj->front时，循环队列为满

bool myCircularQueueIsFull(MyCircularQueue* obj) 
{
    return (obj->back + 1) % obj->N == obj->front;
}

数据入队

1.当循环队列为满时，返回 false
2.当循环队列不为满时，数据入队obj->a[obj->back] = value, obj->back++
3.当back在最后一个位置时，让back回到下标为 0 的位置obj->back %= obj->N

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) 
{
    if(myCircularQueueIsFull(obj))
        return false;
    
    obj->a[obj->back] = value;
    obj->back++;
    // 当back在最后一个位置时，让back回到下标为0的位置
    obj->back %= obj->N;
    return true;
}

数据出队

1.当循环队列为空时，返回 false
2.当循环队列不为空时，数据出队obj->front++
3.当front在最后一个位置时，让front回到下标为 0的位置obj->front %= obj->N

bool myCircularQueueDeQueue(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
        return false;
    
    obj->front++;
    // 当front在最后一个位置时，让front回到下标为0的位置
    obj->front %= obj->N;

    return true;
}

返回队头数据

1.当循环队列为空时，返回 false
2.当循环队列不为空时，返回队头数据return obj->a[obj->front]

int myCircularQueueFront(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
        return -1;
    else
        return obj->a[obj->front];
}

返回队尾数据

1.当循环队列为空时，返回 false
2.当循环队列不为空时，返回队尾数据return obj->a[(obj->back - 1 + obj->N) % obj->N]

int myCircularQueueRear(MyCircularQueue* obj) 
{
    // if(myCircularQueueIsEmpty(obj))
    //     return -1;
    // else if(obj->back == 0)
    //     return obj->a[obj->N -1];
    // else    
    //     return obj->a[obj->back - 1];

    if(myCircularQueueIsEmpty(obj))
        return -1;
    else
        return obj->a[(obj->back - 1 + obj->N) % obj->N];
}

销毁循环队列

void myCircularQueueFree(MyCircularQueue* obj) 
{
    free(obj->a);
    free(obj);
}