当前位置：首页 > news >正文

[算法入门笔记] 19. 有序表

news 来源：原创 2024/12/21 4:52:42

有序表部分，有时间详细优化

文章目录

- Binary Search Tree
- - 结点结构
  - 创建结点
  - 查找结点
  - 插入结点
  - 删除结点
  - 结点是否存在
  - 找最小值
  - 找最大值
  - 找后继
  - 找前驱
- Self Balancing Binary Tree
- - 左旋转
  - 右旋转
- AVL Tree
- - 结点结构
  - 创建结点
  - 插入结点
  - 删除结点
  - 平衡调整
- Size Balanced Tree
- - HashMap
- 红黑树
- 跳表

Binary Search Tree

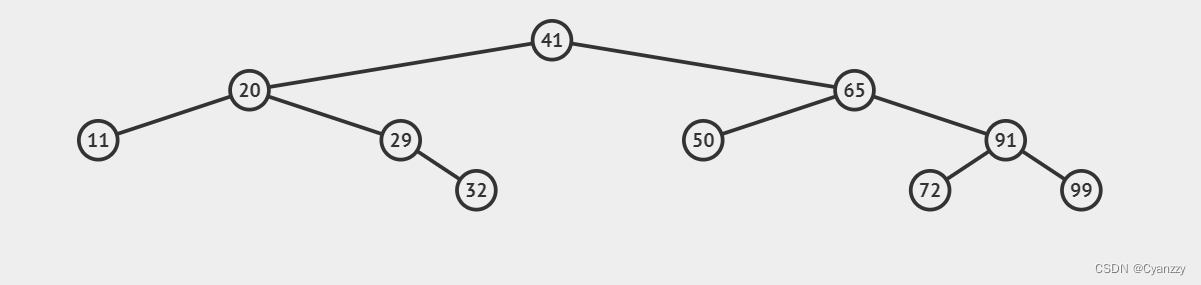
在这里插入图片描述

性质

对于树中的每个节点x，它的左子树中所有关键字值小于x的关键字值，它的右子树关键字值大于x的关键字值

结点结构

public static class Node {
    /**
     * 构造函数
     * @param value 结点的值
     * @param parent 结点的父亲结点
     * @param left 结点的左孩子结点
     * @param right 结点的右孩子结点
     */
    public Node(Integer value, Node parent, Node left, Node right) {
        super();
        this.value = value;
        this.parent = parent;
        this.left = left;
        this.right = right;
    }

    public Integer value;
    public Node parent;
    public Node left;
    public Node right;

    /**
     * 叶子节点判断
     * @return
     */
    public boolean isLeaf() {
        return left == null && right == null;
    }

    @Override
    public int hashCode() {
        final int prime = 31;
        int result = 1;
        result = prime * result + ((value == null) ? 0 : value.hashCode());
        return result;
    }

    @Override
    public boolean equals(Object obj) {
        if (this == obj)
            return true;
        if (obj == null)
            return false;
        if (getClass() != obj.getClass())
            return false;
        Node other = (Node) obj;
        if (value == null) {
            if (other.value != null)
                return false;
        } else if (!value.equals(other.value))
            return false;
        return true;
    }
}

创建结点

/**
 * 创建结点
 * @param value
 *            结点的值
 * @param parent
 *            结点的父亲结点
 * @param left
 *            结点的左孩子结点
 * @param right
 *            结点的右孩子结点
 * @return 创建一个结点的实例
 */
protected Node createNode(int value, Node parent, Node left, Node right) {
    return new Node(value, parent, left, right);
}

查找结点

/**
 * 根据结点的值查找结点，如果它不存在返回null
 *
 * @param element
 *            结点值
 * @return 根据提供的值查找结点，如果结点不存在，返回null
 */
public Node search(int element) {
    Node node = root;
    while (node != null && node.value != null && node.value != element) {
        // 如果值小于Node结点，则查找Node结点的左孩子
        if (element < node.value) {
            node = node.left;
        } else {
            // 如果值大于Node结点，则查找Node结点的右孩子
            node = node.right;
        }
    }
    return node;
}

插入结点

/**
 * 插入新的结点
 *
 * @param element
 *            待插入的元素
 */
public Node insert(int element) {
    // 如果树为空，实例化新结点
    if (root == null) {
        root = createNode(element, null, null, null);
        size++;
        return root;
    }

    // 待插入结点的父亲结点
    Node insertParentNode = null;
    // 哨兵结点
    Node searchTempNode = root;
    while (searchTempNode != null && searchTempNode.value != null) {
        // 父亲结点指向哨兵结点
        insertParentNode = searchTempNode;
        if (element < searchTempNode.value) { // 如果值小于searchTempNode的值，查找searchTempNode的左孩子
            searchTempNode = searchTempNode.left;
        } else { // 如果值大于searchTempNode的值，查找searchTempNode的右孩子
            searchTempNode = searchTempNode.right;
        }
    }

    // newNode存储待插入结点的信息
    Node newNode = createNode(element, insertParentNode, null, null);
    // newNode信息和父亲结点信息比较，选择插入的位置
    if (insertParentNode.value > newNode.value) { // 如果newNode值小于父亲结点的值，newNode就作为父亲结点左孩子
        insertParentNode.left = newNode; 
    } else {
        insertParentNode.right = newNode; // 如果newNode值大于父亲结点的值，newNode就作为父亲结点的右孩子
    }

    // 更新树的大小
    size++;
    // 返回新结点
    return newNode;
}

删除结点

假设二叉搜索树上被删除的结点为p，f为其双亲结点，则删除结点p分三种情况：

1.p结点为叶子结点，直接删除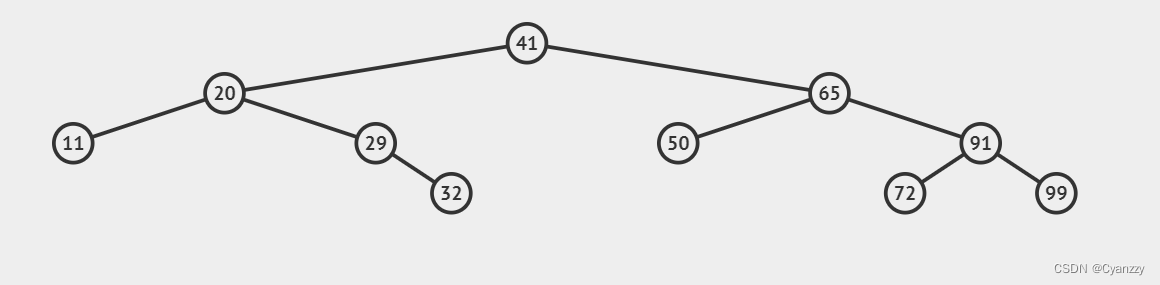

例如，删除72结点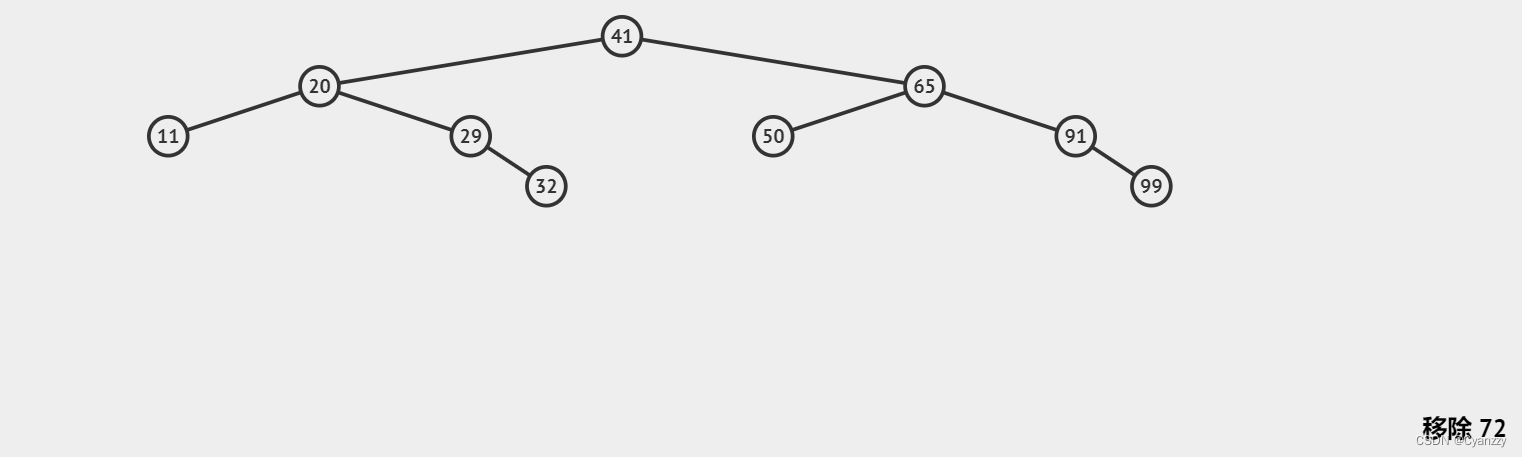
2.p结点只有右子树，而无左子树，或者只有左子树，而无右子树。此时只需要将p删掉，然后将p的子树直接连在原来p与其双亲结点f相连的指针上即可
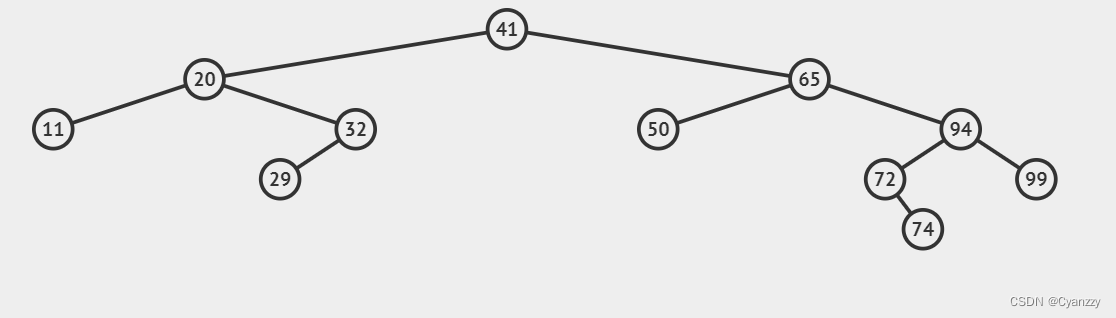
3.p结点既有左子树又有右子树。此时，先沿p的左子树根结点的右指针一直往右走，直到来到其右子树的最右边的一个结点r
- （也可以沿着p右子树根结点的左指针一直往左走，直到来到其左子树的最左边的一个结点）。
- 然后将p中的关键字用r中的关键字代替
- 最后判断，如果r是叶子结点，用情况1的方法删除；如果不是叶子结点，用情况2的方法删除
例如，删除91结点

/**
 * 如果结点值存在，删除结点
 *
 * @param element
 *            待移除结点的值
 *
 * @return 新结点取代被移除的结点，如果值未在二叉搜索树中找到，返回空
 */
public Node delete(int element) {
    // 返回待移除元素的位置
    Node deleteNode = search(element);
    if (deleteNode != null) {
        return delete(deleteNode);
    } else {
        return null;
    }
}

/**
 * 当待删除结点存在时删除结点
 *
 * @param deleteNode
 *           待删除的结点
 *
 * @return 新结点取代被移除的结点，如果值未在二叉搜索树中找到，返回空
 */
protected Node delete(Node deleteNode) {
    if (deleteNode != null) {
        Node nodeToReturn = null;
        if (deleteNode != null) {
            if (deleteNode.left == null) { // 1.deleteNode可能有右子树可能没有右子树，一定没有左子树
                // 待删除结点的左孩子为空，用其右孩子代替待删除结点
                nodeToReturn = transplant(deleteNode, deleteNode.right);
            } else if (deleteNode.right == null) { // 2.deleteNode只有左子树
                // 待删除结点的右孩子为空，用其左孩子代替待删除结点
                nodeToReturn = transplant(deleteNode, deleteNode.left);
            } else { // 3.deleteNode有两个子树
                // successorNode存储待删除结点右孩子的最左边的结点
                Node successorNode = getMinimum(deleteNode.right);
                // 如果successorNode的父指针不是待删除结点，
                // 如果deleteNode是successorNode的直接父亲，successorNode右孩子不用处理，successorNode直接取代待删除结点
                if (successorNode.parent != deleteNode) {
                    // 用successorNode的右孩子取代successorNode
                    transplant(successorNode, successorNode.right);
                    // successorNode的右孩子指向待删除结点的右孩子
                    successorNode.right = deleteNode.right;
                    // successorNode右孩子的父指针指向successorNode
                    successorNode.right.parent = successorNode;
                }
                // successorNode取代待删除结点
                transplant(deleteNode, successorNode);
                // successorNode的左孩子指向待删除结点的左孩子
                successorNode.left = deleteNode.left;
                // successorNode的左孩子的父指针指向successorNode
                successorNode.left.parent = successorNode;
                // 返回successorNode
                nodeToReturn = successorNode;
            }
            // 更新树的大小
            size--;
        }
        return nodeToReturn;
    }
    // 如果没找到直接返回null
    return null;
}

/**
 * 用newNode取代nodeToReplace的位置
 *
 * @param nodeToReplace
 *            将被newNode代替的结点，并且将nodeToReplace移除
 * @param newNode
 *           新结点
 *
 * @return 返回新代替的结点
 */
private Node transplant(Node nodeToReplace, Node newNode) {
    if (nodeToReplace.parent == null) { // nodeToReplace所在树中只有一个结点
        this.root = newNode;
    } else if (nodeToReplace == nodeToReplace.parent.left) { // nodeToReplace是其父亲的左孩子，将其父亲左孩子更新成newNode
        nodeToReplace.parent.left = newNode;
    } else { // nodeToReplace是其父亲的右孩子，将其父亲右孩子更新成newNode
        nodeToReplace.parent.right = newNode;
    }
    // 更新newNode的父指针
    if (newNode != null) {
        newNode.parent = nodeToReplace.parent;
    }
    // 返回newNode
    return newNode;
}

结点是否存在

/**
 * 判断element是否存在树中
 * @param element
 * @return 如果树中包含该值，返回true
 */
public boolean contains(int element) {
    return search(element) != null;
}

找最小值

/**
 * 找到二叉搜索树的最左边的结点
 * @return 返回最小值
 */
public int getMinimum() {
    return getMinimum(root).value;
}

protected Node getMinimum(Node node) {
    while (node.left != null) {
        node = node.left;
    }
    return node;
}

找最大值

/**
 * 返回二叉搜索树的最右边的结点
 * @return Maximum element in tree.
 */
public int getMaximum() {
    return getMaximum(root).value;
}

protected Node getMaximum(Node node) {
    while (node.right != null) {
        node = node.right;
    }
    return node;
}

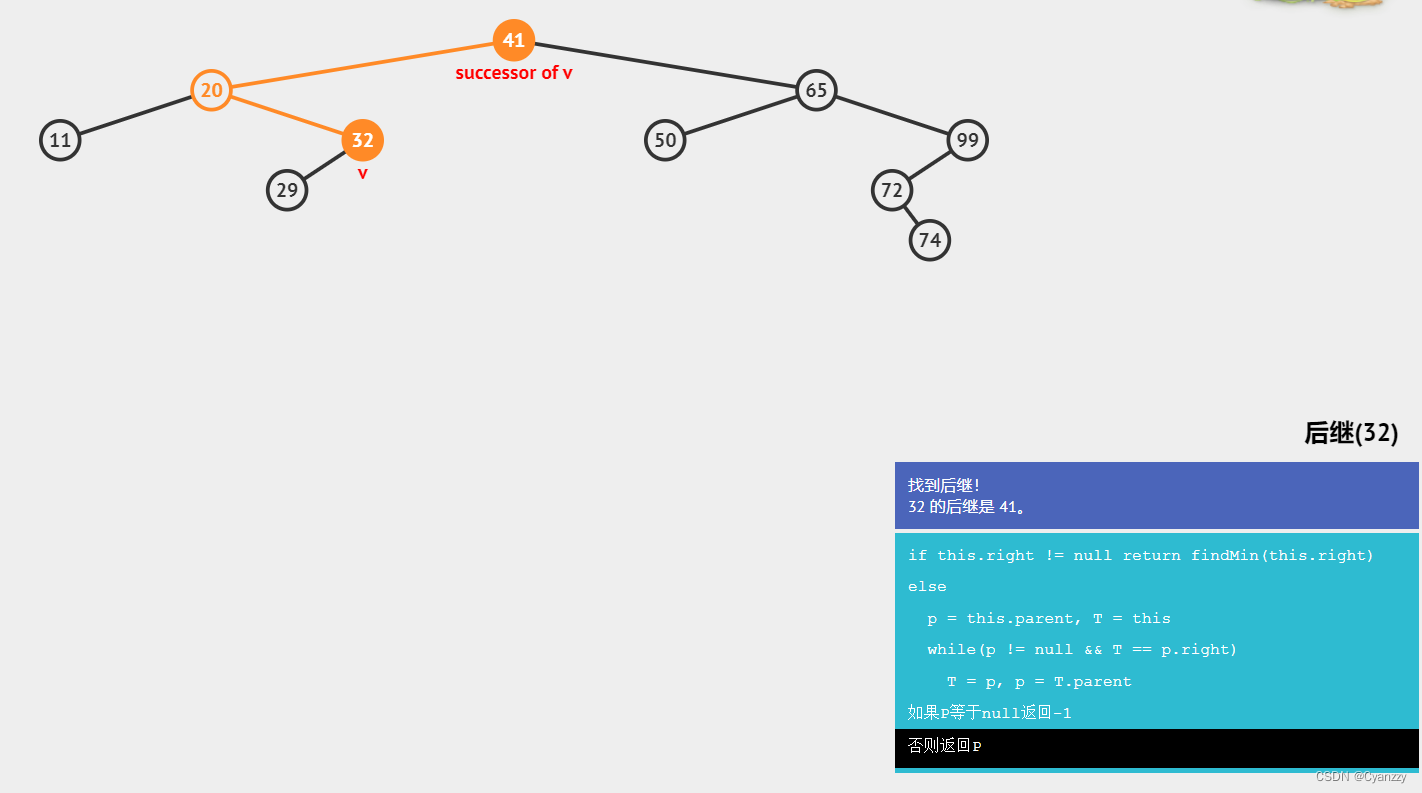
找后继

/**
 * 返回元素后继
 *
 * @param element 待查找元素
 *            
 * @return 该元素的后继
 */
public int getSuccessor(int element) {
    return getSuccessor(search(element)).value;
}

protected Node getSuccessor(Node node) {
    // 如果结点有右孩子，它的后继是该结点右孩子的最左边的值
    if (node.right != null) {
        return getMinimum(node.right);
    } else { 
        // 当前结点指向Node
        Node currentNode = node;
        // Node父亲指针
        Node parentNode = node.parent;
        while (parentNode != null && currentNode == parentNode.right) {
            //currentNode指向父亲结点
            currentNode = parentNode;
            // 父亲结点往上回溯
            parentNode = parentNode.parent;
        }
        return parentNode;
    }
}

在这里插入图片描述

找前驱

在这里插入图片描述

/**
 * 返回元素前驱
 * @param element 待查找元素
 * @return 该元素的前驱
 */
public int getPredecessor(int element) {
    return getPredecessor(search(element)).value;
}

protected Node getPredecessor(Node node) {
    // 如果结点有左孩子，它的前驱是该节点的左孩子的最右边的值
    if (node.left != null) {
        return getMaximum(node.left);
    } else {
        // 当前结点指向Node
        Node currentNode = node;
        // Node父亲指针
        Node parentNode = node.parent;
        while (parentNode != null && currentNode == parentNode.left) {
            currentNode = parentNode;
            parentNode = parentNode.parent;
        }
        return parentNode;
    }
}

Self Balancing Binary Tree

由于要保证二叉搜索树的性质，当前结点左旋转表示当前结点要挂在左边，所以其右孩子要上去才能保证二叉搜索树的性质，因此用待旋转结点的右孩子代替它
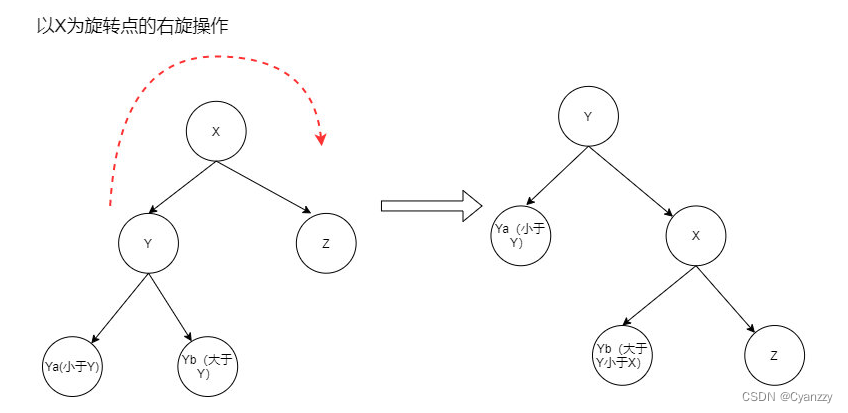
由于要保证二叉搜索树的性质，当前结点右旋转表示当前结点要挂在右边，所以其左孩子要上去才能保证二叉搜索树的性质，因此用待旋转结点的左孩子代替它

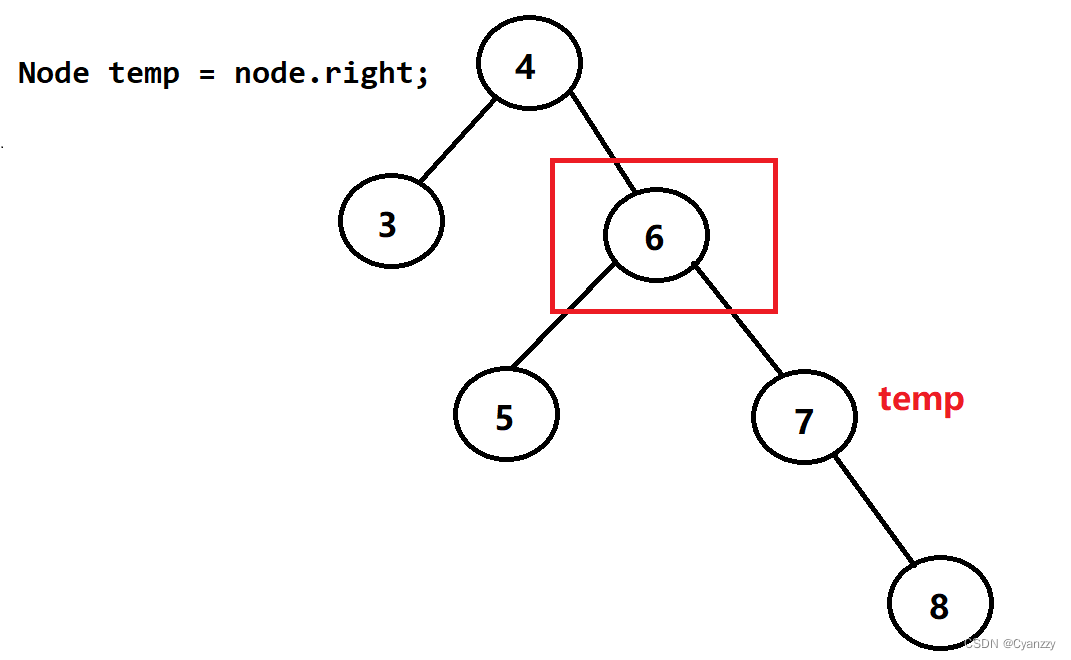
左旋转

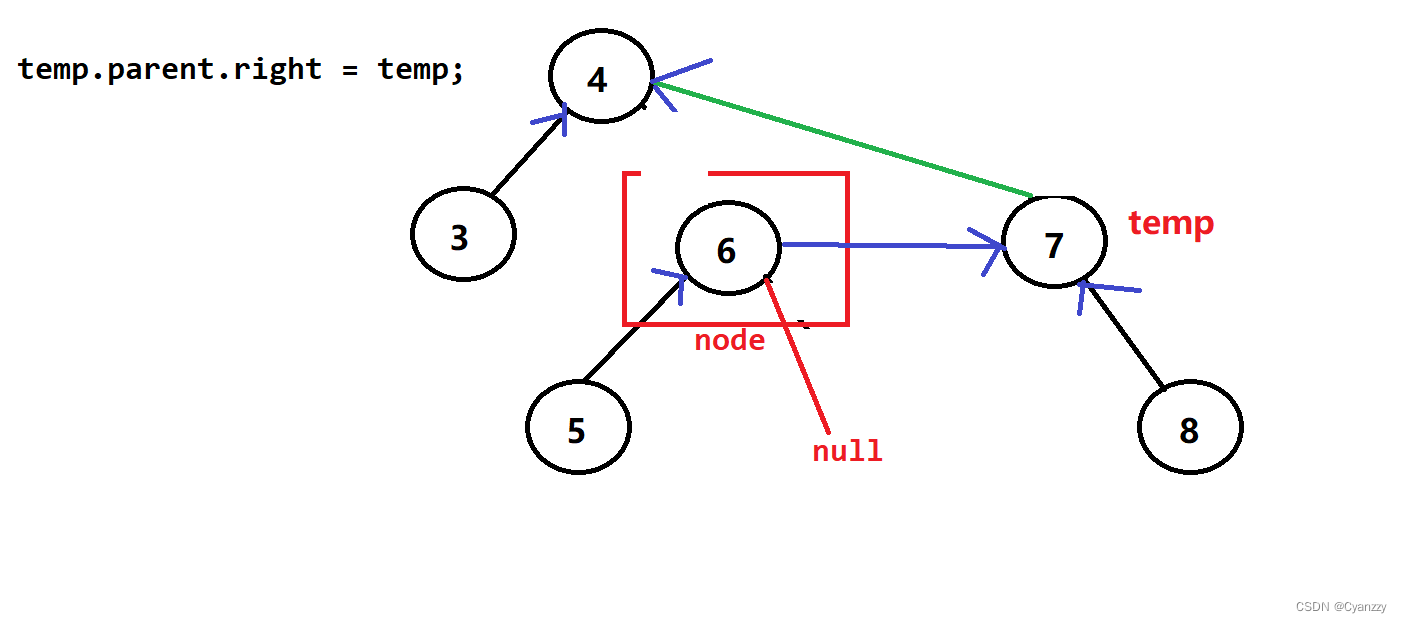
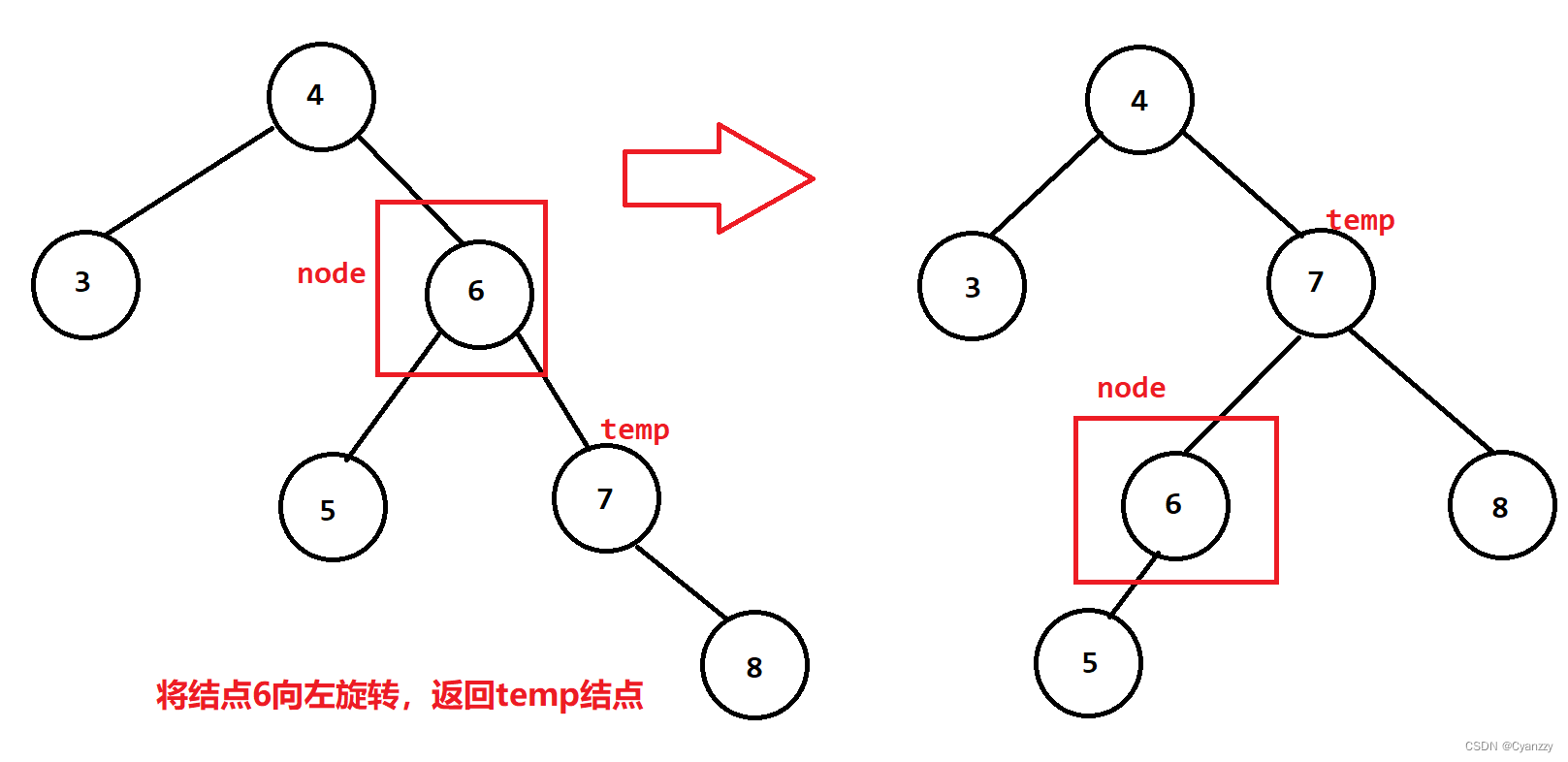
在这里插入图片描述

/**
 * 向左旋转
 *
 * @param node 待旋转的结点
 * @return 旋转后取代被提供节点的节点
 */
protected Node rotateLeft(Node node) {

    /*保存待旋转结点的右孩子，将其右孩子node父节点上准备取代node结点*/
    // temp指向node右孩子
    Node temp = node.right;
    // temp的父亲结点变成node的父亲结点
    temp.parent = node.parent;

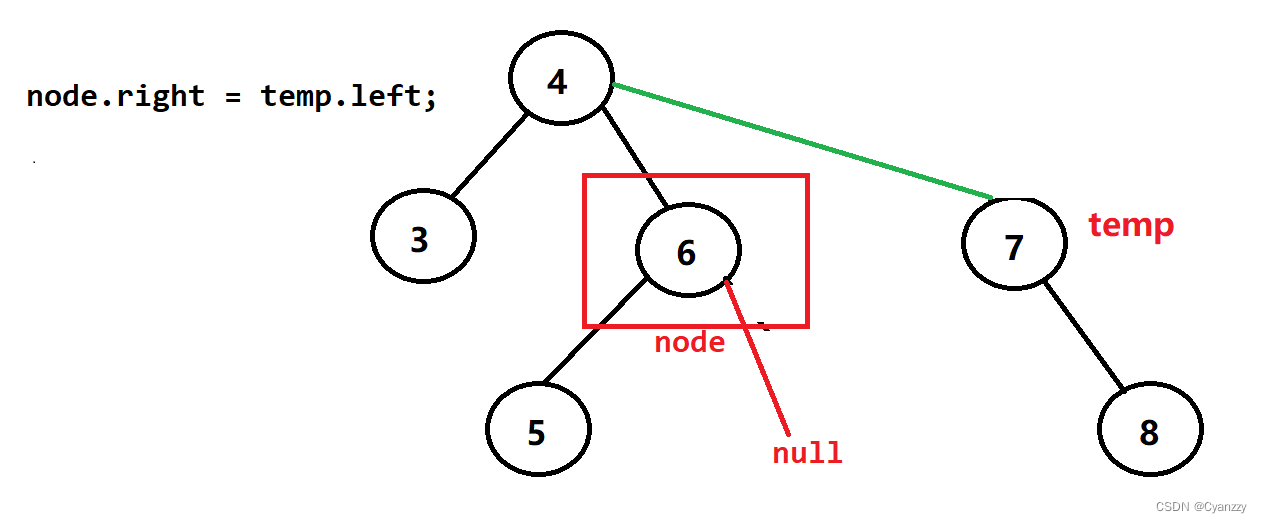
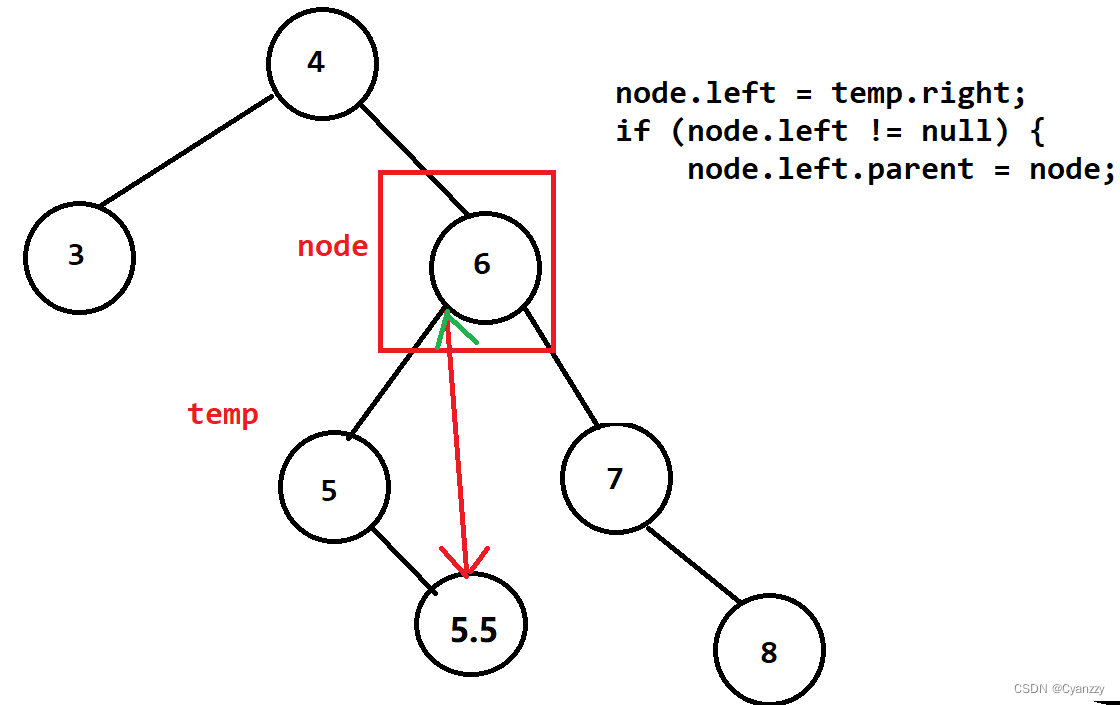
    /*temp要代替node，temp的左孩子挂在node右孩子上*/
    // node的右孩子指向temp的左孩子
    node.right = temp.left;
    if (node.right != null) {
        node.right.parent = node;
    }

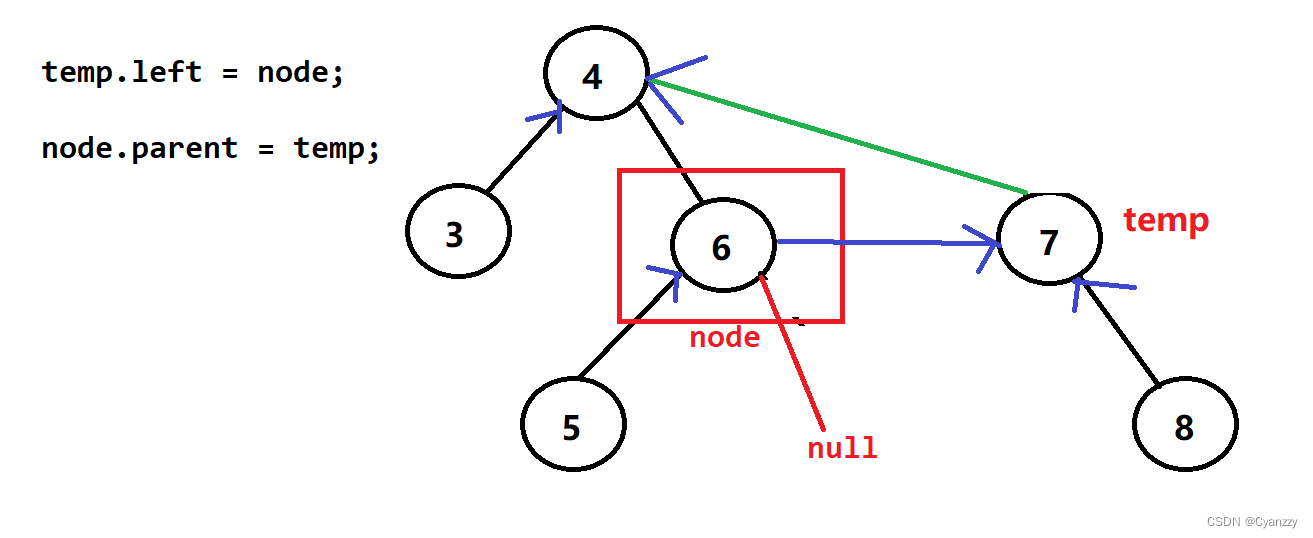
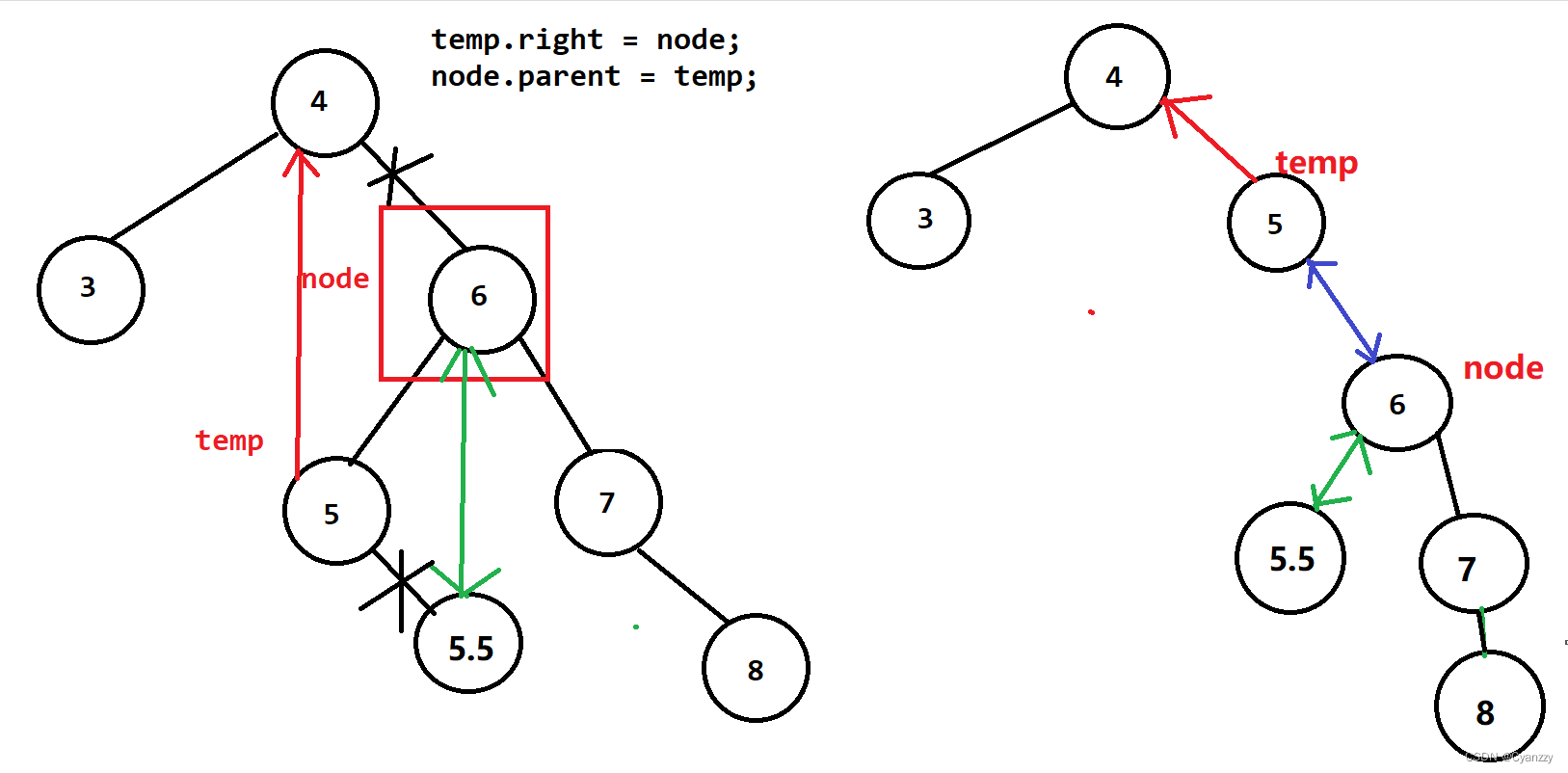
    /*将node挂在temp左孩子下面*/
    // temp左孩子指向node
    temp.left = node;
    //node的父亲指向temp
    node.parent = temp;

    /*temp取代了node的位置，
    node若是原父亲结点的左孩子，则原父亲结点左指针指向temp，
    node若是原父亲结点的右孩子，则原父亲结点的右指针指向temp*/
    if (temp.parent != null) {
        // 如果node是temp父亲结点的左孩子
        if (node == temp.parent.left) {
            // temp父亲结点的左孩子变成temp（相当于temp代替node位置）
            temp.parent.left = temp;
        } else { // 如果node是temp父亲结点的右孩子
            // temp父亲结点的右孩子变成temp（相当于temp代替node位置）
            temp.parent.right = temp;
        }
    } else {
        root = temp;
    }

    return temp;
}

右旋转

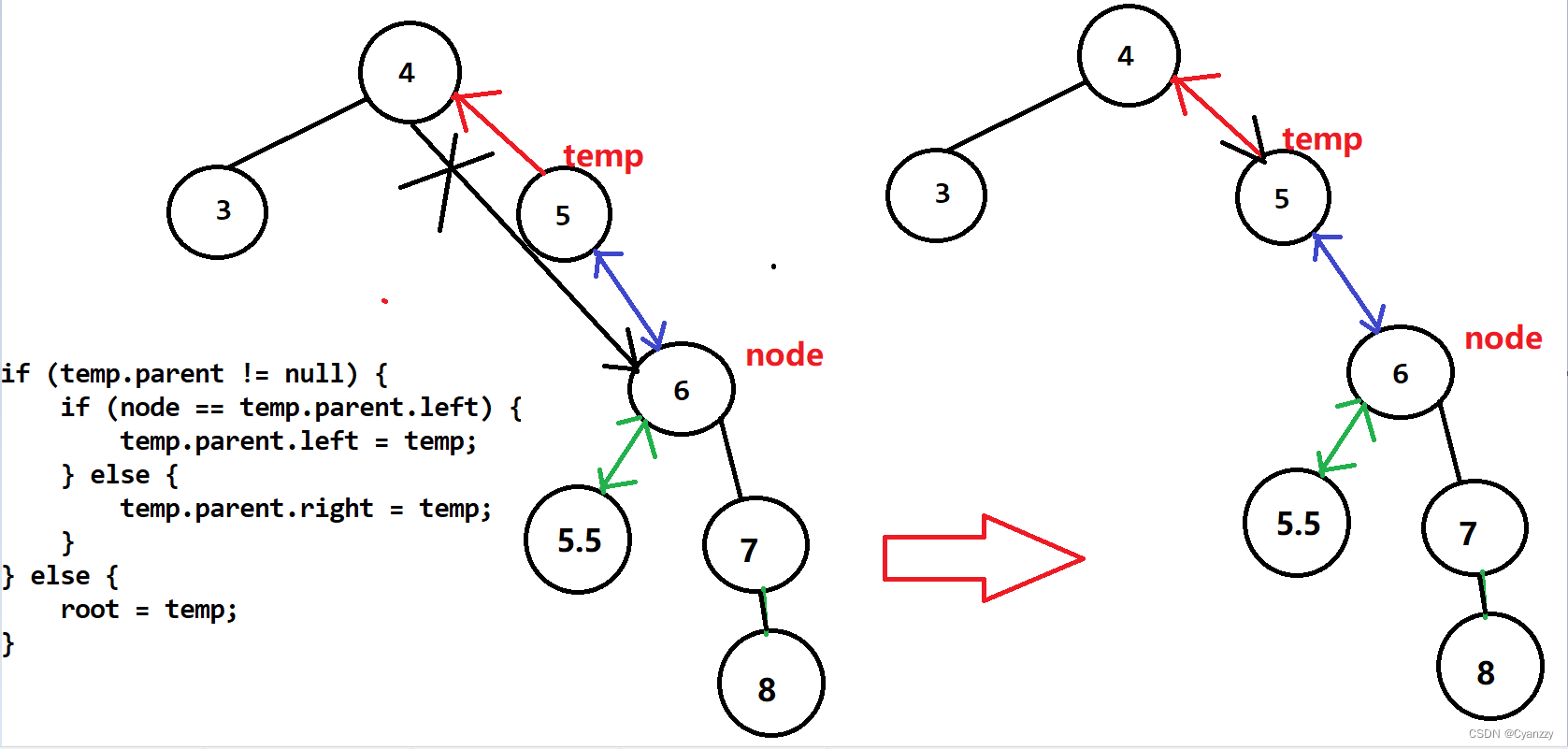
在这里插入图片描述

/**
 * 向右旋转
 *
 * @param node 待旋转的结点
 * @return 旋转后取代被提供节点的节点
 */
protected Node rotateRight(Node node) {

    /*保存待旋转结点的左孩子，将左孩子挂在node结点的父亲结点上，准备取代node结点*/
    // 向右旋转记住左孩子
    Node temp = node.left;
    // node左孩子的父亲指向node的父亲
    temp.parent = node.parent;

    /*temp要代替node，temp的右孩子挂在node左孩子上*/
    // node左孩子指向temp右孩子
    node.left = temp.right;
    if (node.left != null) {
        node.left.parent = node;
    }

    /*将node挂在temp右孩子下面*/
    // temp的右孩子指向node
    temp.right = node;
    // node的parent指向temp
    node.parent = temp;

    /*temp取代了node的位置，
    node若是原父亲结点的左孩子，则原父亲结点左指针指向temp，
    node若是原父亲结点的右孩子，则原父亲结点的右指针指向temp*/
    if (temp.parent != null) {
        if (node == temp.parent.left) {
            temp.parent.left = temp;
        } else {
            temp.parent.right = temp;
        }
    } else {
        root = temp;
    }
    return temp;
}

AVL Tree

性质

根结点的左、右子树高度之差的绝对值不超过1
且根结点左子树和右子树仍然是AVL树。

平衡因子 BF

一个结点的左子树与右子树的高度之差。
AVL树中的任意结点的BF只可能是-1，0和1。
AVL树的ASL可保持在 $O (l o g 2 n)$

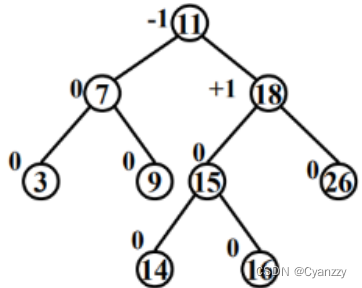
在这里插入图片描述

对于包含n个结点的AVL树，其最坏情况下的查找、插入和删除操作时间复杂度均为 $O (l o g n)$

结点结构

/**
 *AVL结点结构
 */
protected static class AVLNode extends Node {
    public int height;

    public AVLNode(int value, Node parent, Node left, Node right) {
        super(value, parent, left, right);
    }
}

创建结点

/**
 * 创建结点
 * @param value
 *            结点的值
 * @param parent
 *            结点的父亲结点
 * @param left
 *            结点的左孩子结点
 * @param right
 *            结点的右孩子结点
 * @return
 */
@Override
protected Node createNode(int value, Node parent, Node left, Node right) {
    return new AVLNode(value, parent, left, right);
}

插入结点

/**
 * 添加结点
 * 插入结点后要保证平衡性
 * @param element 待插入的元素
 * @return newNode
 */
@Override
public Node insert(int element) {
    Node newNode = super.insert(element);
    rebalance((AVLNode)newNode);
    return newNode;
}

删除结点

删除叶子结点，直接删除，依次向上调整成AVL树
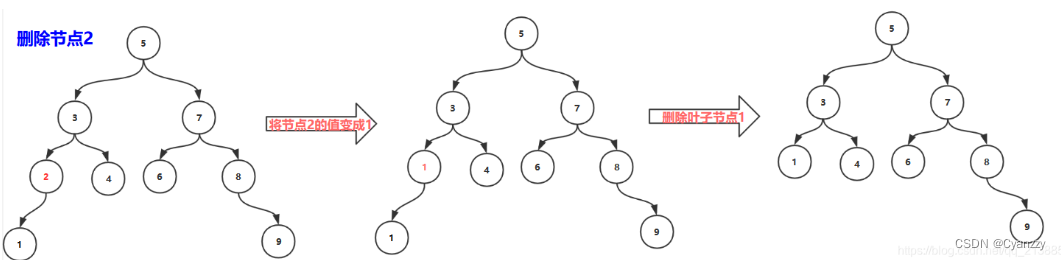
删除非叶子结点且结点只有左孩子，该结点值替换成左孩子值，然后删除左孩子结点
删除非叶子结点且结点只有右孩子，该结点值替换成右孩子值，然后删除左孩子结点
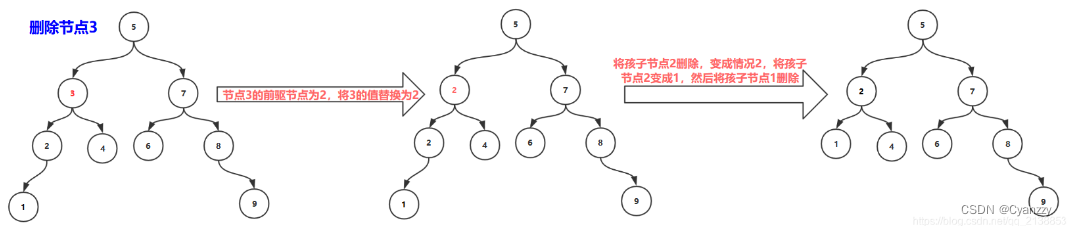
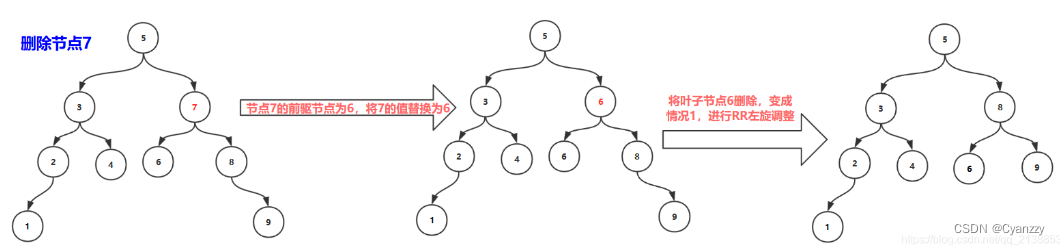
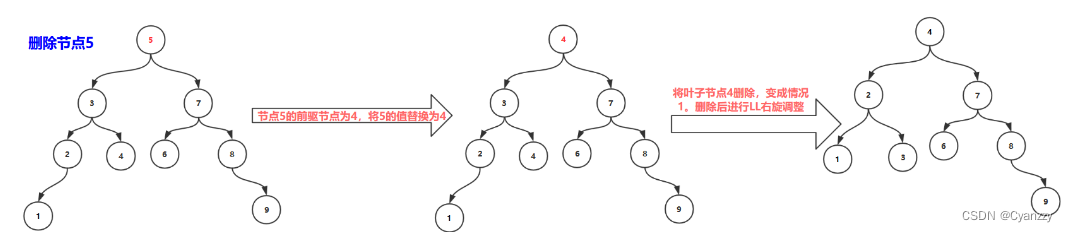
删除非叶子结点，该结点既有左孩子也有右孩子。该结点值替换为该结点的前驱结点（或者后继结点），然后删除前驱结点（或者后继结点）

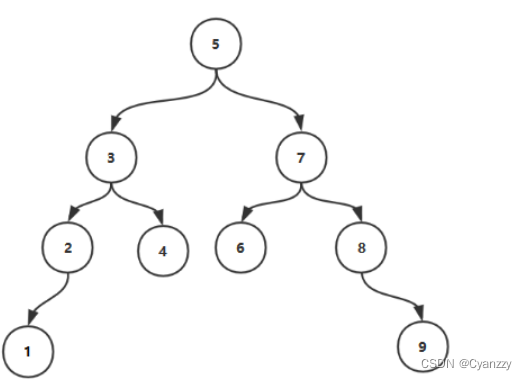
在这里插入图片描述

第一种情况

删除叶子节点1,节点9,节点4,节点6

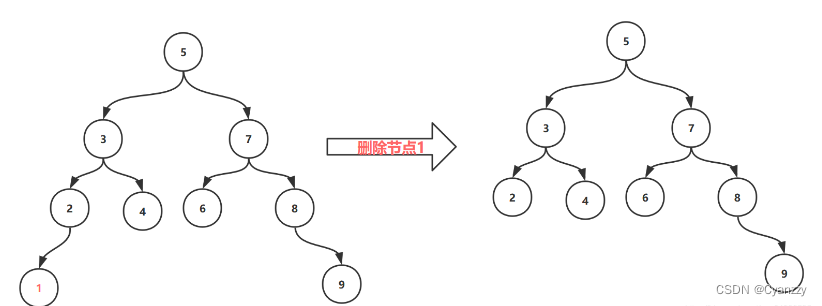
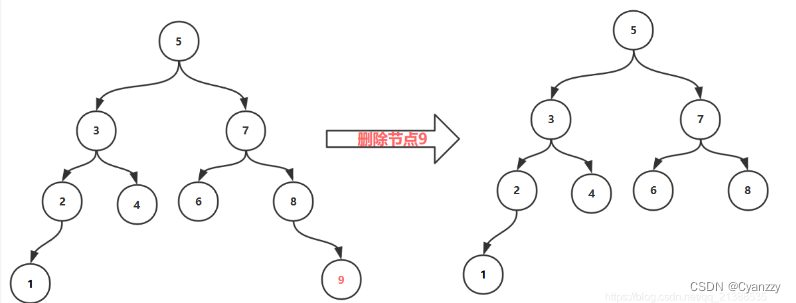
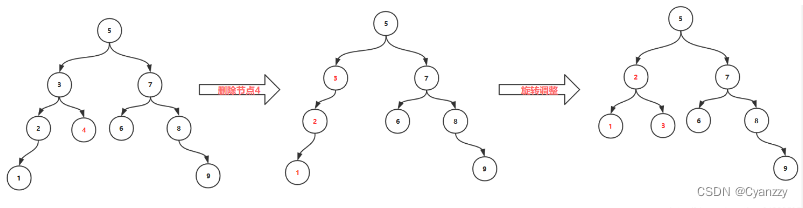
在这里插入图片描述

第二种情况

删除非叶子节点，该节点只有左孩子

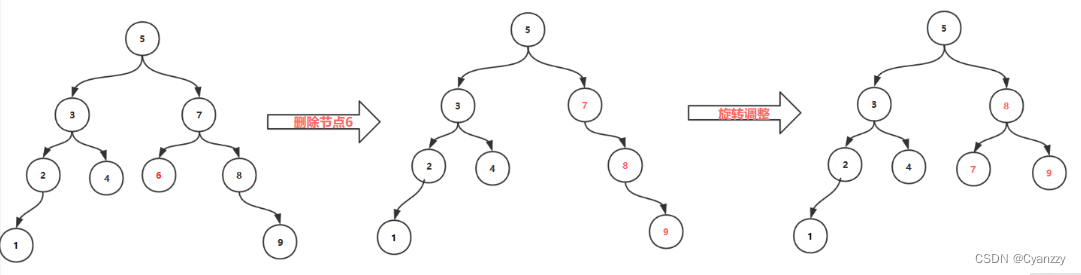
在这里插入图片描述

第三种情况

删除非叶子节点，该节点只有右孩子

在这里插入图片描述

第四种情况

删除非叶子节点（节点3，节点7，节点5），非叶子节点既有左孩子，又有右孩子

在这里插入图片描述

/**
 * 删除结点
 * @param element
 *            待移除结点的值
 *
 * @return 代替删除结点的结点
 */
@Override
public Node delete(int element) {
    // 查找待删除结点的位置
    Node deleteNode = super.search(element);
    if (deleteNode != null) {
        // 待删除结点存在删除它并用新结点取代
        Node successorNode = super.delete(deleteNode);
        if (successorNode != null) {
            // if replaced from getMinimum(deleteNode.right) then come back there and update heights
            // 如果取代待删除结点的新结点右子树非空，minimum为successorNode右子树的最左边结点，
            // 如果取代待删除结点的新结点右子树不存在，minimum为successorNode
            AVLNode minimum = successorNode.right != null ? (AVLNode)getMinimum(successorNode.right) : (AVLNode)successorNode;
            // 重新计算minimum高度
            recomputeHeight(minimum);
            // 重新调整minimum为根结点的树
            rebalance((AVLNode)minimum);
        } else {
            recomputeHeight((AVLNode)deleteNode.parent);
            rebalance((AVLNode)deleteNode.parent);
        }
        return successorNode;
    }
    // 如果没找到待删除的结点，直接返回null
    return null;
}

平衡调整

向AVL树插入结点可能造成不平衡，此时要调整树的结构，使之重新达到平衡

在一棵AVL树上插入结点可能会破坏树的平衡性，需要平衡化处理恢复平衡，且保持BST的结构性质。若用Y表示新插入的结点，A表示离新插入结点Y最近的，且平衡因子变为±2的祖先结点。

LL型：新结点Y 被插入到 A 的左子树的左子树上（顺）
RR型：新结点Y 被插入到 A 的右子树的右子树上（逆）
LR型：新结点Y 被插入到 A 的左子树的右子树上（逆、顺）
RL型：新结点Y 被插入到 A 的右子树的左子树上（顺、逆）

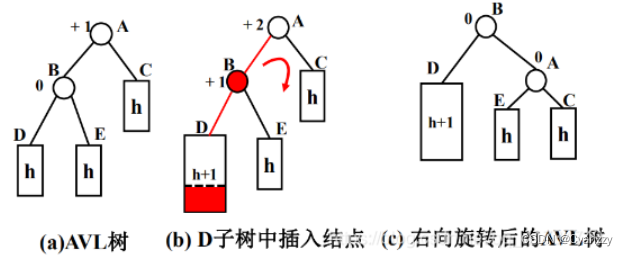
LL型

1.LL型：新结点Y 被插入到 A 的左子树的左子树上（顺）

在这里插入图片描述

/**
 * LL型
 * 向右旋转
 * @param node 待旋转的结点
 */
private Node avlRotateRight(Node node) {
    // 待旋转结点的左子树的根结点
    Node temp = super.rotateRight(node);

    updateHeight((AVLNode)temp.right);
    updateHeight((AVLNode)temp);
    return temp;
}

RR型

2.RR型：新结点Y 被插入到 A 的右子树的右子树上（逆）

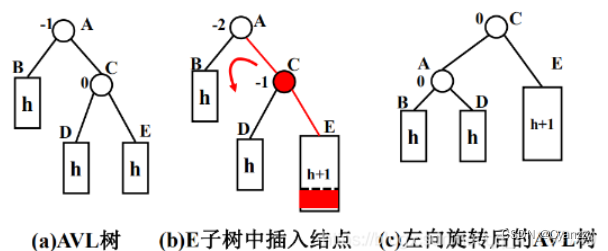
在这里插入图片描述

/**
 * RR型
 * 向左旋转
 * @param node 待旋转的结点
 * @return
 */
private Node avlRotateLeft(Node node) {
    //待旋转结点的右子树的根结点
    Node temp = super.rotateLeft(node);

    updateHeight((AVLNode)temp.left);
    updateHeight((AVLNode)temp);
    return temp;
}

LR型

3.LR型：新结点Y 被插入到 A 的左子树的右子树上(逆,顺)

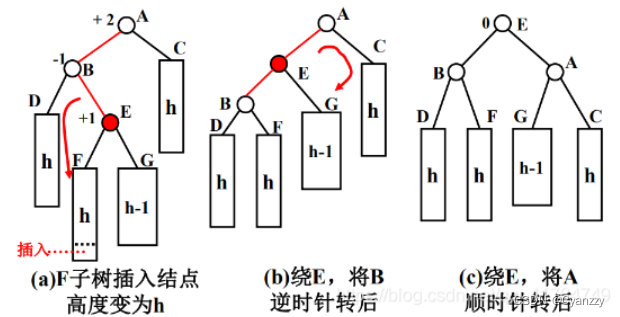
在这里插入图片描述

/**
 * LR型
 * @param node 待调整树的根结点
 * @return node左孩子为根结点的树先向左旋转，然后以node为根结点的树向右旋转
 */
protected Node doubleRotateLeftRight(Node node) {
    node.left = avlRotateLeft(node.left);
    return avlRotateRight(node);
}

RL型

4.RL型：新结点Y 被插入到 A 的右子树的左子树上(顺, 逆)

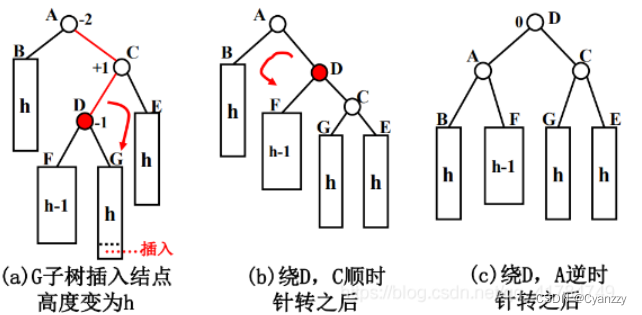
在这里插入图片描述

/**
 * RL型
 * @param node 待调整树的根结点
 * @return node右孩子为根结点的树先向右旋转，然后以node为根结点向左旋转
 */
protected Node doubleRotateRightLeft(Node node) {
    node.right = avlRotateRight(node.right);
    return avlRotateLeft(node);
}

调整

重新计算node到所有父结点的高度

/**
 * 重新计算从node节点到所有父结点的高度信息。需要在删除后完成。
 * @param node
 */
private void recomputeHeight(AVLNode node) {
    while (node != null) {
        node.height = maxHeight((AVLNode)node.left, (AVLNode)node.right) + 1;
        node = (AVLNode)node.parent;
    }
}

计算两个子树的最大高度

/**
 * 计算最大高度
 * @param node1 根结点1
 * @param node2 根结点2
 * @return 返回两个结点为根结点的树最大高度
 */
private int maxHeight(AVLNode node1, AVLNode node2) {
    if (node1 != null && node2 != null) {
        return node1.height > node2.height ? node1.height : node2.height;
    } else if (node1 == null) {
        return node2 != null ? node2.height : -1;
    } else if (node2 == null) {
        return node1 != null ? node1.height : -1;
    }
    return -1;
}

更新树的高度

/**
 * 更新node为根结点树的高度
 *
 * @param node 其高度和平衡性需要更新的结点
 */
private static final void updateHeight(AVLNode node) {
    int leftHeight = (node.left == null) ? -1 : ((AVLNode) node.left).height;
    int rightHeight = (node.right == null) ? -1 : ((AVLNode) node.right).height;
    node.height = 1 + Math.max(leftHeight, rightHeight);
}

调整函数

/**
 * 从插入的节点向上移动，并根据需要更新高度和平衡信息。
 * 如果某个节点的平衡达到2或-2，则意味着必须重新平衡该子树。
 *
 * @param node 插入的结点
 */
private void rebalance(AVLNode node) {
    while (node != null) {

        // 保存node的父结点
        Node parent = node.parent;

        // node结点左子树的高度
        int leftHeight = (node.left == null) ? -1 : ((AVLNode) node.left).height;
        // node结点右子树的高度
        int rightHeight = (node.right == null) ? -1 : ((AVLNode) node.right).height;
        // 平衡因子
        int nodeBalance = rightHeight - leftHeight;
        // rebalance (-2 means left subtree outgrow, 2 means right subtree)
        if (nodeBalance == 2) { // 右子树高些
            if (node.right.right != null) { // RR型
                node = (AVLNode)avlRotateLeft(node);
                break;
            } else { // RL型
                node = (AVLNode)doubleRotateRightLeft(node);
                break;
            }
        } else if (nodeBalance == -2) { // 左子树高些
            if (node.left.left != null) { // LL型
                node = (AVLNode)avlRotateRight(node);
                break;
            } else { // LR型
                node = (AVLNode)doubleRotateLeftRight(node);
                break;
            }
        } else {
            updateHeight(node);
        }

        // node指向其父结点，继续调整
        node = (AVLNode)parent;
    }
}

Size Balanced Tree

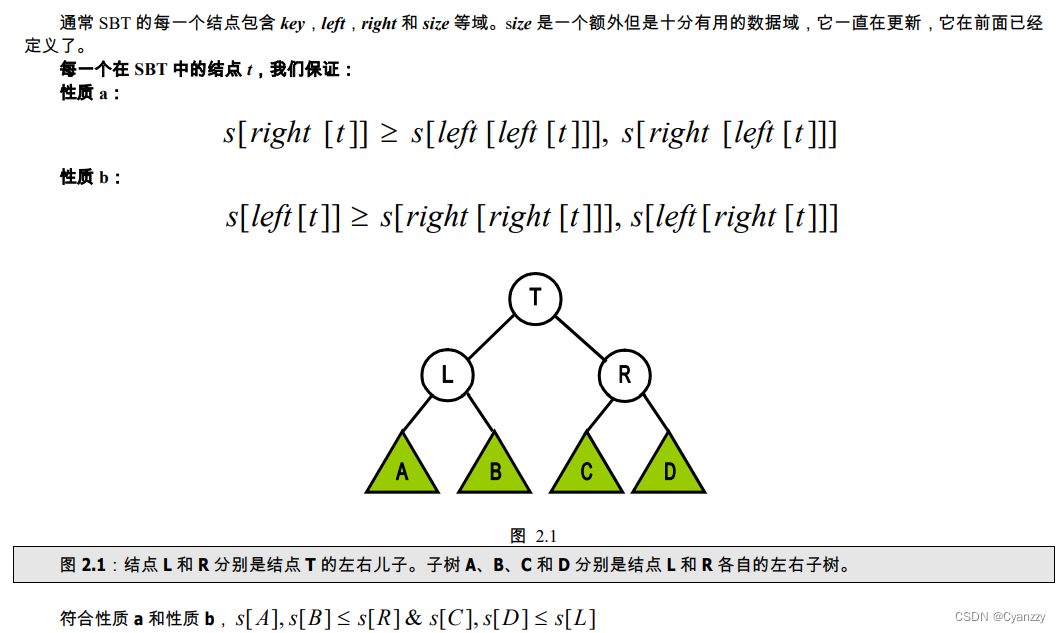
在这里插入图片描述

即每棵子树的大小不小于其兄弟的子树大小

HashMap

结点结构

public static class SBTNode<K extends Comparable<K>, V> {
    public K key;
    public V value;
    public SBTNode<K, V> left;
    public SBTNode<K, V> right;
    public int size;

    public SBTNode(K key, V value) {
        this.key = key;
        this.value = value;
        size = 1;
    }
}

右旋转 LL型

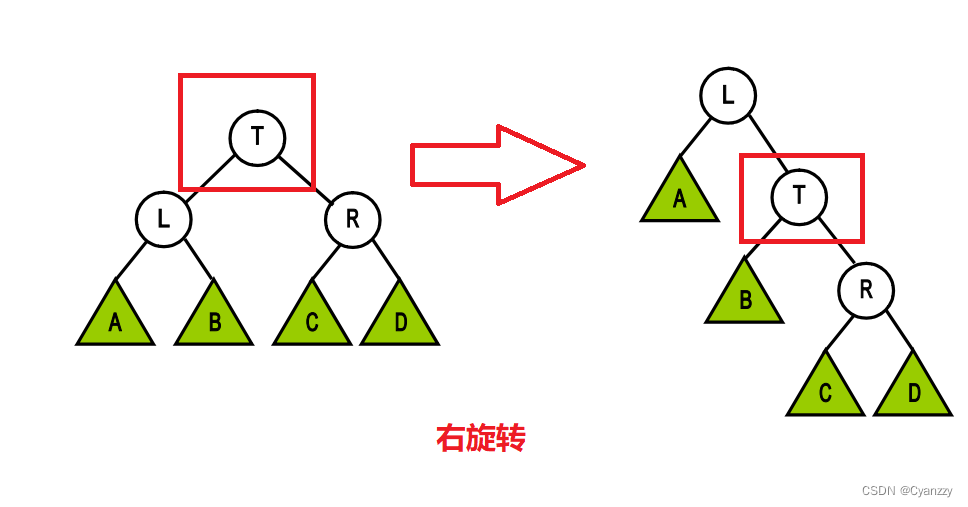
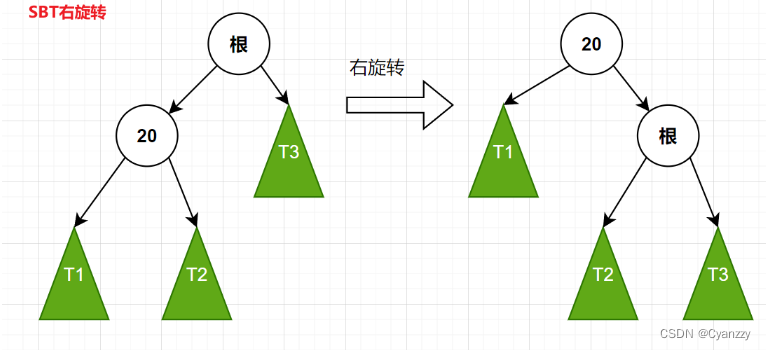
在这里插入图片描述

T1-T3，表示子树，另外两个表示节点，旋转之后T1和T2和T3这三颗子树下面的节点是没有发生改变，也就是说T1-T3不需要再次计算size
只需要计算上图那两个白色的节点的size即可！
旋转之后，新的根节点的节点数是原根节点的节点数，
计算旋转之后，原根节点的节点数=该节点的左子树节点数+右子树的节点数+自己本身

/**
 * 右旋转
 * @param node 准备旋转的结点
 * @return
 */
private SBTNode<K, V> rightRotate(SBTNode<K, V> node) {
    /*右旋转*/
    // leftNode指向node左孩子
    SBTNode<K, V> leftNode = node.left;
    // leftNode的右孩子挂在node左孩子下
    node.left = leftNode.right;
    //node挂在leftNode右孩子上
    leftNode.right = node;

    /*旋转之后，新的根节点的节点数，还应该是原根节点的节点数，
    所以最后我们只需要计算旋转之后，原根节点的节点数即可，
    = 该节点的左子树节点数+右子树的节点数+自己本身*/
    // 新的根结点结点数
    leftNode.size = node.size;
    // 原根结点的结点数
    node.size = (node.left != null ? node.left.size : 0) + (node.right != null ? node.right.size : 0) + 1;
    return leftNode;
}

左旋转 RR型

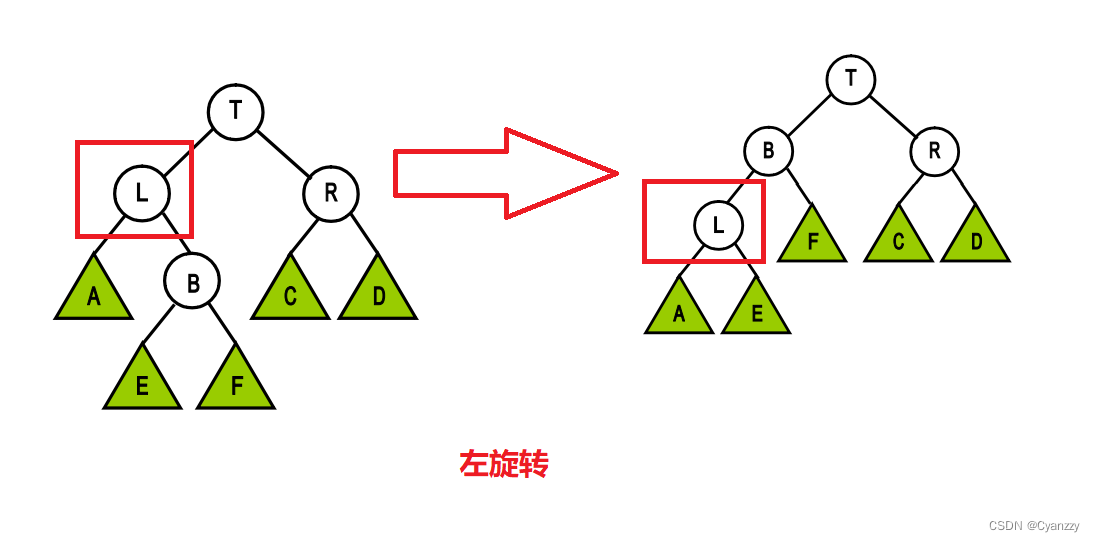
在这里插入图片描述

/**
 * 左旋转 RR型
 * @param node 待旋转的结点
 * @return
 */
private SBTNode<K, V> leftRotate(SBTNode<K, V> node) {
    /*左旋转*/
    //rightNode指向node右孩子
    SBTNode<K, V> rightNode = node.right;
    //rightNode的左孩子挂在node右孩子下面
    node.right = rightNode.left;
    //node变成rightNode的左孩子
    rightNode.left = node;

     /*旋转之后，新的根节点的节点数，还应该是原根节点的节点数，
    所以最后我们只需要计算旋转之后，原根节点的节点数即可，
    = 该节点的左子树节点数+右子树的节点数+自己本身*/
    // 新的根结点结点数
    rightNode.size = node.size;
    // 原根结点的结点数
    node.size = (node.left != null ? node.left.size : 0) + (node.right != null ? node.right.size : 0) + 1;
    return rightNode;
}

假设A节点需要进行LR型的旋转，则只需A.left = 左旋转一次，再A= 右旋转一次。
同理，假设B节点需要进行RL型的旋转，则只需B.right = 右旋转一次，再B = 左旋转一次。

maintain

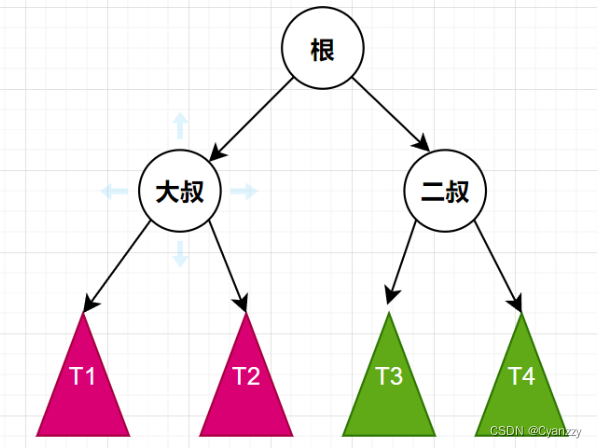
在这里插入图片描述

LL型：T1的size > 二叔的size
LR型：T2的size > 二叔的size
RL型：T3的size > 大叔的size
RR型：T4的size > 大叔的size

叔叔的节点数，必须大于等于侄子的节点数。不然的话，就需要进行平衡调整

/**
 * 调整平衡
 * @param node
 * @return
 */
private SBTNode<K, V> matain(SBTNode<K, V> node) {
    //node为空，不调整
    if (node == null) {
        return null;
    }
    /*值得注意的是，旋转操作之后，还需要递归调用Maintain方法。递归调用的对象，就是：哪个节点的子树被换了，则需要调用这个Maintain（新子树）*/
    /*递归调用Maintain时，一定是先调用cur的左右子树，然后才是调用cur。因为cur的处理，是依赖于他的左右孩子的。*/
    if (node.left != null && node.left.left != null && node.right != null && node.left.left.size > node.right.size) { //LL型
        // 右旋转
        node = rightRotate(node);

        node.right = matain(node.right);
        node = matain(node);
    } else if (node.left != null && node.left.right != null && node.right != null && node.left.right.size > node.right.size) { // LR型
        /*假设A节点需要进行LR型的旋转，则只需A.left = 左旋转一次，再A= 右旋转一次。*/
        node.left = leftRotate(node.left);
        node = rightRotate(node);

        node.left = matain(node.left);
        node.right = matain(node.right);
        node = matain(node);
    } else if (node.right != null && node.right.right != null && node.left != null && node.right.right.size > node.left.size) { // RR型
        // 左旋转
        node = leftRotate(node);

        node.left = matain(node.left);
        node = matain(node);
    } else if (node.right != null && node.right.left != null && node.left != null && node.right.left.size > node.left.size) { //RL型
        /*假设B节点需要进行RL型的旋转，则只需B.right = 右旋转一次，再B = 左旋转一次。*/
        node.right = rightRotate(node.right);
        node = leftRotate(node);

        node.left = matain(node.left);
        node.right = matain(node.right);
        node = matain(node);
    }
    return node;
}

插入结点

/**
 * 插入操作
 * @param node 待插入的结点
 * @param key
 * @param value
 * @return
 */
private SBTNode<K, V> add(SBTNode<K, V> node, K key, V value) {
    if (node == null) {
        return new SBTNode<>(key, value);
    } else {
        // 沿途节点的节点数加1
        node.size++;
        if (key.compareTo(node.key) < 0) {
            node.left = add(node.left, key, value);
        } else {
            node.right = add(node.right, key, value);
        }
        // 调整平衡
        return matain(node);
    }
}

删除结点

/**
 * 删除结点
 * @param node 待删除的结点
 * @param key
 * @return
 */
private SBTNode<K, V> delete(SBTNode<K, V> node, K key) {
    // 沿途节点的节点数-1
    node.size--;
    if (key.compareTo(node.key) > 0) {
        node.right = delete(node.right, key);
    } else if (key.compareTo(node.key) < 0) {
        node.left = delete(node.left, key);
    } else {
        if (node.left == null && node.right == null) { // node是叶子结点
            // free node memory -> C++
            node = null;
        } else if (node.left == null && node.right != null) { // node只有右子树
            // free node memory -> C++
            node = node.right;
        } else if (node.left != null && node.right == null) { // node只有左子树
            // free node memory -> C++
            node = node.left;
        } else { // node左右子树都有
            // des的前驱结点
            SBTNode<K, V> pre = null;
            // 向右子树查找最左边的结点
            SBTNode<K, V> des = node.right;
            des.size--;
            /*找到右子树最左边的结点*/
            while (des.left != null) {
                pre = des;
                des = des.left;
                // 最终的des结点重新计算结点数
                des.size--;
            }

            if (pre != null) {
                pre.left = des.right;
                // 将node结点替换成des结点
                des.right = node.right;
            }
            // 连接node原先的左子树
            des.left = node.left;
            des.size = des.left.size + des.right.size + 1;
            // free node memory -> C++
            node = des;
        }
    }
    /*假设当前SBT树的高度是H，现在删除一个节点后，高度可能还是H，又或者是H- 1。
    此时调整平衡与不调整平衡，都不影响后续的操作。*/
    return node;
}

红黑树

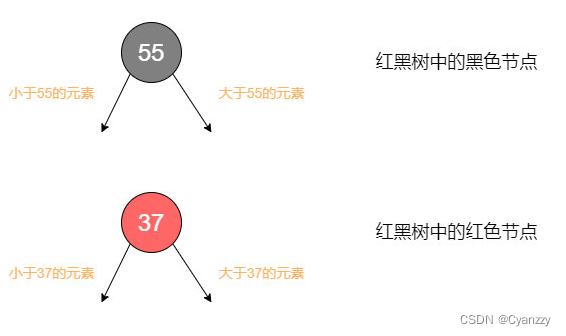
性质：红黑树是具有下列性质的二叉查找树

结点包含颜色信息（黑色或红色）
根结点是黑色
所有叶子结点都是黑色
每个红色结点的子结点必须是黑色
从任一结点到其每个叶子节点的所有简单路径必须包含相同数目的黑色结点

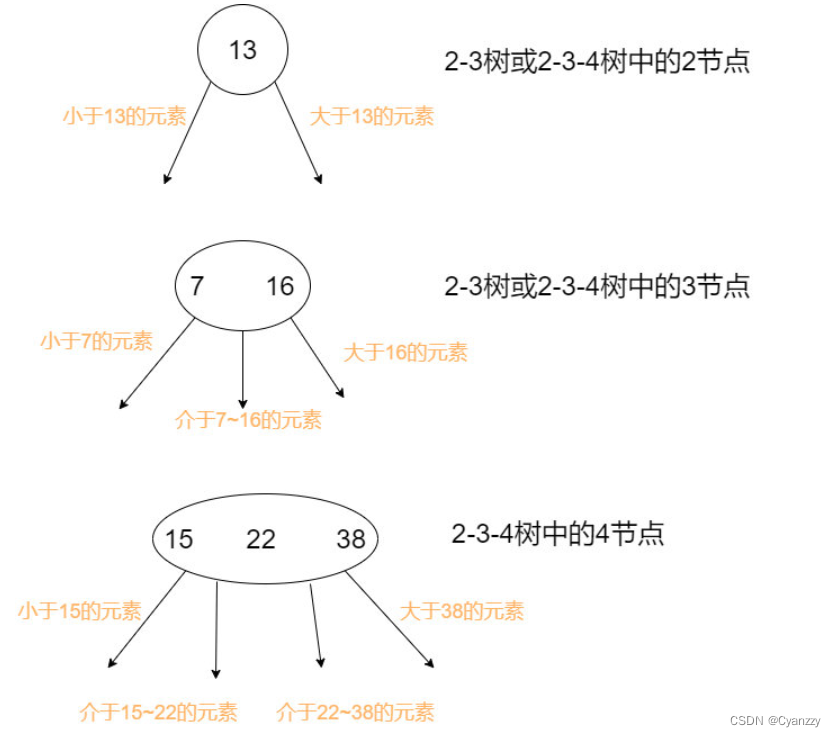
在这里插入图片描述

2-3-4树

2节点中存放着一个key[X]，两个指针，分别指向小于X的子节点和大于X的子节点；
3节点中存放在两个key[X,Y],三个指针，分别指向小于X的子节点，介于X~Y之间的子节点和大于Y的子节点
4节点可依此类推。

在这里插入图片描述

2-3-4树到红黑树转化

红黑树是对概念模型2-3-4树的一种实现，由于直接进行不同节点间的转化会造成较大的开销，所以选择以二叉树为基础，在二叉树的属性中加入一个颜色属性来表示2-3-4树中不同的节点。
2-3-4树中的2节点对应着红黑树中的黑色节点
2-3-4树中的非2节点是以红节点+黑节点的方式存在
红节点的意义是与黑色父节点结合，表达着2-3-4树中的3，4节点。

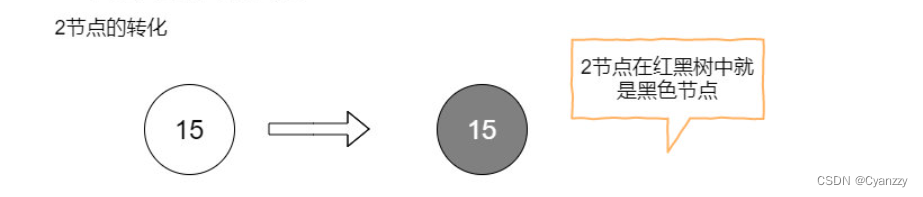
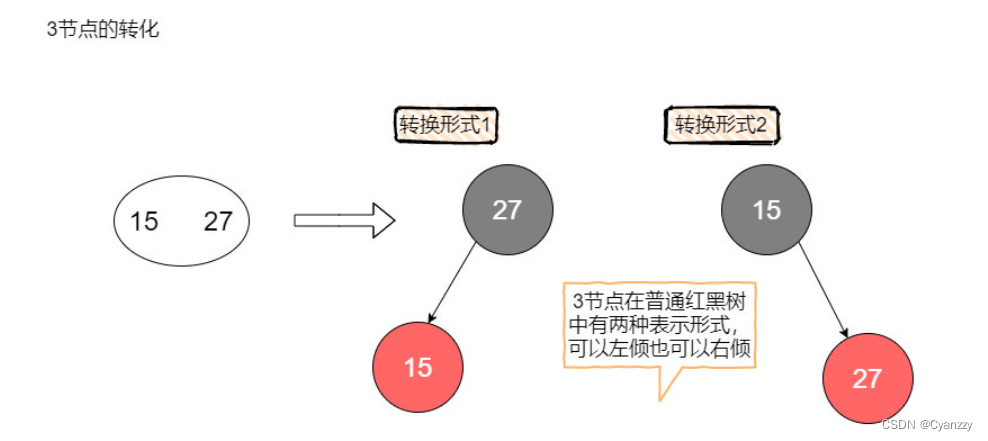
结点转化

2节点直接转化为黑色节点
3节点这里可以有两种表现形式，左倾红节点或者右倾红节点
4节点被强制要求转化为一个黑父带着左右两个红色儿子。

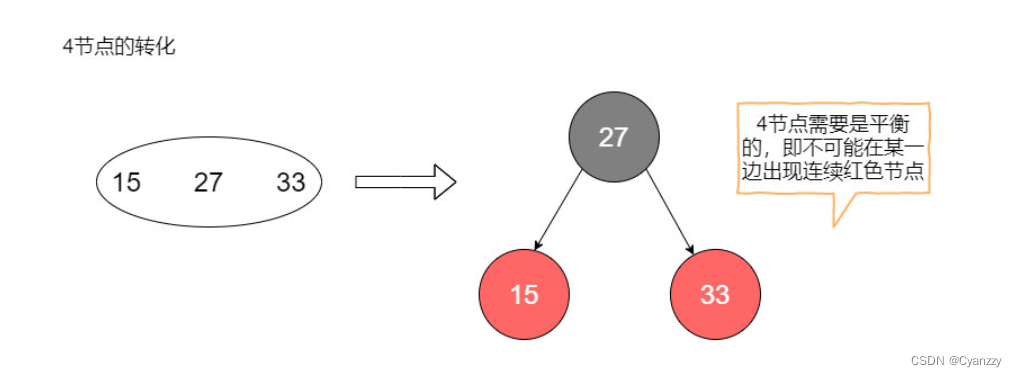
在这里插入图片描述

2-3树到红黑树转化

研究主体是2-3树（原因会在后文给出），并且是2-3树中较为特殊的一种转化–左倾红黑树。

左倾红黑树限制了如果在树中出现了红色节点，那么这个节点必须是左儿子。

结点转化

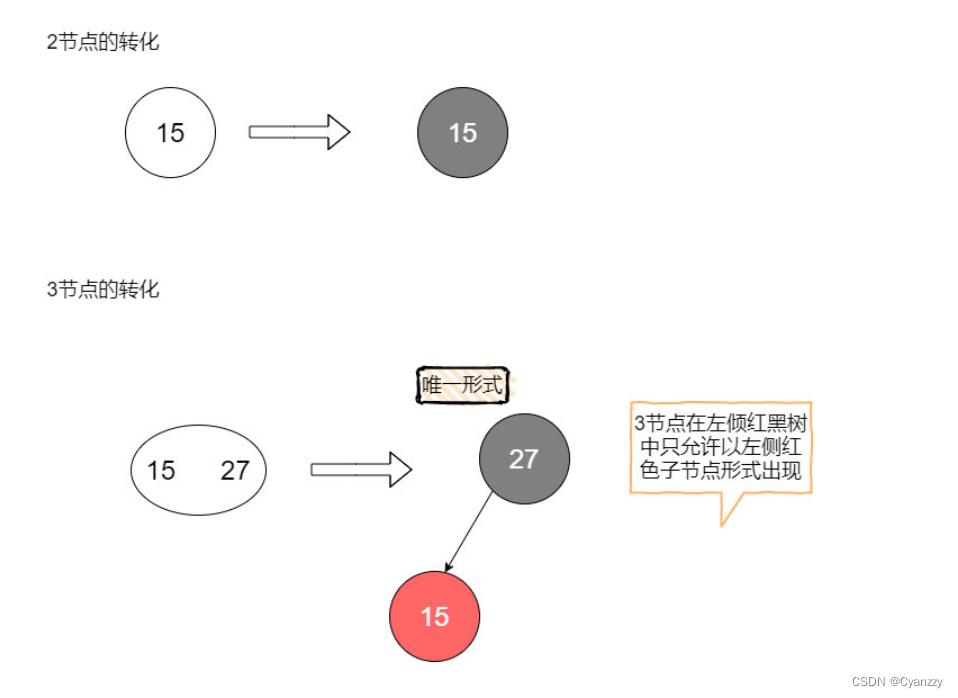
在这里插入图片描述

红黑树转2-3树

把左倾红黑树中的红色节点顺时针方向旋转45°使其与黑父平行，然后再将它们看作一个整体，就是一颗2-3树

在这里插入图片描述

基于2-3树实现的红黑树

算法导论中给出的是红黑树基于2-3-4树实现，其中4节点要求平衡（即4节点必须用黑色父亲和左右两个红色儿子表示，红色儿子不能出现在同一边）。

定义：一颗2-3查找树或者一颗空树，由以下两种节点组合而成：

2-节点：节点内有一个数值域，还有两个存放左右孩子节点的内存地址的区域。左孩子节点的数值比当前节点小，右孩子节点的数值比当前节点大。
3-节点：节点内有两个数值域，还有三个存放孩子节点的内存地址的区域。左孩子节点的数值都是小于该节点的，右孩子的数值都是大于该节点的，中间孩子的数值在该节点两个数值的中间。

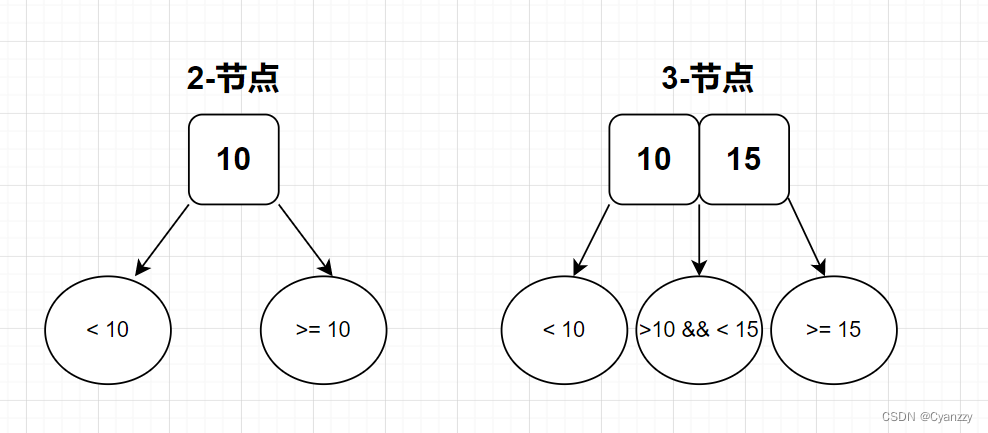
2-3树的插入操作

先将这个元素尝试性地放在已经存在的节点中
如果要存放的节点是2节点，那么插入后会变成3节点
如果要存放的节点是3节点，那么插入后会变成4节点（临时）
然后，我们对可能生成的临时4节点进行分裂处理，使得临时4节点消失。

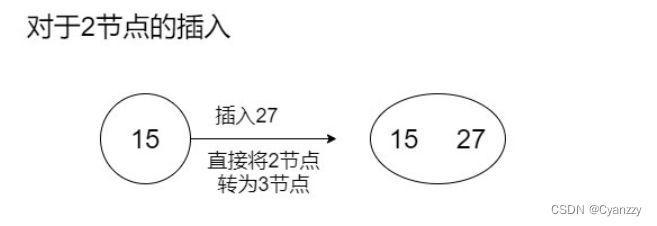
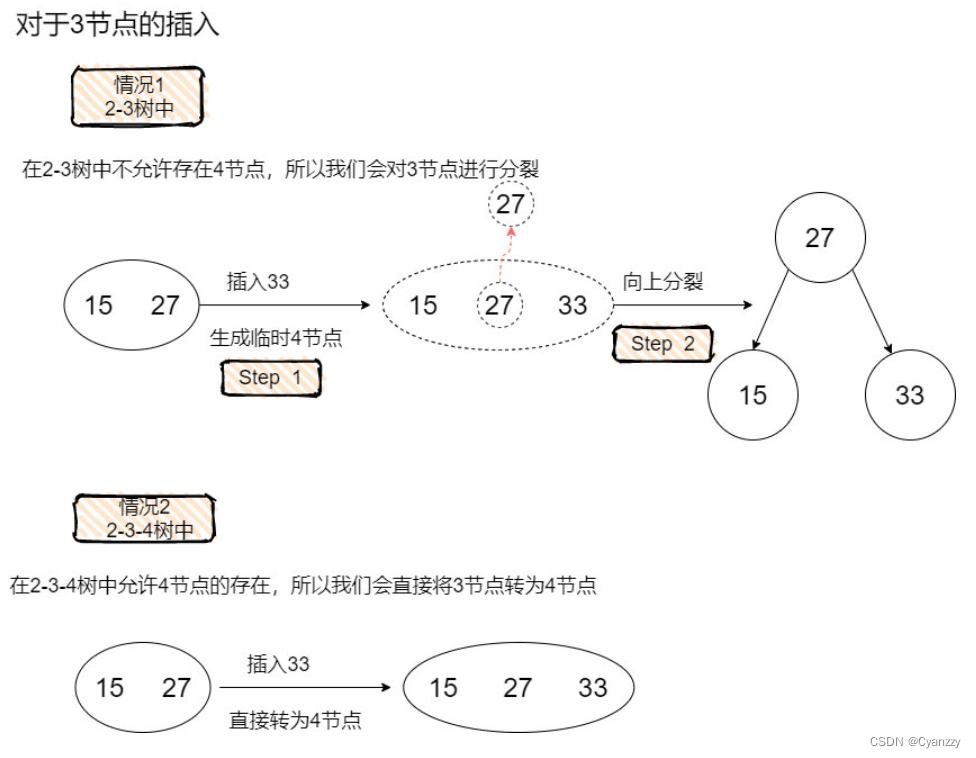
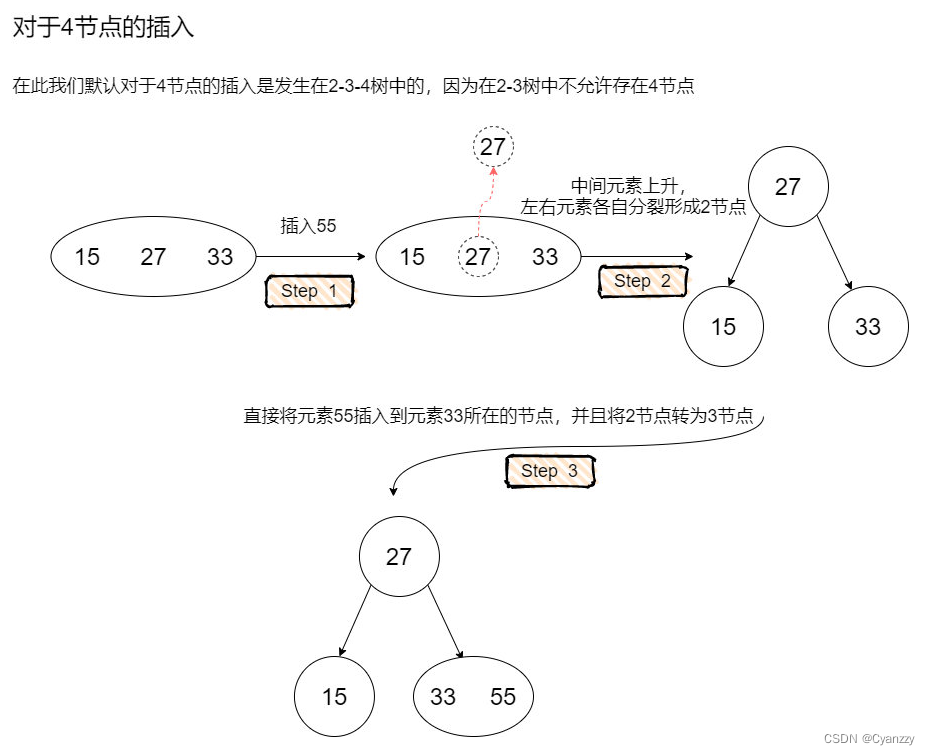
在这里插入图片描述

2-3树的删除操作

对于2-3树的删除我们主要要考虑待删除元素在2节点这种情况，因为如果待删除元素在3节点，那么可以直接将这个元素删除，而不会破坏2-3树的任何性质（删除这个元素不会引起高度的变化）。
当待删除元素在2节点的时候，由于删除这个元素会导致2节点失去自己唯一的元素，引发2节点自身的删除，会使得树中某条路径的高度发生变化，树变得不平衡。

解决方案

先删除2结点，然后平衡调整2-3树
让被删除结点的元素不可能出现在2结点

选方案2

在搜索到这个节点的路径中，不断地判断当前节点是否为2节点，
如果是，就从它的兄弟节点或者它的父节点借一个元素，使得当前节点由2节点成为一个3节点或者一个临时4节点

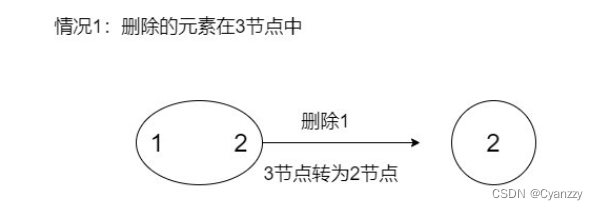
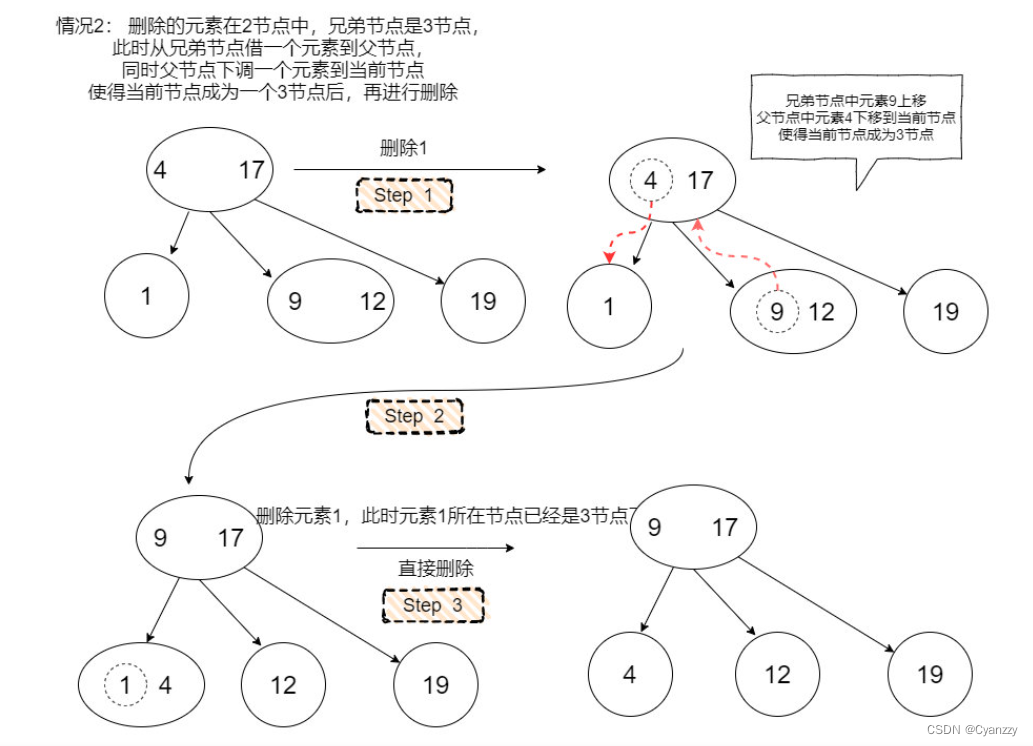
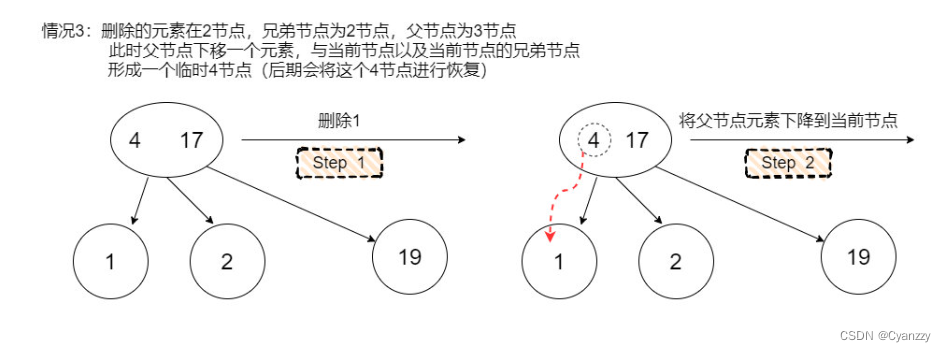
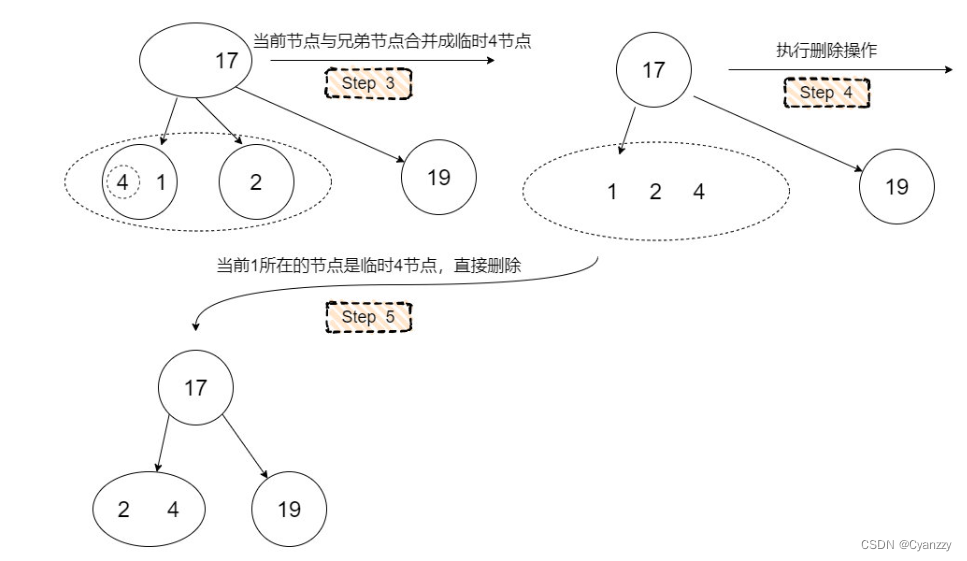
在这里插入图片描述

左倾红黑树的插入操作

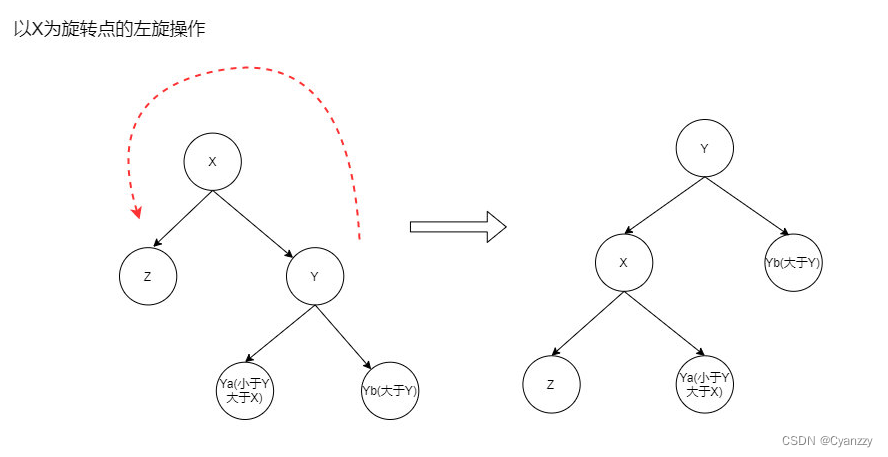
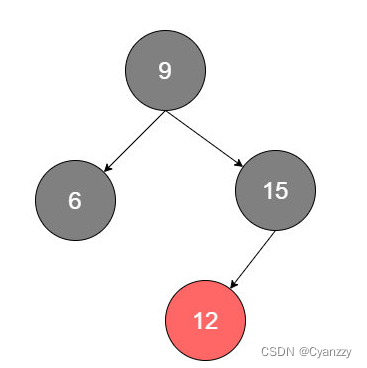
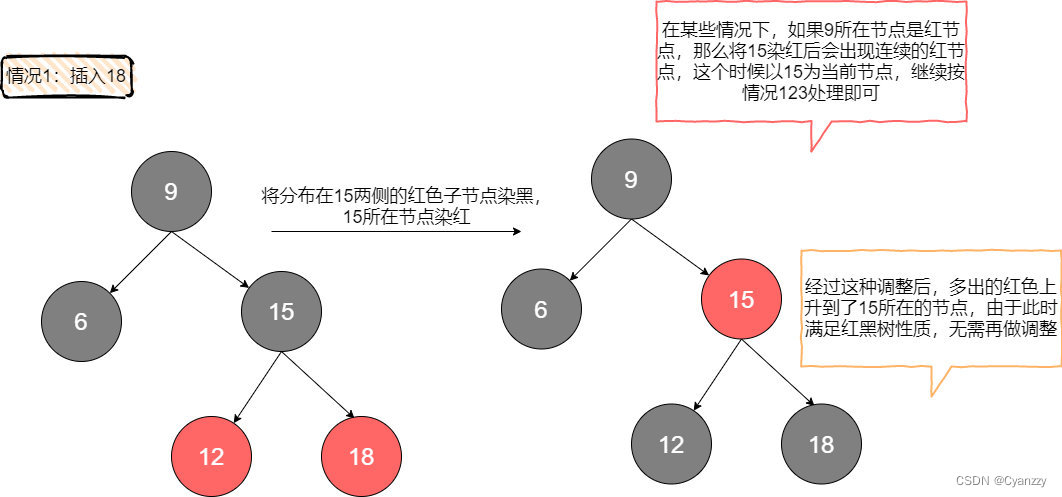
在这里插入图片描述

情况1

待插入元素比黑色父亲大，插在黑色父亲的右边，黑色父亲左边是红色儿子

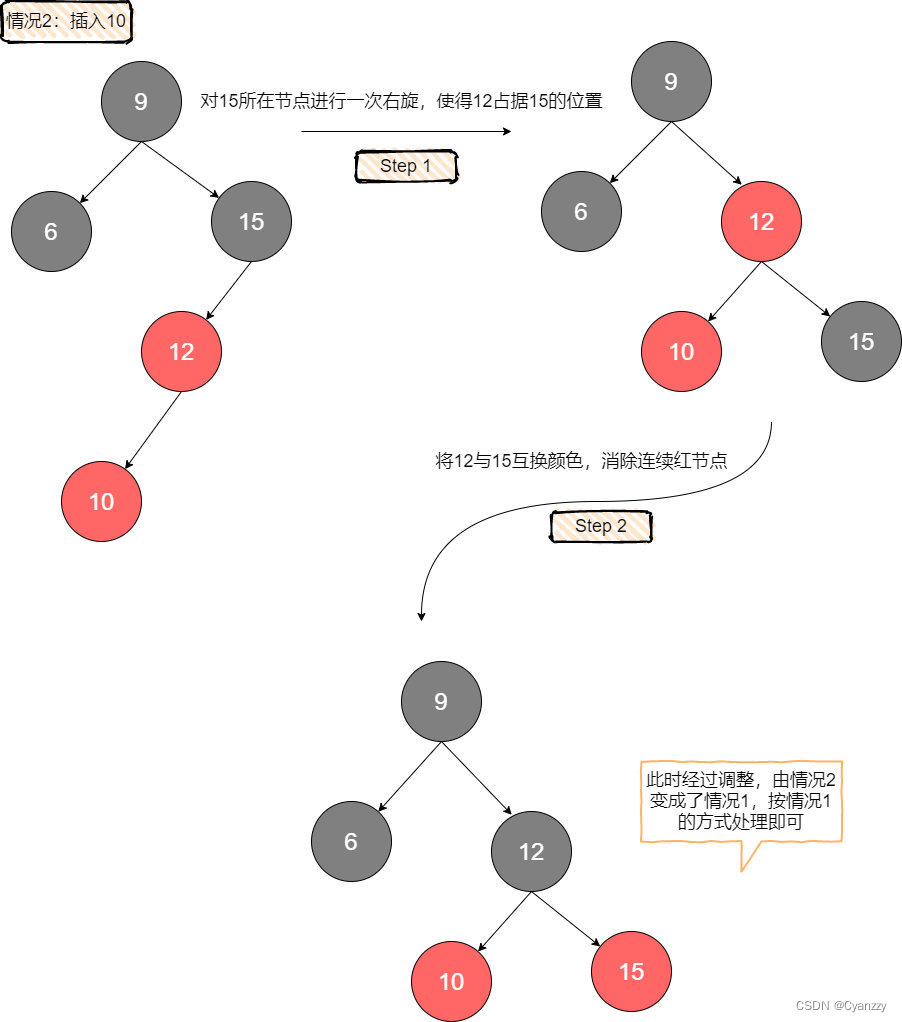
在这里插入图片描述

情况2

待插入元素比红色父亲小，且红色父亲自身左倾

在这里插入图片描述

情况3

待插入元素比红色父亲大，且红色父亲自身左倾

在这里插入图片描述

左倾红黑树的删除操作

当我们要删除某个节点的时候选择它的前驱节点或者后继节点元素来替代它，转而删除它的前驱/后继节点。

从当前的根节点出发，利于2-3树中预合并的策略逐层对红黑树进行调整。
具体的做法是，每次都保证当前的节点是2-3树中的非2节点，如果当前节点已经是非2节点，那么直接跳过
如果当前节点是2节点，那么根据兄弟节点的状况来进行调整：
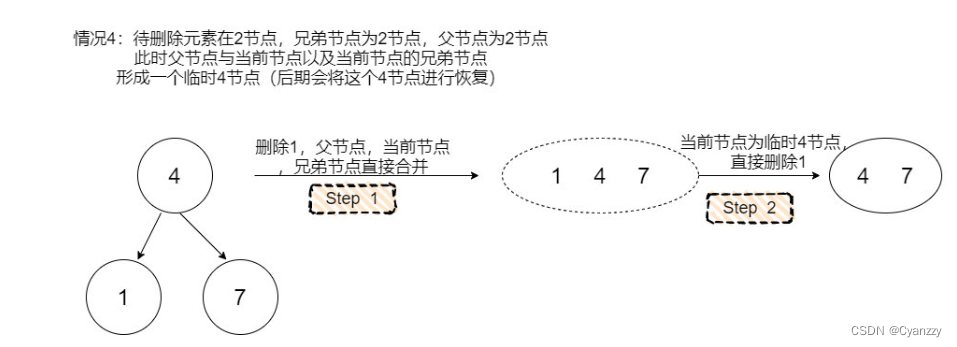
如果兄弟是2节点，那么从父节点借一个元素给当前节点，然后与兄弟节点一起形成一个临时4节点。
如果兄弟是非2节点，那么兄弟上升一个元素到父节点，同时父节点下降一个元素到当前节点，使得当前节点成为一个3节点。

这样的策略能够保证最后走到待删除节点的时候，它一定是一个非2节点，我们可以直接将其元素删除。

删除工作

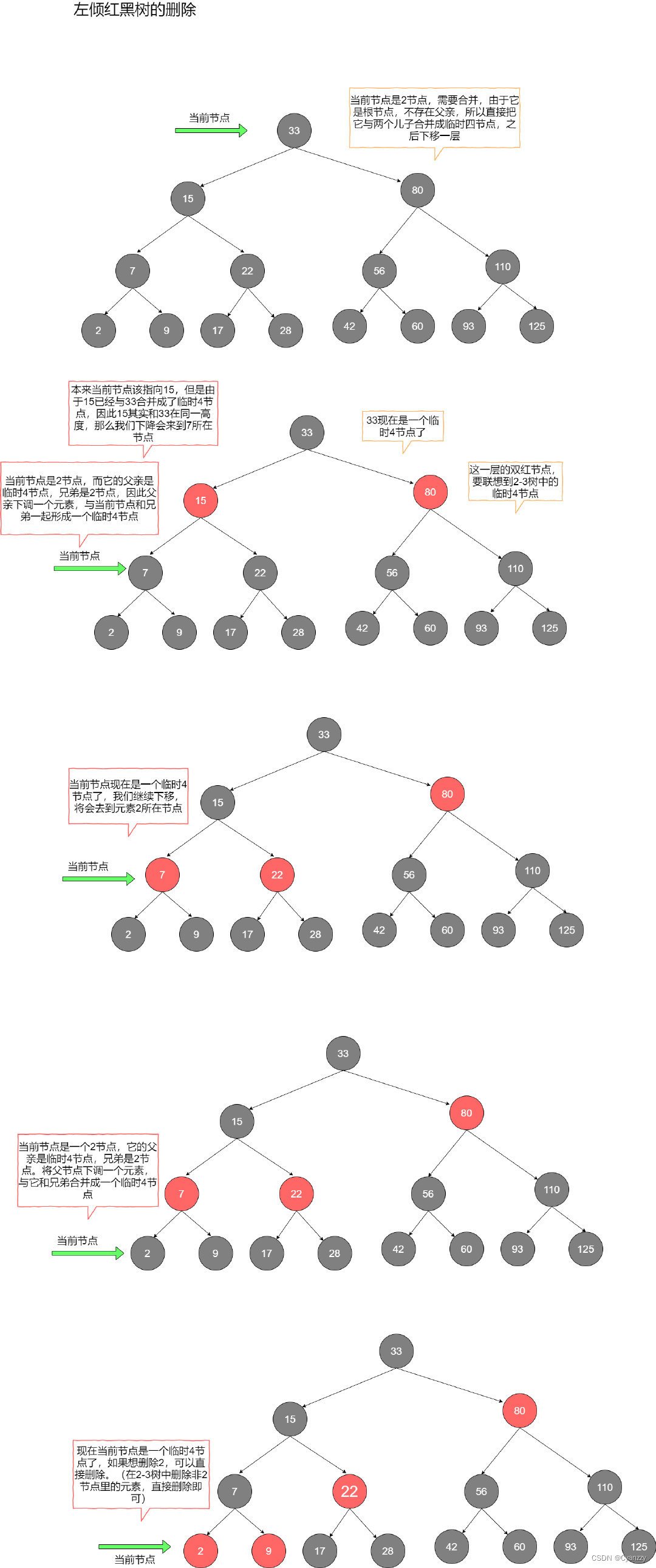
在这里插入图片描述

由于红黑树定义的限制，我们在调整的过程中出现了一些本不该存在的红色右倾节点
于是我们顺着搜索的方向向上回溯，如果遇到当前节点具备右倾的红色儿子，那么对当前节点进行一次左旋
这时原本的右儿子会来到当前节点的位置，然后将右儿子与当前节点交换颜色，我们就将右倾红节点修复成了左倾红节点，同时我们并没有破坏黑色节点的平衡。

基于2-3-4实现的红黑树

哨兵：哑对象，简化边界条件的处理

黑高：从某个结点x出发（不含该结点）到达一个结点的任意一条简单路径上的黑色结点数称为该结点的黑高，红黑树的黑高是根结点的黑高

性质1 每个结点都是红色或黑色
性质2 根结点是黑色
性质3 每个叶子结点是黑色
性质4 一个结点红色，则它两个子结点都是黑色
性质5 对于每个结点，从该结点到所有后代叶结点的简单路径上，均包含相同数目的黑色结点

旋转

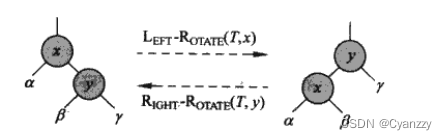
在这里插入图片描述

左旋转

当某个结点在x上左旋，假设它的右孩子是y而不是T.nil
x可以是其右孩子不是T.nil结点的树内任意节点
左旋以x到y的链为支轴，使y成为该子树新的根结点，x成为y的左孩子，y的左孩子成为x的右孩子

/**
 * 左旋转
 * @param node 待旋转的结点
 * @return
 */
@Override
protected Node rotateLeft(Node node) {
    /*temp取代node成为该子树的新的根结点*/
    //temp指向x的右孩子（y）
    Node temp = node.right;
    //temp的父亲变成node的父亲取代node
    temp.parent = node.parent;

    /*将temp的左孩子挂在node的右孩子上*/
    //将temp的左孩子变成node右孩子
    node.right = temp.left;
    //如果node右孩子不是叶子结点，就将上边temp左孩子的父亲变成node
    if (node.right != nilNode) {
        node.right.parent = node;
    }

    /*将node挂在temp左孩子下面*/
    //node变成temp的左孩子
    temp.left = node;
    //node的父亲变成temp
    node.parent = temp;

    // node原先是其父亲结点的哪个孩子，就把temp作为node父亲结点的哪个孩子，temp取代node位置
    if (temp.parent != nilNode) { //当temp有父亲结点时
        //如果node是其原父亲结点的左孩子，那么其父亲结点左指针指向temp
        if (node == temp.parent.left) {
            temp.parent.left = temp;
        } else { //如果node是其原父亲结点的右孩子，那么其父亲结点右指针指向temp
            temp.parent.right = temp;
        }
    } else { //当temp没有父亲结点，直接将其作为根结点
        root = temp;
    }

    return temp;
}

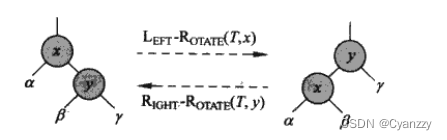
在这里插入图片描述

右旋转

当某个结点在y上右旋，假设它的左孩子是x而不是T.nil
y可以是其左孩子不是T.nil结点的树内任意节点
右旋以y到x的链为支轴，使x成为该子树新的根结点，y成为x的右孩子，x的右孩子成为y的左孩子

/**
 * 右旋转
 * @param node 待旋转的结点
 * @return
 */
@Override
protected Node rotateRight(Node node) {
    /*temp取代node成为该子树的新的根结点*/
    //temp指向node左孩子
    Node temp = node.left;
    //temp的父亲变成node的父亲，
    // 但node父亲的孩子指针还是指向node，后续会转移
    temp.parent = node.parent;

    /*将temp的右孩子挂在node的左孩子上*/
    //将temp的右孩子变成node左孩子
    node.left = temp.right;
    //如果node左孩子不是叶子结点，就将上边temp右孩子的父亲变成node
    if (node.left != nilNode) {
        node.left.parent = node;
    }

    /*将node挂在temp右孩子下面*/
    //node变成temp的右孩子
    temp.right = node;
    //node的父亲变成temp
    node.parent = temp;

    // node原先是其父亲结点的哪个孩子，就把temp作为node父亲结点的哪个孩子，temp取代node位置
    // 更新原先node父亲结点的孩子指针
    if (temp.parent != nilNode) {
        //如果node是其原父亲结点的左孩子，那么其父亲结点左指针指向temp
        if (node == temp.parent.left) {
            temp.parent.left = temp;
        } else { //如果node是其原父亲结点的右孩子，那么其父亲结点右指针指向temp
            temp.parent.right = temp;
        }
    } else {
        root = temp;
    }

    return temp;
}

插入操作

类似于搜索二叉树插入方法，将结点z插入到红黑树中
将z着色红色
调整红黑树，保持红黑树性质

/**
 * 插入结点
 * @param element
 * @return
 */
@Override
public Node insert(int element) {
    Node newNode = super.insert(element);
    newNode.left = nilNode;
    newNode.right = nilNode;
    root.parent = nilNode;
    insertRBFixup((RedBlackNode) newNode);
    return newNode;
}

a.插入后的结点z，由于z和它的父结点z.parent都是红色，违反了性质（如果一个结点是红色的，其两个子结点都是黑色的），由于叔叔结点y是红色的，应用情况1。结点被重新着色，并且指针z沿树上升，所得树如b

在这里插入图片描述

b.再一次z及其父结点都是红色，但叔叔结点y是黑色，z是其父结点的右孩子，可以应用情况2.执行一次左旋后，得到c

在这里插入图片描述

c.现在z是其父结点的左孩子，可以应用情况3重新着色并执行一次右旋得到d

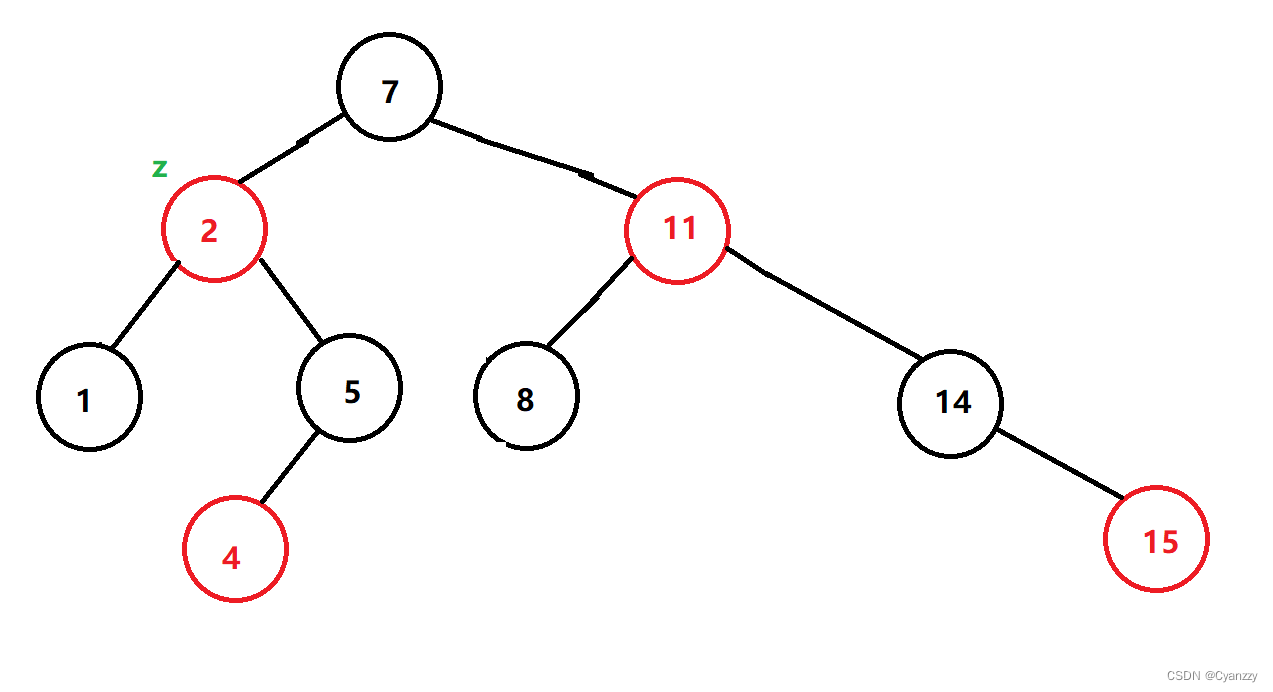
在这里插入图片描述

d.此时红黑树合法

由于新插入的红色结点的两个子结点都是哨兵，性质1、3、5成立
性质2 根结点为黑色可能会破坏
性质4 红结点不能有红色孩子可能会破坏

代码实现

/**
 * 在插入结点后调整红黑树，使红黑树保持性质
 * Restores Red-Black tree properties after insert if needed. Insert can
 * break only 2 properties: root is red or if node is red then children must
 * be black.
 * @param currentNode
 */
private void insertRBFixup(RedBlackNode currentNode) {
    // current node is always RED, so if its parent is red it breaks
    // Red-Black property, otherwise no fixup needed and loop can terminate
    /*
        每次while循环开头保持三个不变式
        1. 结点currentNode是红结点
        2. 如果currentNode.parent是根结点，那么它黑色
        3. 如果有任何红黑性质被破坏，至多一条性质被破坏
        * 性质2被破坏 原因是currentNode是根结点且是红结点
        * 性质4被破坏 原因是currentNode和currentNode.parent都是红结点
    * */
    while (currentNode.parent != root && ((RedBlackNode) currentNode.parent).color == ColorEnum.RED) { //当currentNode的父结点是红色时
        //currentNode的父亲结点
        RedBlackNode parent = (RedBlackNode) currentNode.parent;
        //currentNode的爷爷结点
        RedBlackNode grandParent = (RedBlackNode) parent.parent;
        if (parent == grandParent.left) {
            //currentNode的叔叔结点
            RedBlackNode uncle = (RedBlackNode) grandParent.right;
            //情况1 currentNode的父亲结点和叔叔结点都是红色
            //把它们两结点都变成黑色
            if (uncle.color == ColorEnum.RED) {
                //currentNode的父亲结点变成黑色
                parent.color = ColorEnum.BLACK;
                //currentNode的叔叔结点变成黑色
                uncle.color = ColorEnum.BLACK;
                //currentNode的爷爷结点变成红色
                grandParent.color = ColorEnum.RED;
                //如果grandparent被着色成红色，在接下来迭代中要检查它是否破坏了红黑树性质
                //currentNode指向grandparent，进一步检查
                currentNode = grandParent;
            }
            // 情况 2/3 currentNode的叔叔结点uncle是黑色 - 执行旋转操作
            else {
                if (currentNode == parent.right) { // 情况 2, 执行一次左旋，左旋currentNode
                    currentNode = parent;
                    rotateLeft(currentNode);
                }
                // do not use parent
                //currentNode的父亲结点涂黑
                parent.color = ColorEnum.BLACK; // 情况 3 currentNode是父亲结点的左孩子
                //currentNode的爷爷结点涂红
                grandParent.color = ColorEnum.RED;
                //执行一次右旋，右旋爷爷结点
                rotateRight(grandParent);
            }
        } else if (parent == grandParent.right) {
            //currentNode的叔叔结点
            RedBlackNode uncle = (RedBlackNode) grandParent.left;
            // 情况1 - currentNode的叔叔结点和父亲结点都是红色
            // 把它们重新着色成黑色
            if (uncle.color == ColorEnum.RED) {
                //currentNode的父亲结点涂黑
                parent.color = ColorEnum.BLACK;
                //currentNode的叔叔结点涂黑
                uncle.color = ColorEnum.BLACK;
                //currentNode的父亲结点的父亲结点涂红
                grandParent.color = ColorEnum.RED;
                //如果grandparent被着色成红色，在接下来迭代中要检查它是否破坏了红黑树性质
                //currentNode指向grandparent，进一步检查
                currentNode = grandParent;
            }
            // 情况 2/3 currentNode的叔叔结点是黑色 - 执行旋转操作
            else {
                if (currentNode == parent.left) { // 情况 2, 执行一次右旋，右旋currentNode
                    currentNode = parent;
                    rotateRight(currentNode);
                }
                // do not use parent
                //currentNode的父亲结点涂黑
                parent.color = ColorEnum.BLACK; // 情况 3 currentNode是父亲结点的右孩子
                //grandParent涂红
                grandParent.color = ColorEnum.RED;
                //执行一次左旋，左旋爷爷结点
                rotateLeft(grandParent);
            }
        }

    }
    //修复结束后确保根结点一定是黑色的
    ((RedBlackNode) root).color = ColorEnum.BLACK;
}

删除操作

TRANSPLANT

/**
 * 类似于BST原生的transplant()方法，但将null替换成哨兵结点
 * @param nodeToReplace 被取代的结点
 * @param newNode 新的结点
 * @return newNode取代nodeToReplace的位置
 */
private Node rbTreeTransplant(Node nodeToReplace, Node newNode) {
    if (nodeToReplace.parent == nilNode) {
        this.root = newNode;
    } else if (nodeToReplace == nodeToReplace.parent.left) {
        nodeToReplace.parent.left = newNode;
    } else {
        nodeToReplace.parent.right = newNode;
    }
    newNode.parent = nodeToReplace.parent;
    return newNode;
}

RBDELETE

记录removedOrMovedNode的踪迹，removedOrMovedNode可能导致红黑性质的破坏
当想要删除结点deleteNode，且
- 此时deleteNode的子结点少于两个时，deleteNode从树中删除，并让removedOrMovedNode成为deleteNode
- 当deleteNode有两个子结点时，removedOrMovedNode应该是deleteNode的后继，并且removedOrMovedNode将移至树中的deleteNode位置
当结点被移除或在树移动之前，必须记住removedOrMovedNode的颜色，并且记录replaceNode的踪迹，将replaceNode移至树中原来removedOrMovedNode的位置，因为结点replaceNode也可能引起红黑性质破坏
删除deleteNode后需要调整红黑树，保持性质

/**
 * 删除结点
 * Slightly modified delete routine for red-black tree.
 * @param deleteNode
 *           待删除的结点
 *
 * @return
 */
@Override
protected Node delete(Node deleteNode) {
    /*
        记录removedOrMovedNode的踪迹，removedOrMovedNode可能导致红黑性质的破坏

        当想要删除结点deleteNode，且
        1. 此时deleteNode的子结点少于两个时，deleteNode从树中删除，并让removedOrMovedNode成为deleteNode
        2. 当deleteNode有两个子结点时，removedOrMovedNode应该是deleteNode的后继，并且removedOrMovedNode将移至树中的deleteNode位置

        当结点被移除或在树移动之前，必须记住removedOrMovedNode的颜色，并且记录replaceNode的踪迹，
        将replaceNode移至树中原来removedOrMovedNode的位置，因为结点replaceNode也可能引起红黑性质破坏

        删除deleteNode后需要调整红黑树，保持性质
    * */

    //替换removedOrMovedNode的跟踪节点
    Node replaceNode = null; // track node that replaces removedOrMovedNode
    if (deleteNode != null && deleteNode != nilNode) {
        //如果deleteNode只有一个子节点，则与deleteNode相同，否则将替换deleteNode
        Node removedOrMovedNode = deleteNode; // same as deleteNode if it has only one child, and otherwise it replaces deleteNode
        ColorEnum removedOrMovedNodeColor = ((RedBlackNode)removedOrMovedNode).color;

        if (deleteNode.left == nilNode) { //当待删除结点的左孩子为空
            //replaceNode指向待删除结点的右孩子
            replaceNode = deleteNode.right;
            //用待删除结点的右孩子代替它
            rbTreeTransplant(deleteNode, deleteNode.right);
        } else if (deleteNode.right == nilNode) { //当待删除结点的右孩子为空
            //replaceNode指向待删除结点的左孩子
            replaceNode = deleteNode.left;
            //用待删除结点的左孩子代替它
            rbTreeTransplant(deleteNode, deleteNode.left);
        } else { //待删除结点的左右孩子都不空
            //removedOrMovedNode指向待删除孩子的后继（即其右孩子的最左边）
            removedOrMovedNode = getMinimum(deleteNode.right);
            //记住removedOrMovedNode的颜色
            removedOrMovedNodeColor = ((RedBlackNode)removedOrMovedNode).color;
            //replaceNode保存代替结点的右孩子
            replaceNode = removedOrMovedNode.right;
            //如果代替结点的直接父亲是待删除结点
            if (removedOrMovedNode.parent == deleteNode) {
                replaceNode.parent = removedOrMovedNode;
            } else { 如果代替结点的直接父亲不是待删除结点
                /*代替结点连接待删除结点的右孩子*/

                //代替结点的右孩子取代代替结点位置
                rbTreeTransplant(removedOrMovedNode, removedOrMovedNode.right);
                //代替结点的右孩子指针指向待删除结点的右孩子结点
                removedOrMovedNode.right = deleteNode.right;
                //待删除结点的右孩子的父亲指向代替结点
                removedOrMovedNode.right.parent = removedOrMovedNode;
            }

            //代替结点取代待删除结点的位置
            rbTreeTransplant(deleteNode, removedOrMovedNode);

            /*代替结点连接待删除结点的左孩子*/
            //代替结点的左指针指向待删除结点的左孩子
            removedOrMovedNode.left = deleteNode.left;
            removedOrMovedNode.left.parent = removedOrMovedNode;
            //代替结点的颜色和待删除结点颜色一致
            ((RedBlackNode)removedOrMovedNode).color = ((RedBlackNode)deleteNode).color;
        }

        size--;
        /*
            removedOrMovedNode是黑色，可能引入了一个或多个性质被破坏的情况
            1. removedOrMovedNode是红色，当removedOrMovedNodeColor被删除或者移动时，红黑性质仍保持
              （原因见 算法导论 第三版 第184页）
            2. removedOrMovedNode是黑色的
               a. 如果removedOrMovedNode是原来的根结点，而removedOrMovedNode的一个红色孩子成为新的根结点，违反性质2
               b. 如果replaceNode和replaceNode.parent是红色的，违反性质4
               c. 在树中移动removedOrMovedNode会导致先前包含removedOrMovedNode的任何简单路径上的黑结点数少1
        * */
        if (removedOrMovedNodeColor == ColorEnum.BLACK) {
            deleteRBFixup((RedBlackNode)replaceNode);
        }
    }
    return replaceNode;
}

DELETEFIXUP

假设顶替上来的结点是x，认为它有额外的一重黑色，这个黑色是从被删除结点继承来的
（如果删除一个结点后特性被破坏，那么被删除的结点一定是黑色，阐述红色结点不会破坏红黑树特性，因此继承来的颜色一定是黑色）
x有两种颜色，如果x原本是红色，现在的颜色便是红，黑
如果x原本是黑色，现在的颜色便是黑，黑
通过以上假设，黑色结点数目没有少，因为被删除的的结点的黑色被其他结点继承了

如何调整恢复红黑特性

x颜色为"红，黑"。直接删除其黑色保留黑色，所有特性即可恢复
x颜色为“黑，黑”，且x是根结点。无需调整（或者理解成无视其中一个黑色，将其视为普通的黑色结点即可）
x颜色是“黑，黑”且x不是根结点，分四种情况
- 情况1 x的兄弟结点是黑色，x的兄弟结点的两个孩子都是黑色
处理方法：将x的兄弟结点涂红。设置x的父结点为新的x结点，
1. 如果此时x是红色结点，则将其涂黑即可结束操作
2. 如果此时x是黑色结点，则x变成新的“黑，黑”结点，观察此时x的兄弟所对应的情形，继续进行处理，直到满足条件为止
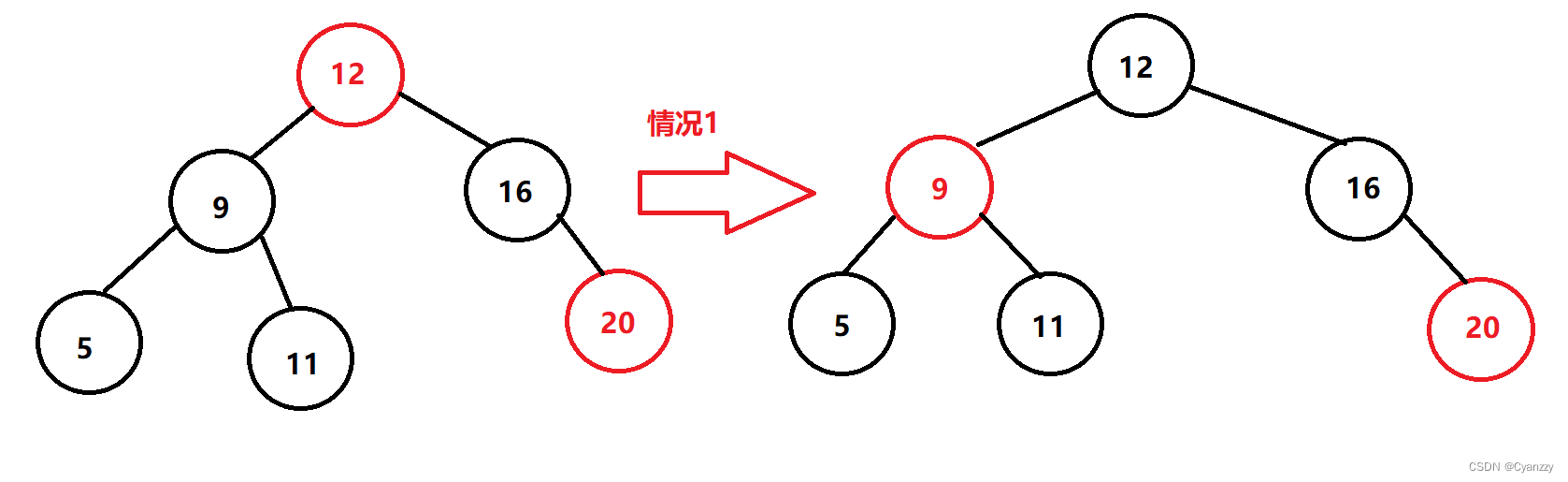
把兄弟节点涂红，让父节点成为新的当前节点，使使父节点为根的整个子树黑高度少1，违规位置上移。（蓝色代表任意颜色）
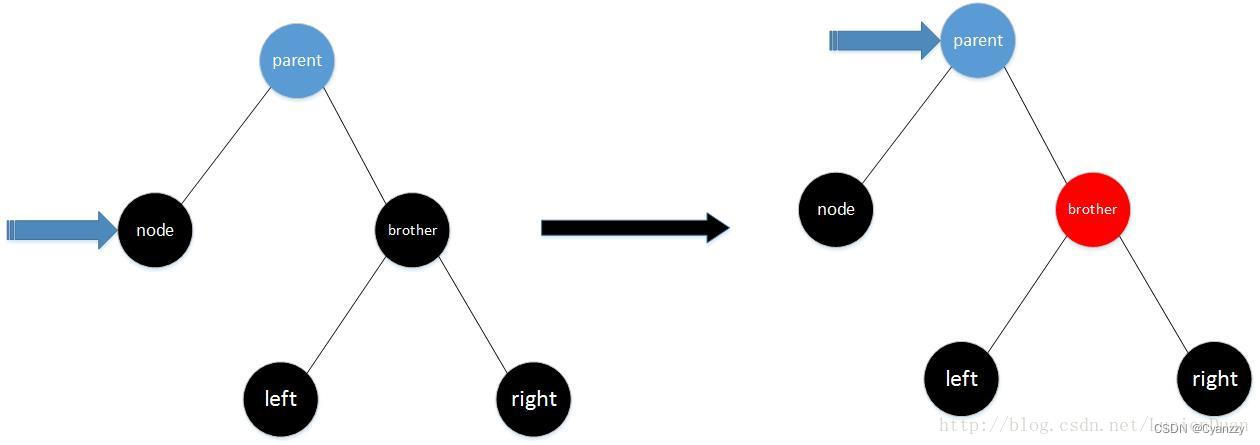
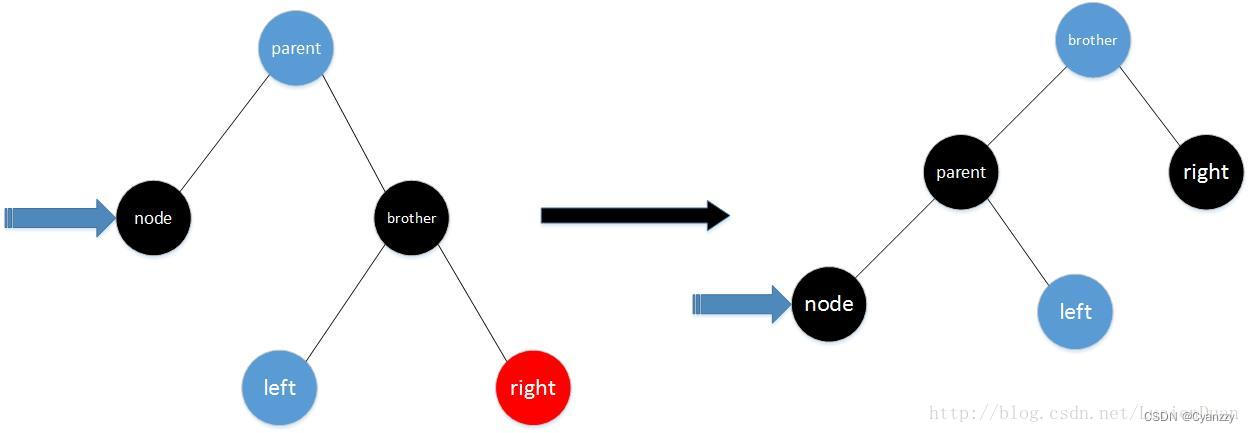
- 情况2 x的兄弟结点是红色
处理方法：
1. 将x的兄弟结点涂黑；将x的父结点涂为红色；对x的父结点进行旋转操作，x是左孩子则左旋转，x是右孩子则右旋转
2. 旋转后的x依然是“黑，黑”结点，观察此时x的兄弟结点所对应的情形，继续进行处理，直到满足结束条件为止
将这种情形转换成兄弟节点为黑的情形来处理，即：将当前节点的父节点涂红，兄弟节点涂黑，，以父节点为支点左旋，则当前节点的兄弟节点就为原来兄弟节点的左黑孩子，变成了兄弟节点为黑的情形。
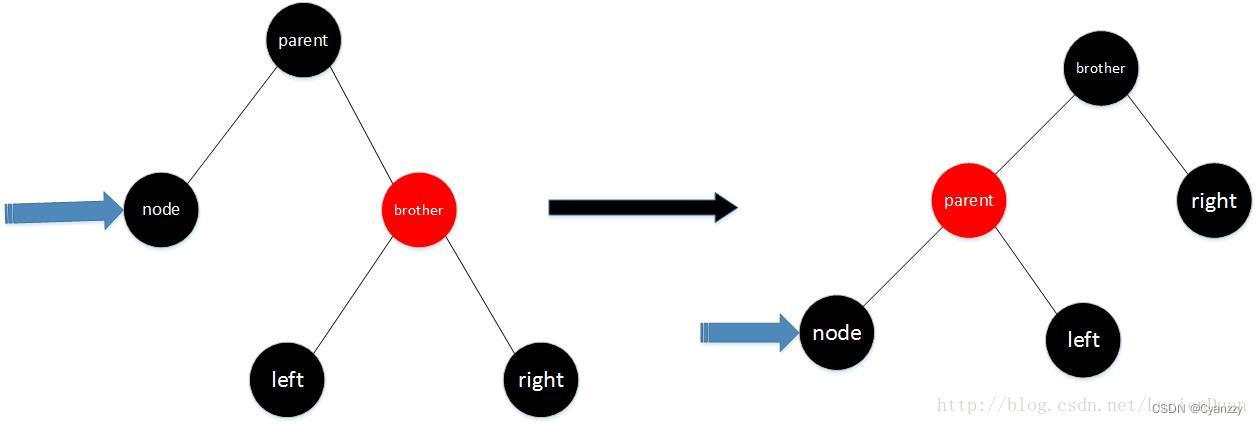
- 情况3 x的兄弟结点是黑色，x的兄弟结点左孩子是红色，右孩子是黑色
处理方法：
1. 将x兄弟结点的左孩子涂成黑色；将x的兄弟结点涂成红色
2. 对x的兄弟结点进行右旋，旋转后x依然是"黑，黑"结点，观察此时x的兄弟结点所对应的情形继续处理直到满足条件为止
将这种情形转换成兄弟节点的右孩子为红的情形来解决，即：将兄弟节点涂红，并将其左孩子涂黑，然后以兄弟节点为支点右旋，则当前节点的新的兄弟节点为原兄弟节点的左孩子，且想在兄弟节点的右孩子为红了。
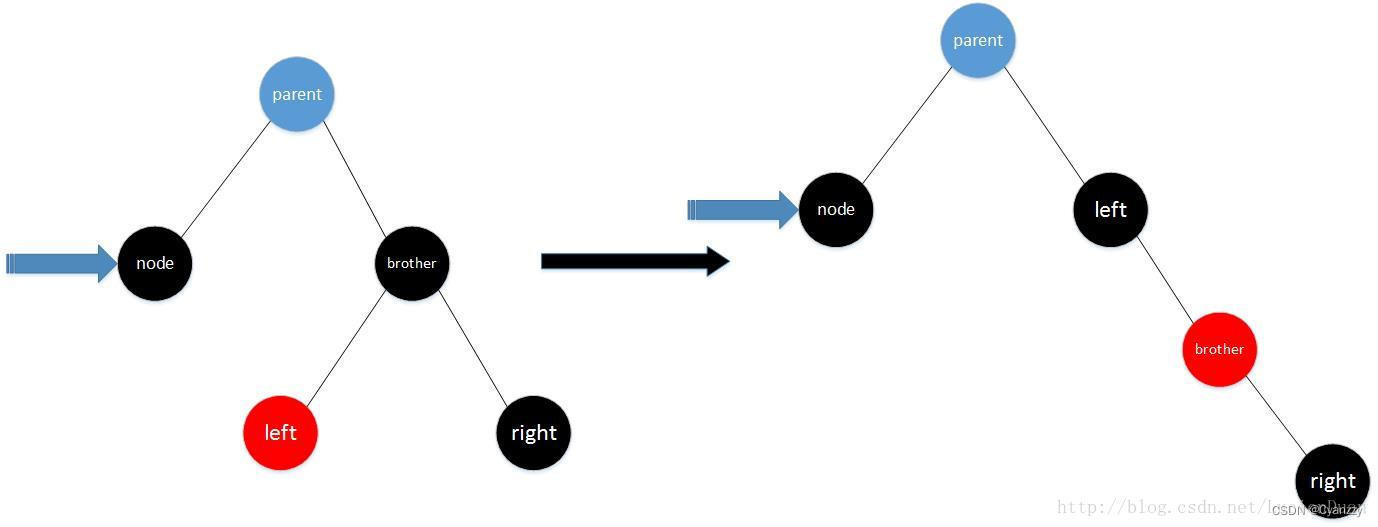
- 情况4 x的兄弟结点是黑色，x的兄弟结点右孩子是红色，左孩子颜色任意

处理方法：

将x父结点颜色赋值给x的兄弟结点
将x父结点颜色涂成黑色
将x兄弟结点的右孩子结点涂成黑色
对x的父结点进行旋转操作，x是左孩子则左旋转，x是右孩子则右旋转
旋转后x依然是“黑黑”结点，观察此时x的兄弟结点所对应的情况，继续进行处理，直到满足条件为止

可以先把兄弟节点涂成父节点的颜色，再把父节点和兄弟节点的右孩子涂黑，然后以父节点为支点左旋，此时所有性质都满足了

因为原本是当前节点的黑高度比兄弟节点少1，只与兄弟节点的孩子相同，经过这次变换，当前节点所在的位置变成了原来的黑父节点，黑高度增加了1，所以保持了性质5，而其它节点的黑高度也没有受到影响，依然没变。所以维护完成，算法结束。

在这里插入图片描述

CODE

@Override
protected Node delete(Node deleteNode) {
    /*
        记录removedOrMovedNode的踪迹，removedOrMovedNode可能导致红黑性质的破坏

        当想要删除结点deleteNode，且
        1. 此时deleteNode的子结点少于两个时，deleteNode从树中删除，并让removedOrMovedNode成为deleteNode
        2. 当deleteNode有两个子结点时，removedOrMovedNode应该是deleteNode的后继，并且removedOrMovedNode将移至树中的deleteNode位置

        当结点被移除或在树移动之前，必须记住removedOrMovedNode的颜色，并且记录replaceNode的踪迹，
        将replaceNode移至树中原来removedOrMovedNode的位置，因为结点replaceNode也可能引起红黑性质破坏

        删除deleteNode后需要调整红黑树，保持性质
    * */

    //替换removedOrMovedNode的跟踪节点
    Node replaceNode = null; // track node that replaces removedOrMovedNode
    if (deleteNode != null && deleteNode != nilNode) {
        //如果deleteNode只有一个子节点，则与deleteNode相同，否则将替换deleteNode
        Node removedOrMovedNode = deleteNode; // same as deleteNode if it has only one child, and otherwise it replaces deleteNode
        ColorEnum removedOrMovedNodeColor = ((RedBlackNode)removedOrMovedNode).color;

        if (deleteNode.left == nilNode) { //当待删除结点的左孩子为空
            //replaceNode指向待删除结点的右孩子
            replaceNode = deleteNode.right;
            //用待删除结点的右孩子代替它
            rbTreeTransplant(deleteNode, deleteNode.right);
        } else if (deleteNode.right == nilNode) { //当待删除结点的右孩子为空
            //replaceNode指向待删除结点的左孩子
            replaceNode = deleteNode.left;
            //用待删除结点的左孩子代替它
            rbTreeTransplant(deleteNode, deleteNode.left);
        } else { //待删除结点的左右孩子都不空
            //removedOrMovedNode指向待删除孩子的后继（即其右孩子的最左边）
            removedOrMovedNode = getMinimum(deleteNode.right);
            //记住removedOrMovedNode的颜色
            removedOrMovedNodeColor = ((RedBlackNode)removedOrMovedNode).color;
            //replaceNode保存代替结点的右孩子
            replaceNode = removedOrMovedNode.right;
            //如果代替结点的直接父亲是待删除结点
            if (removedOrMovedNode.parent == deleteNode) {
                replaceNode.parent = removedOrMovedNode;
            } else { 如果代替结点的直接父亲不是待删除结点
                /*代替结点连接待删除结点的右孩子*/

                //代替结点的右孩子取代代替结点位置
                rbTreeTransplant(removedOrMovedNode, removedOrMovedNode.right);
                //代替结点的右孩子指针指向待删除结点的右孩子结点
                removedOrMovedNode.right = deleteNode.right;
                //待删除结点的右孩子的父亲指向代替结点
                removedOrMovedNode.right.parent = removedOrMovedNode;
            }

            //代替结点取代待删除结点的位置
            rbTreeTransplant(deleteNode, removedOrMovedNode);

            /*代替结点连接待删除结点的左孩子*/
            //代替结点的左指针指向待删除结点的左孩子
            removedOrMovedNode.left = deleteNode.left;
            removedOrMovedNode.left.parent = removedOrMovedNode;
            //代替结点的颜色和待删除结点颜色一致
            ((RedBlackNode)removedOrMovedNode).color = ((RedBlackNode)deleteNode).color;
        }

        size--;
        /*
            removedOrMovedNode是黑色，可能引入了一个或多个性质被破坏的情况
            1. removedOrMovedNode是红色，当removedOrMovedNodeColor被删除或者移动时，红黑性质仍保持
              （原因见 算法导论 第三版 第184页）
            2. removedOrMovedNode是黑色的
               a. 如果removedOrMovedNode是原来的根结点，而removedOrMovedNode的一个红色孩子成为新的根结点，违反性质2
               b. 如果replaceNode和replaceNode.parent是红色的，违反性质4
               c. 在树中移动removedOrMovedNode会导致先前包含removedOrMovedNode的任何简单路径上的黑结点数少1
        * */
        if (removedOrMovedNodeColor == ColorEnum.BLACK) {
            deleteRBFixup((RedBlackNode)replaceNode);
        }
    }
    return replaceNode;
}

private void deleteRBFixup(RedBlackNode x) {
    /*
        while循环目标是将额外的黑色沿树上移，直到
        1. x指向红黑结点
        2. x指向根结点。此时简单移除额外的黑色
        3. 执行适当的旋转和重新着色，退出循环
    * */
    while (x != root && isBlack(x)) {

        //如果x是其父结点的左孩子
        if (x == x.parent.left) {
            //保持指针w指向x的兄弟
            RedBlackNode w = (RedBlackNode)x.parent.right;
            if (isRed(w)) { // case 1 - x的兄弟结点是红色
                //x的兄弟结点涂黑
                w.color = ColorEnum.BLACK;
                //x的父结点涂红
                ((RedBlackNode)x.parent).color = ColorEnum.RED;
                //对x的父结点旋转操作，当前x是父结点的左孩子，因此左旋
                rotateLeft(x.parent);
                w = (RedBlackNode)x.parent.right; // converted to case 2, 3 or 4
            }
            // case 2 x的兄弟结点是黑色，x的兄弟结点的两个孩子都是黑色
            if (isBlack(w.left) && isBlack(w.right)) {
                //将x的兄弟结点涂红
                w.color = ColorEnum.RED;
                //设置x的父结点为新的x结点
                x = (RedBlackNode)x.parent;
            } else if (w != nilNode) {
                if (isBlack(w.right)) { // case 3 x的兄弟结点是黑色，x的兄弟结点左孩子是红色，右孩子是黑色
                    //将x兄弟结点的左孩子涂黑
                    ((RedBlackNode)w.left).color = ColorEnum.BLACK;
                    //将x的兄弟结点涂红
                    w.color = ColorEnum.RED;
                    //对x兄弟结点右旋
                    rotateRight(w);
                    //w保持指向x的兄弟结点
                    w = (RedBlackNode)x.parent.right;
                }
                //将x父结点颜色设置给x兄弟结点
                w.color = ((RedBlackNode)x.parent).color; // case 4 x兄弟结点是黑色，x兄弟节点右孩子红色，左孩子颜色任意
                //将x父结点涂黑
                ((RedBlackNode)x.parent).color = ColorEnum.BLACK;
                //将x兄弟结点的右孩子设置黑色
                ((RedBlackNode)w.right).color = ColorEnum.BLACK;
                //对x的父结点旋转操作，x是左孩子，所以左旋转
                rotateLeft(x.parent);
                x = (RedBlackNode)root;
            } else {
                x.color = ColorEnum.BLACK;
                x = (RedBlackNode)x.parent;
            }
        } else {
            RedBlackNode w = (RedBlackNode)x.parent.left;
            if (isRed(w)) { // case 1 - sibling is red
                w.color = ColorEnum.BLACK;
                ((RedBlackNode)x.parent).color = ColorEnum.RED;
                rotateRight(x.parent);
                w = (RedBlackNode)x.parent.left; // converted to case 2, 3 or 4
            }
            // case 2 sibling is black and both of its children are black
            if (isBlack(w.left) && isBlack(w.right)) {
                w.color = ColorEnum.RED;
                x = (RedBlackNode)x.parent;
            } else if (w != nilNode) {
                if (isBlack(w.left)) { // case 3 sibling is black and its right child is red and left child is black
                    ((RedBlackNode)w.right).color = ColorEnum.BLACK;
                    w.color = ColorEnum.RED;
                    rotateLeft(w);
                    w = (RedBlackNode)x.parent.left;
                }
                w.color = ((RedBlackNode)x.parent).color; // case 4 sibling is black and left child is red
                ((RedBlackNode)x.parent).color = ColorEnum.BLACK;
                ((RedBlackNode)w.left).color = ColorEnum.BLACK;
                rotateRight(x.parent);
                x = (RedBlackNode)root;
            } else {
                x.color = ColorEnum.BLACK;
                x = (RedBlackNode)x.parent;
            }
        }

    }
}

跳表

增加了向前指针的链表叫作跳表。跳表全称叫做跳跃表，简称跳表。

跳表是一个随机化的数据结构，实质就是一种可以进行二分查找的有序链表。

跳表在原有的有序链表上面增加了多级索引，通过索引来实现快速查找。跳表不仅能提高搜索性能，同时也可以提高插入和删除操作的性能。

场景

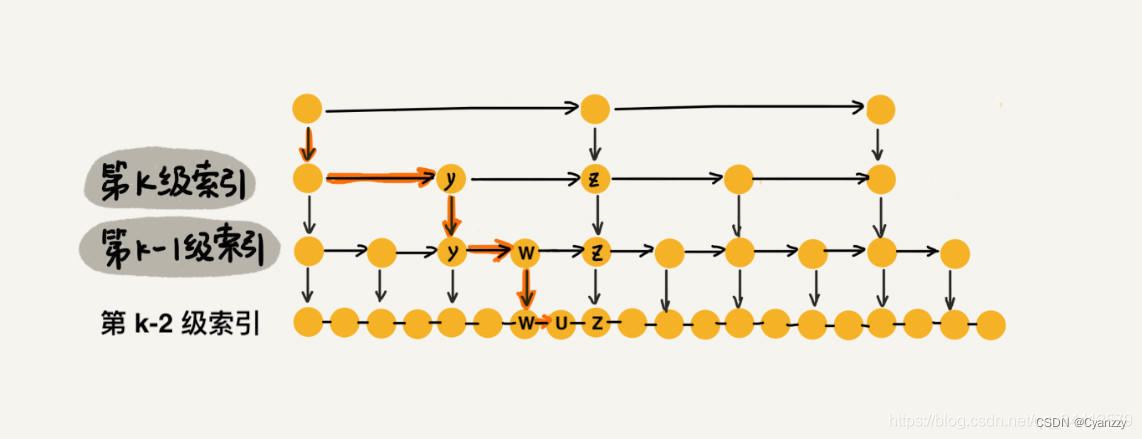
如下图所示，我们从链表中每两个元素抽出来，加一级索引，一级索引指向了原始链表

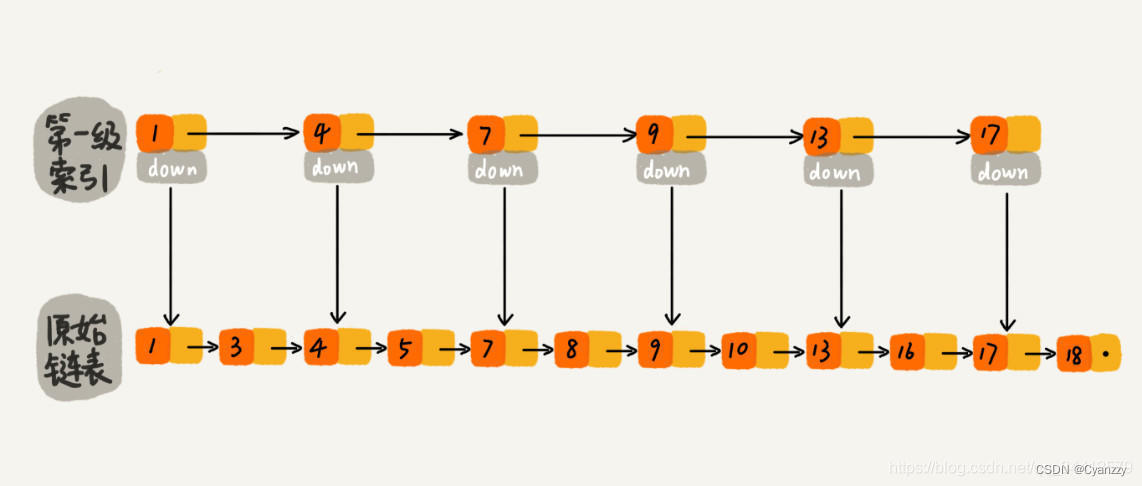
在这里插入图片描述

果加二级索引呢？如下图所示，查找路径：1、7、9、10。是不是找 10 的效率更高了？这就是跳表的思想，用“空间换时间”，通过给链表建立索引，提高了查找的效率。

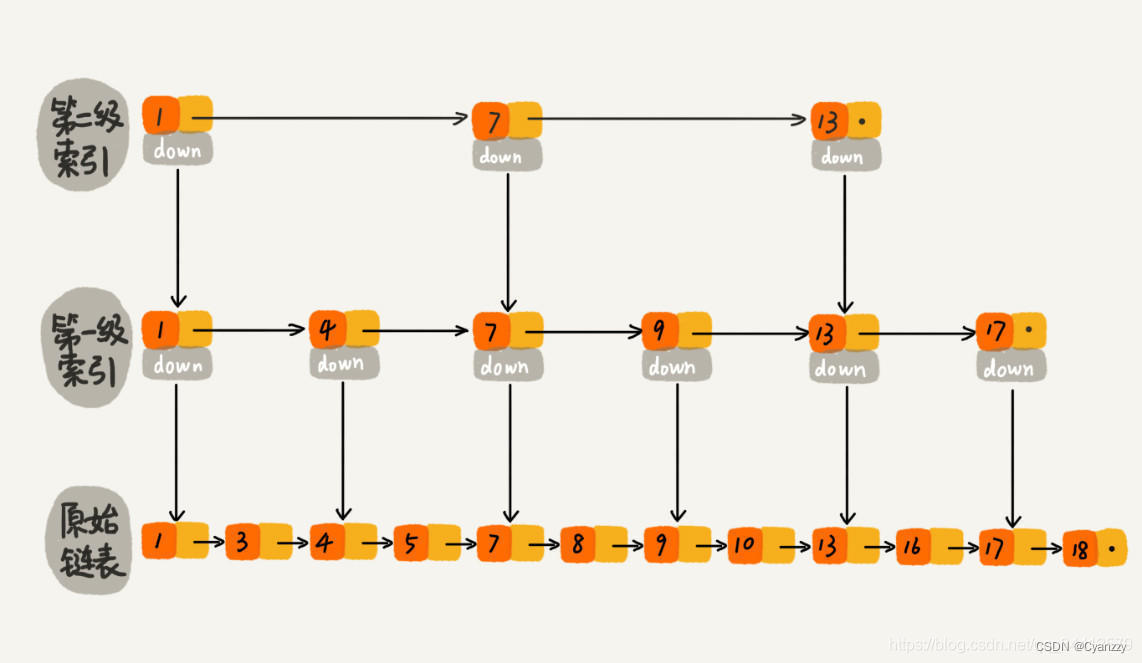
在这里插入图片描述

跳表是可以实现二分查找的有序链表。

查找操作

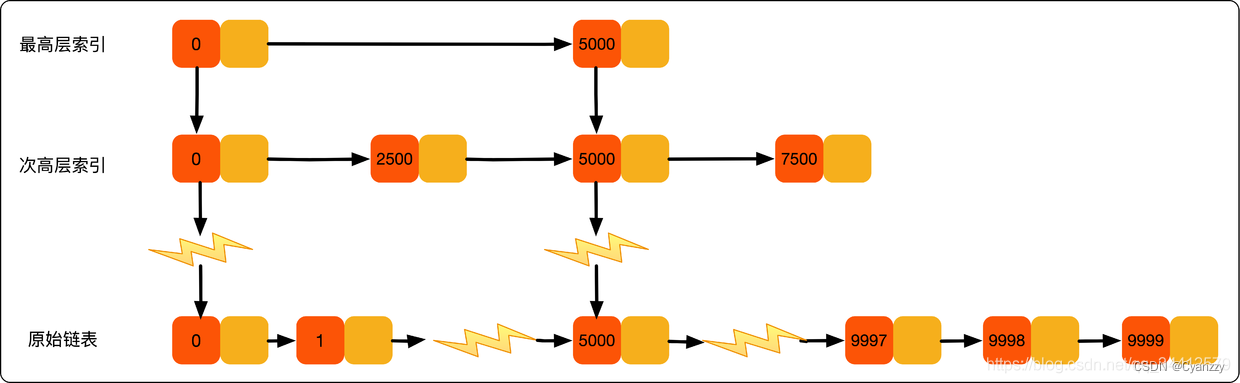
查找元素的过程是从最高级索引开始，一层一层遍历最后下沉到原始链表

时间复杂度

索引的高度 * 每层索引遍历元素的个数。

假设每两个结点会抽出一个结点作为上一级索引的结点，原始的链表有n个元素，则一级索引有n/2 个元素、二级索引有 n/4 个元素、k级索引就有 n/2^k个元素。最高级索引一般有2个元素，即：最高级索引 h 满足 2 = n/2^h，即 h = log2n - 1，最高级索引 h 为索引层的高度加上原始数据一层，跳表的总高度 h = log2n。
在这里插入图片描述
空间复杂度

假如原始链表包含 n 个元素，则一级索引元素个数为 n/2、二级索引元素个数为 n/4、三级索引元素个数为 n/8 以此类推。所以，索引节点的总和是：n/2 n/4 n/8 … 8 4 2 = n-2，空间复杂度是 O(n)。

插入操作

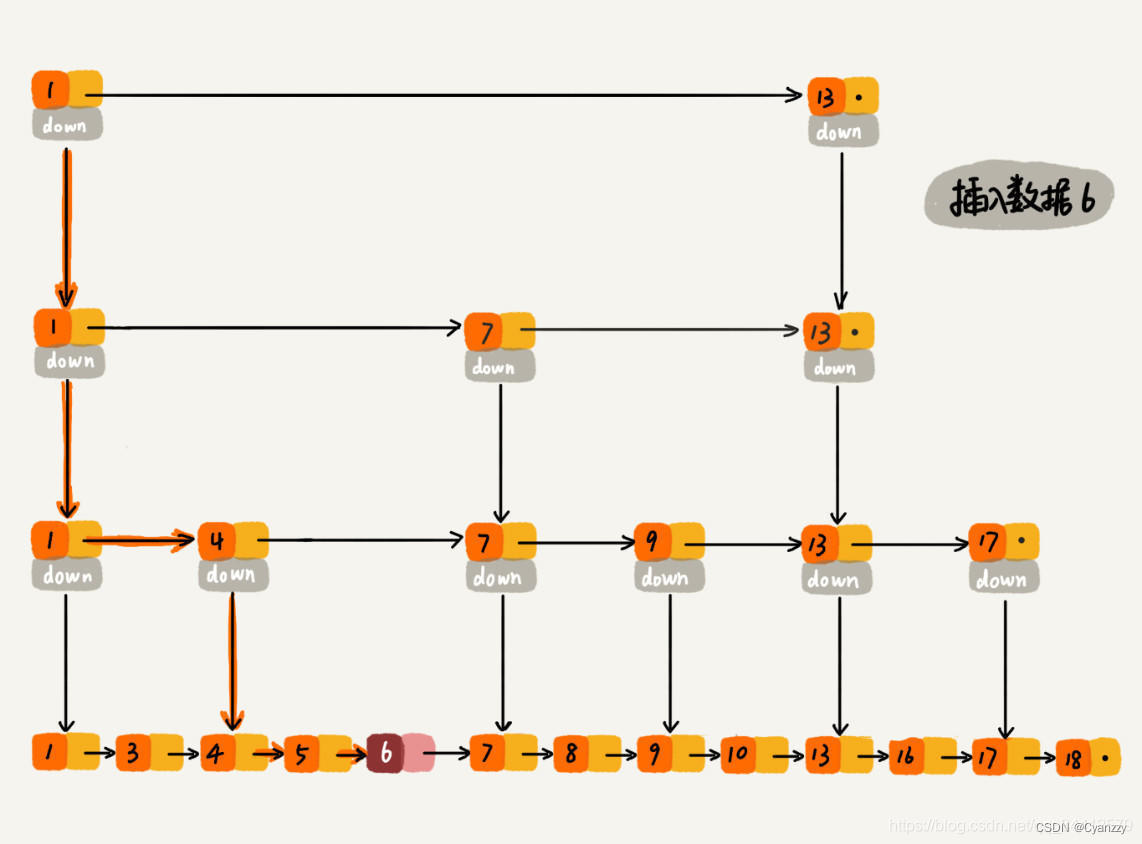
插入数据6，整个过程类似于查找6，整个的查找路径为 1、1、1、4、4、5。
查找到第底层原始链表的元素 5 时，发现 5 小于 6 但是后继节点 7 大于 6，所以应该把 6 插入到 5 之后 7 之前。
整个时间复杂度为查找元素的时间复杂度 $O (l o g n)$ 。

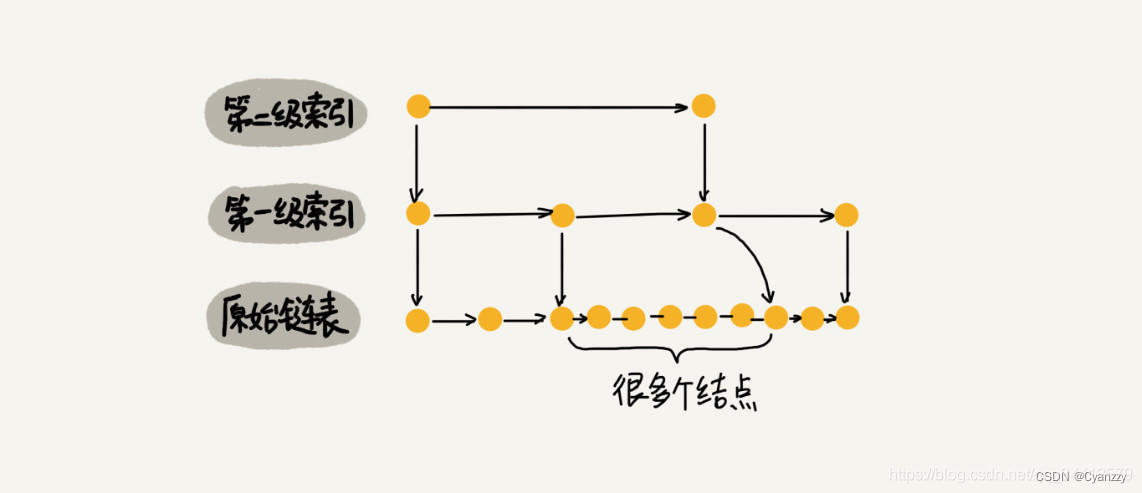
在这里插入图片描述

维护索引

在这里插入图片描述

当原始链表中元素数量足够大，且抽取足够随机的话，我们得到的索引是均匀的

可以维护一个这样的索引：随机选 n/2 个元素做为一级索引、随机选 n/4 个元素做为二级索引、随机选 n/8 个元素做为三级索引，依次类推，一直到最顶层索引

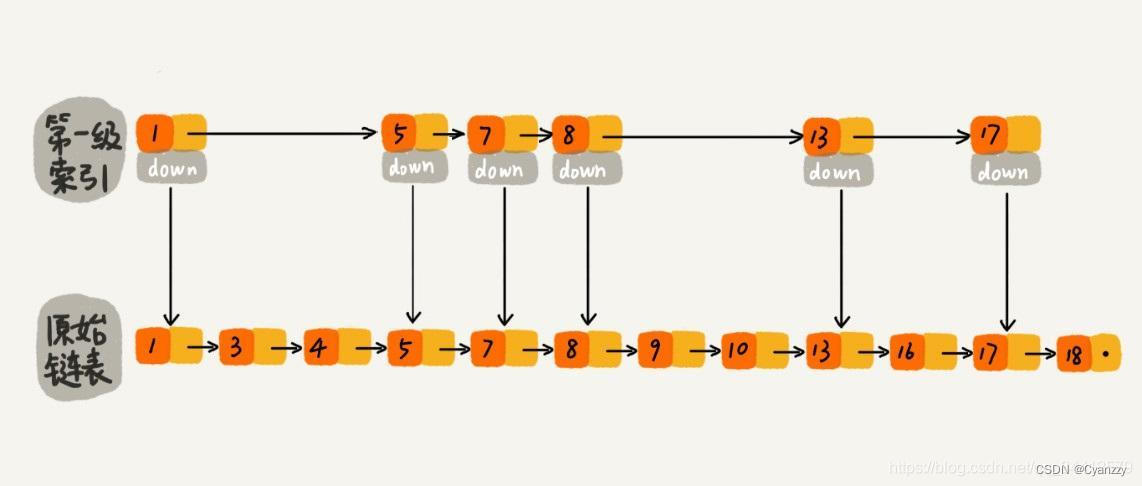
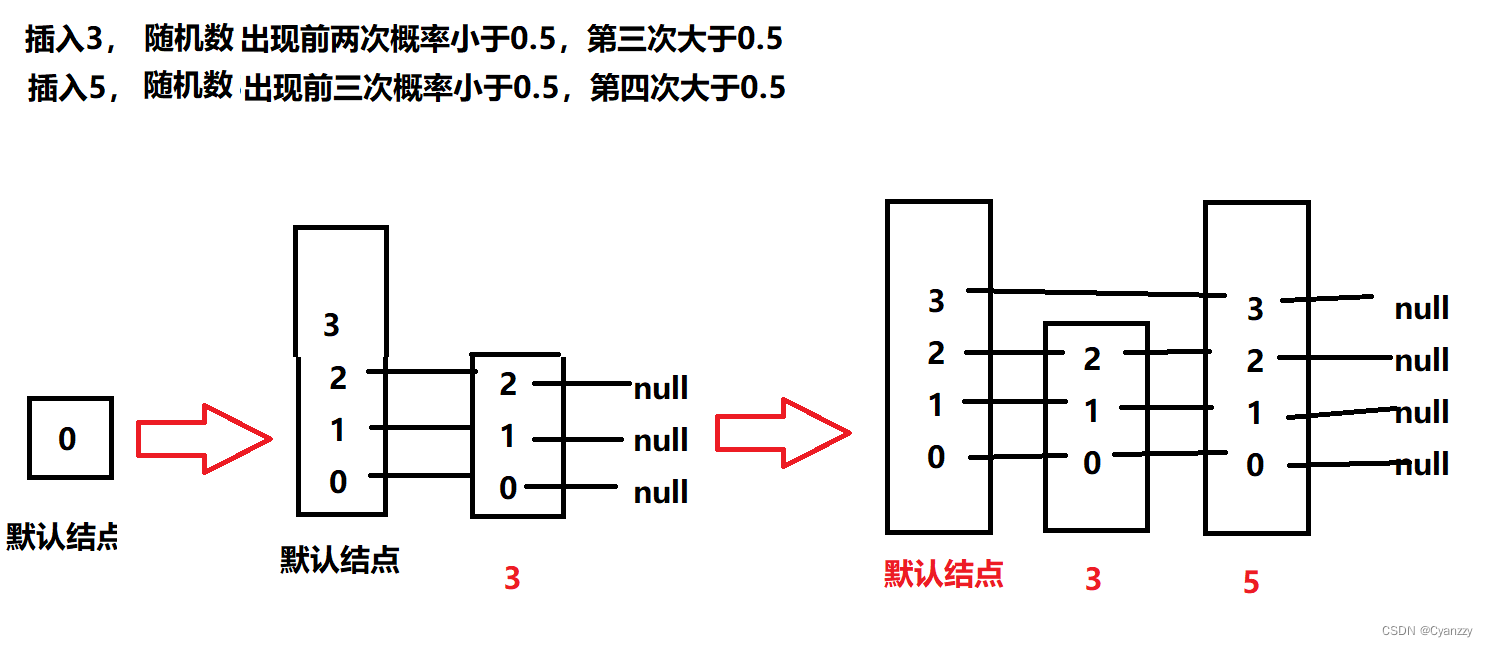
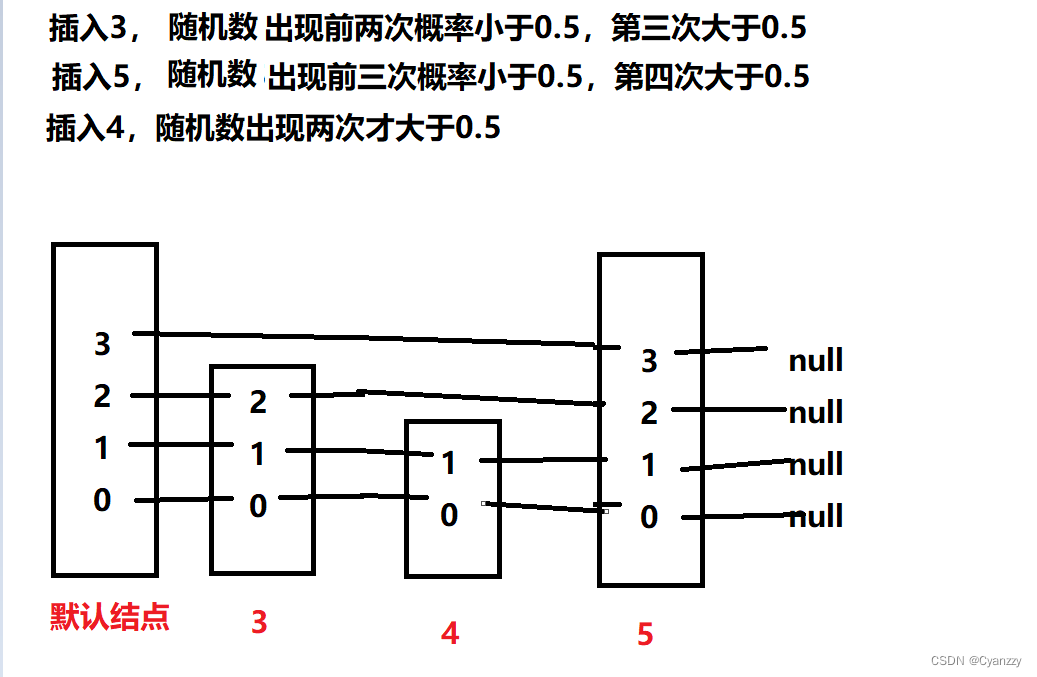
在这里插入图片描述

现在我们就需要一个概率算法帮我们把控这个 1/2、1/4、1/8 … ，当每次有数据要插入时，先通过概率算法告诉我们这个元素需要插入到几级索引中，然后开始维护索引并把数据插入到原始链表中

概率算法

该方法会随机生成 1~MAX_LEVEL 之间的数（MAX_LEVEL表示索引的最高层数），且该方法有 1/2 的概率返回 1、1/4 的概率返回 2、1/8的概率返回 3，以此类推。

randomLevel() 方法返回 1 表示当前插入的该元素不需要建索引，只需要存储数据到原始链表即可（概率 1/2）
randomLevel() 方法返回 2 表示当前插入的该元素需要建一级索引（概率 1/4）
randomLevel() 方法返回 3 表示当前插入的该元素需要建二级索引（概率 1/8）
randomLevel() 方法返回 4 表示当前插入的该元素需要建三级索引（概率 1/16）

在这里插入图片描述

public void put(K key, V value) {
    if (key == null) {
        return;
    }
    //找到小于key的最右边一个结点
    SkipListNode<K, V> less = mostRightLessNodeInTree(key);
    //当前数组中索引为0的结点
    SkipListNode<K, V> find = less.nextNodes.get(0);
    if (find != null && find.isKeyEqual(key)) {
        find.val = value;
    } else { //不是这个索引，新建结点
        size++;
        int newNodeLevel = 0;
        //计算新的索引级别
        while (Math.random() < PROBABILITY) {
            newNodeLevel++;
        }
        //更新索引级别
        while (newNodeLevel > maxLevel) {
            head.nextNodes.add(null);
            maxLevel++;
        }
        //新建结点
        SkipListNode<K, V> newNode = new SkipListNode<K, V>(key, value);
        //新结点的数组初始化next域
        for (int i = 0; i <= newNodeLevel; i++) {
            newNode.nextNodes.add(null);
        }
        int level = maxLevel;
        SkipListNode<K, V> pre = head;
        //从最高级别索引开始
        while (level >= 0) {
            //pre是当前索引级别level小于key的最右边结点
            pre = mostRightLessNodeInLevel(key, pre, level);
            if (level <= newNodeLevel) {
                //当前结点索引（级别）的next域更新成pre.next的值
                //类似链表的插入操作newNode.next=pr.next
                newNode.nextNodes.set(level, pre.nextNodes.get(level));
                //pre.next=newNOde
                pre.nextNodes.set(level, newNode);
            }
            //更新低级别的索引
            level--;
        }
    }
}

删除操作

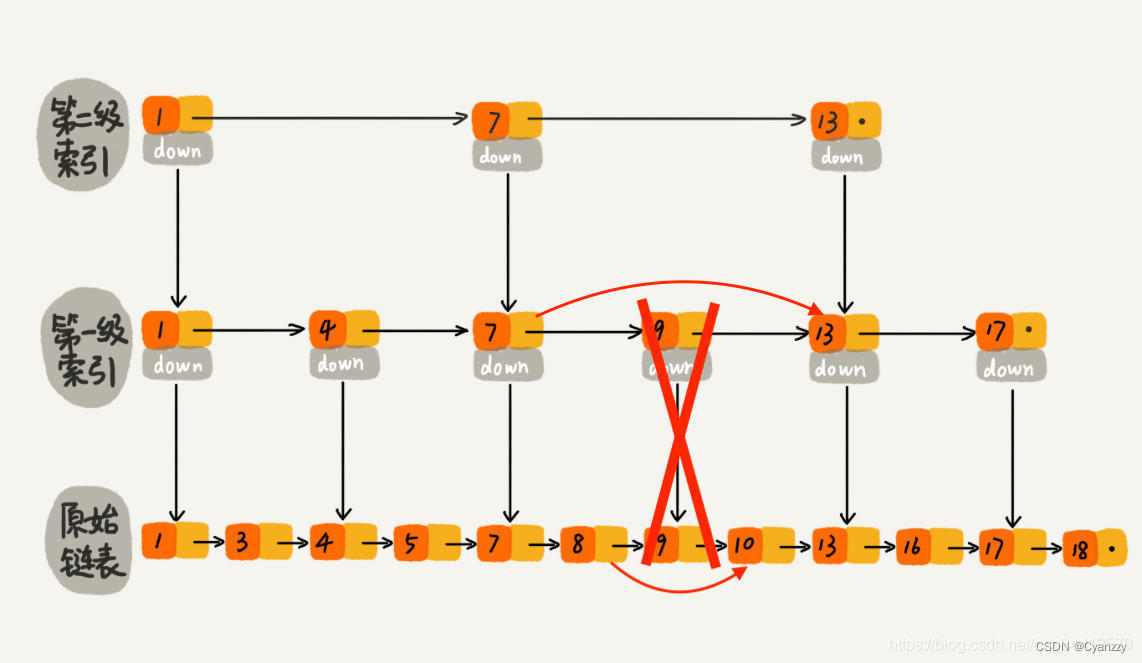
在这里插入图片描述

public void remove(K key) {
    if (containsKey(key)) {
        size--;
        int level = maxLevel;
        SkipListNode<K, V> pre = head;
        while (level >= 0) {
            //pre指向小于key的最右边一个结点
            pre = mostRightLessNodeInLevel(key, pre, level);
            //记住当前索引级别pre.next
            SkipListNode<K, V> next = pre.nextNodes.get(level);
            if (next != null && next.isKeyEqual(key)) {
                // free delete node memory -> C++
                //链表删除操作
                //pre.next = node.next
                pre.nextNodes.set(level, next.nextNodes.get(level));
            }
            //只有一个结点的删除情况
            if (level != 0 && pre == head && pre.nextNodes.get(level) == null) {
                head.nextNodes.remove(level);
                maxLevel--;
            }
            level--;
        }
    }
}