计算机中的 原码、反码、补码 详解
文章目录
- 1 概述
- 1.1 计算机存储单位
- 1.2 机器数和真值
- 1.3 数值
- 2 有符号数
- 2.1 原码
- 2.2 反码 和 补码
1 概述
1.1 计算机存储单位
| 大类 | 小类 | 解释 |
|---|---|---|
| 基本存储单位 | 位(bit) | 二进制数中的一个数位,0 和 1 组成,是计算机中数据的 最小单位 |
| 字节(Byte,B) | 1 字节 = 8 位,是计算机中数据的 基本单元。各种信息在计算机中存储 至少 需要一个字节 | |
| 扩展存储单位 | KB | 1 KB = 1024 B,基于字节换算而成,下同 |
| MB | 1 MB = 1024 KB | |
| GB | 1 GB = 1024 MB | |
| TB | 1 TB = 1024 GB |
在计算机内部,信息都是釆用 二进制(0 和 1) 的形式进行存储、运算、处理和传输的
1.2 机器数和真值
| 解释 | 举例 | |
|---|---|---|
| 机器数 | 一个数在计算机中的二进制表示形式 最高位为符号位:正数为 0,负数为 1 | 计算机存储 1 字节 = 8 位 ( + 3 ) 10 = 0 000 0011 , ( − 3 ) 10 = 1 000 0011 \begin{aligned}(+3)_{10} = \red 0000 \space\space 0011,(-3)_{10} = \red 1000 \space\space 0011\end{aligned} (+3)10=0000 0011,(−3)10=1000 0011 |
| 真值 | 机器数对应的真正数值 | 0000 0011 的真值 = +000 0011 = +3,1000 0011 的真值 = -000 0011 = -3 |
提醒:因为第一位是符号位,所以机器数的形式值就不等于真正的数值
例如:上面的有符号数 1000 0011,其最高位 1 代表负,其真正数值是 -3,而不是形式值 131, ( 10000011 ) 10 = 131 \begin{aligned}(1000 0011)_{10} = 131\end{aligned} (10000011)10=131
1.3 数值
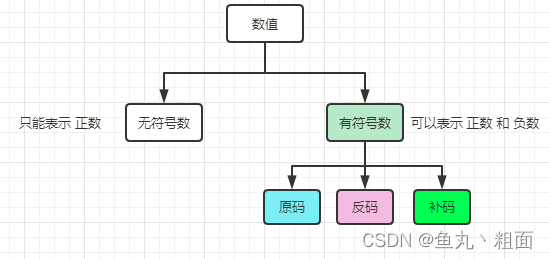
2 有符号数
| 带符号数 | 解释 | 计算规则 | 举例 |
|---|---|---|---|
| 原码 | 第一位表示符号,其余位表示值 | [+1] = [0000 0001]原 [-1] = [ 1000 0001]原 | |
| 反码 | 中间过渡码,可通过反码求补码 | 正数:等于 原码 负数:在原码的基础上,符号位不变,其余按位取反 | [+1] = [0000 0001]原 = [0000 0001]反[-1] = [ 1000 0001]原 = [1111 1110]反 |
| 补码 | 解决数值计算中的减法问题 | 正数:等于 原码 负数:在反码的基础上 + 1 | [+1] = [0000 0001]原 = [0000 0001]补[-1] = [ 1000 0001]原 = [1111 1111]补 |
2.1 原码
- 原码:符号位 加上 真值 的绝对值,即:用第一位表示符号,其余位表示值
- 比如:[+1]原= 0000 0001,[-1]原= 1000 0001
- 取值范围:除第一位符号位外,还余 7 位
- [1111 1111 , 0111 1111] = [ − ( 2 7 − 1 ) -(2^7-1) −(27−1), ( 2 7 − 1 ) (2^7-1) (27−1)] = [-127 , 127]
- 特点:人脑最容易理解和计算的表示方式(机器数:计算机最容易理解)
2.2 反码 和 补码
思考:既然原码才是被人脑直接识别并用于计算表示方式,为何还会有反码和补码呢?
- 首先,因为人脑可以知道第一位是 符号位,在计算的时候会根据符号位,选择对 真值 区域进行加减。但是对于计算机,加减已经是最基础的运算,而辨别符号位会让计算机的基础电路设计变得十分复杂。
- 于是,人们想出了将符号位也参与运算的方法。根据运算法则可知:减去一个正数等于加上一个负数,即:1-1 = 1 + (-1) = 0, 所以机器可以只有加法而没有减法,这样计算机运算的设计就更简单了。
- 于是,人们开始探索将符号位参与运算,并且只保留加法的方法。
以下为 '原码、反码、补码' 运算时的区别
对于十进制的表达式:1 - 1 = 0
1. 对于 '原码':
1 - 1
= 1 + (-1)
= [0000 0001]原 + [1000 0001]原
= [1000 0010]原
= -2
显然对于减法来说,结果是不正确的。这也就是为何计算机内部不使用原码表示一个数。
* 为了解决 '原码' 做减法的问题, 出现了 '反码':
2. 对于 '反码'
1 - 1
= 1 + (-1)
= [0000 0001]原 + [1000 0001]原
= [0000 0001]反 + [1111 1110]反
= [1111 1111]反
= [1000 0000]原
= -0
发现用反码计算减法,结果的真值部分是正确的。
而唯一的问题就出现在 "0" 这个特殊的数值上,虽然人们理解上 +0 和 -0 是一样的,
但是 0 带符号是没有任何意义的,而且会有[0000 0000]原和[1000 0000]原两个编码表示0
* 为了解决 0 的符号以及两个编码问题,出现了 '补码'
3. 对于 '补码'
1 - 1
= 1 + (-1)
= [0000 0001]原 + [1000 0001]原
= [0000 0001]补 + [1111 1111]补
= [1 0000 0000]补 -- 注意:进位 1 不在计算机字长里
= [0000 0000]补
= [0000 0000]原
= 0
这样 0 用 [0000 0000] 表示,而以前出现问题的 -0 则不存在了。
而且可以用 [1000 0000] 表示 -128:-128的由来如下:
(-1) + (-127)
= [1000 0001]原 + [1111 1111]原
= [1111 1111]补 + [1000 0001]补
= [1000 0000]补
= -128
请注意:-128 没有 原码 和 反码表示方式(以前用 -0 表示 -128)
使用补码,不仅仅修复了0的符号以及存在两个编码的问题,而且还能够多表示一个最低数。
这就是为什么8位二进制,使用原码或反码表示的范围为[-127, +127],
而使用补码表示的范围为[-128, 127]。
