一和零

动态规划（01背包，三级数组）

和经典的背包问题只有一种容量不同，这道题有两种容量，即选取的字符串子集中的 0 和 1 的数量上限。

经典的背包问题可以使用二维动态规划求解，两个维度分别是物品和容量。这道题有两种容量，因此需要使用三维动态规划求解，三个维度分别是字符串、0的容量和 1 的容量。

定义三维数组dp，其中dp[i][j][k] 表示在前 i 个字符串中，使用 j 个 0 和 k 个 1 的情况下最多可以得到的字符串数量。

当 0 和 1 的容量分别是 j 和 k 时，考虑以下两种情况：

• 如果 j< zeros 或 k<ones，则不能选第 i 个字符串，此时有 dp[i][j][k] = dp[i−1][j][k]；

• 如果 j ≥ zeros 且 k ≥ones，则如果不选第 i个字符串，有dp[i][j][k]=dp[i−1][j][k]，如果选第 i个字符串，有 dp[i][j][k]=dp[i−1][j−zeros][k−ones]+1，dp[i][j][k] 的值应取上面两项中的最大值。

因此状态转移方程如下：

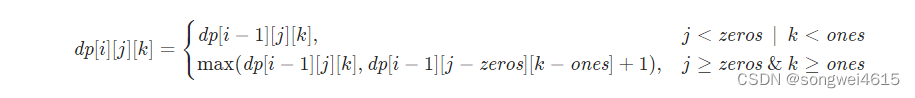
class Solution {
public:
    int find_0(string s1)
    {
        int num = 0;
        for(auto it:s1) if(it == '0') num++;
        return num;
    }

    int findMaxForm(vector<string>& strs, int m, int n) {

        vector<vector<vector<int>>>  dp( strs.size() ,vector<vector<int>>( m+1 ,vector<int>( n+1,0) ));
        int num_0 = 0,num_1 = 0;
        num_0 = find_0(strs[0]);
        num_1 = strs[0].size() - num_0;
        for(int j=0 ; j<= m ;j++)
        {
            for(int k=0 ; k<= n ;k++)
            {
               
                if( j>= num_0 && k>= num_1)
                    dp[0][j][k] = 1;
            }
           
        }

        
        for(int i=1 ; i<strs.size() ; i++)
        {
            num_0 = find_0(strs[i]);
            num_1 = strs[i].size() - num_0;
            for(int j=0 ; j<=m ;j++)
            { 
                for(int k=0 ; k<=n ;k++)
                {
                    
                     if( j>= num_0 && k>= num_1)
                        dp[i][j][k] = max( dp[i-1][j][k], dp[i-1][j - num_0][k - num_1] + 1);
                     else
                        dp[i][j][k] = dp[i-1][j][k];
                }
            }
        }
        
        int max_num = 0;
        for(int i=0 ; i<strs.size() ; i++)
        {
            if(dp[i][m][n] > max_num) max_num = dp[i][m][n];
            // cout<<dp[i][m][n]<<' ';
        }
            
        return max_num ;
    }
};

动态规划（滑动数组，二级数组）

由于dp[i][][] 的每个元素值的计算只和dp[i−1][][] 的元素值有关，因此可以使用滚动数组的方式，去掉 dp 的第一个维度，将空间复杂度优化到 O(mn)O(mn)。

实现时，内层循环需采用倒序遍历的方式，这种方式保证转移来的是 dp[i−1][][] 中的元素值。

class Solution {
public:
    int find_0(string s1)
    {
        int num = 0;
        for(auto it:s1) if(it == '0') num++;
        return num;
    }

    int findMaxForm(vector<string>& strs, int m, int n) {

        vector<vector<int>>  dp( m+1 ,vector<int>(n+1,0));

        int num_0 = 0,num_1 = 0;
        for(int i=0 ; i<strs.size() ; i++)
        {
            num_0 = find_0(strs[i]);
            num_1 = strs[i].size() - num_0;
            for(int j=m ; j>=num_0;j--)
            { 
                for(int k=n ; k>=num_1 ;k--)
                {
                    dp[j][k] = max( dp[j][k], dp[j - num_0][k - num_1] + 1);
                }
            }
        }
        return dp[m][n] ;
    }
};