java优先级队列(堆)

文章目录
- 一、优先级队列是什么?
- 二、堆
- 什么是堆?
- 堆的分类:
- 堆的存储
- 堆的创建
- 三、堆的操作
- 插入元素
- 弹出元素
- 四、用堆模拟实现优先级队列
一、优先级队列是什么?
在数据结构中,普通的队列是先进先出,但有时我们可能并不想有这么固定的规矩,我们希望能有一个带优先级的队列。考虑在现实生活中,一些服务排队窗口会写着“军人依法优先”;送进医院的患者,即便是按顺序到达的,生病更加严重的往往优先级也会更高;还有操作系统中的作业调度也和优先级有关…
于是我们能不能改进队列?使得队列是有一定优先级的,这样能让一些事物和任务的处理变的更加灵活。当然是可以的,最基本的我们可以基于线性结构来实现,考虑基于线性结构的时间复杂度:
1、队列是一种FIFO(First-In-First-Out)先进先出的数据结构,对应于生活中的排队的场景,排在前面的人总是先通过,依次进行。
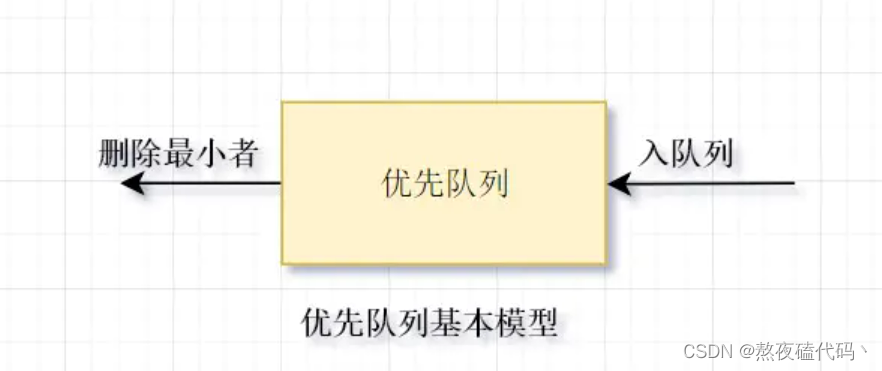
2、优先队列是特殊的队列,从“优先”一词,可看出有“插队现象”。比如在火车站排队进站时,就会有些比较急的人来插队,他们就在前面先通过验票。优先队列至少含有两种操作的数据结构:insert(插入),即将元素插入到优先队列中(入队);以及deleteMin(删除最小者),它的作用是找出、删除优先队列中的最小的元素(出队)。
二、堆
什么是堆?
堆严格意义上来说又叫二叉堆(Binary Heap),因为它的结构是一颗完全二叉树,堆一般分为最大堆和最小堆。
堆性质:
结构性:堆是一颗除底层外被完全填满的二叉树,底层的节点从左到右填入,这样的树叫做完全二叉树。即缺失结点的部分一定再树的右下侧。
堆序性:由于我们想很快找出最小元,则最小元应该在根上,任意节点都小于它的后裔,这就是小顶堆(Min-Heap);如果是查找最大元,则最大元应该在根上,任意节点都要大于它的后裔,这就是大顶堆(Max-heap)。
堆的分类:
最大堆:父亲节点的值大于孩子节点的值
最小堆:父亲节点的值小于孩子节点的值
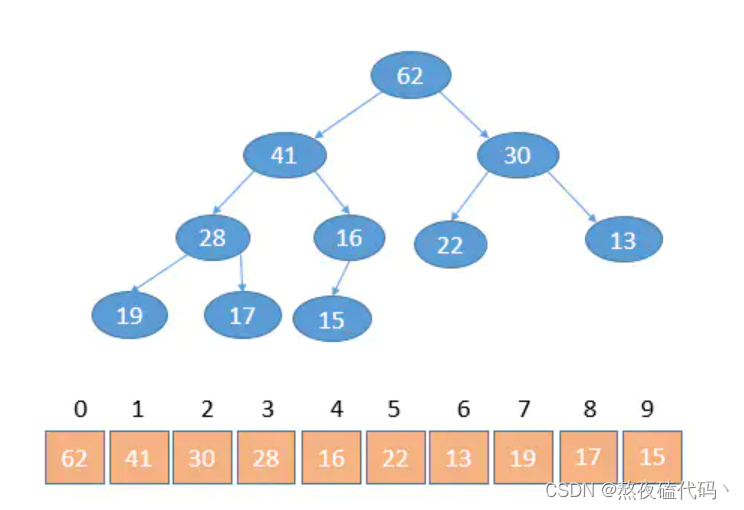
将元素存储到数组中后,可以根据二叉树的性质对树进行还原。假设i为节点在数组中的下标,则有:
如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2
如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子
如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子
堆的存储
从堆的概念可知,堆是一棵完全二叉树,因此可以层序的规则采用顺序的方式来高效存储
注意:对于非完全二叉树,则不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空节
点,就会导致空间利用率比较低。
堆的创建
我们创建堆是思路是:向下操作。
- 让parent标记需要调整的节点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子)
- 如果parent的左孩子存在,即:child < size, 进行以下操作,直到parent的左孩子不存在
parent右孩子是否存在,存在找到左右孩子中最小的孩子,让child进行标
将parent与较小的孩子child比较,如果:
parent小于较小的孩子child,调整结束
否则:交换parent与较小的孩子child,交换完成之后,parent中大的元素向下移动,可能导致子
树不满足对的性质,因此需要继续向下调整,即parent = child;child = parent*2+1; 然后继续2。
public int[] elem;
public int usedSize;
public static final int DEFAULT_SIZE = 10;
public priorityQueue() {
this.elem = new int[DEFAULT_SIZE];
}
/**
* 建堆的时间复杂度为O(n)
* 不能只看代码去猜测
*/
public void createHeap(int[] array) {
//检查数组容量,不够就进行扩容
if(elem.length < array.length) {
elem = Arrays.copyOf(elem, array.length * 2);
}
for (int i = 0; i < array.length; i++) {
elem[i] = array[i];
usedSize++;
}
for (int i = (usedSize - 1 - 1) / 2; i >= 0; i--) {
shiftDown(i,usedSize - 1);
}
}
/**
* 调整每颗子树的时间复杂度为O(log n)
* root为每棵子树的根节点
* len为每棵子树的结束条件
* @return
*/
private void shiftDown(int root,int len) {
int child = root * 2 + 1;
while(child <= len) {
if(child + 1 < len && elem[child + 1] > elem[child]) {
child++;
}
if(elem[root] >= elem[child]) {
return;
} else {
int h = elem[root];
elem[root] = elem[child];
elem[child] = h;
root = child;
child = root * 2 + 1;
}
}
}
三、堆的操作
插入元素
/**
* 入队之后要保证仍然为大根堆
* 所以我们插入到最后位置,然后向上调整
* @param val
*/
public void push(int val) {
//检查堆是否满了,满了进行扩容
if(isFull()) {
elem = Arrays.copyOf(elem,elem.length * 2);
}
elem[usedSize] = val;
usedSize++;
shiftUp(usedSize - 1);
}
private void shiftUp(int child) {
int parent = (child - 1) / 2;
while(child > 0) {
if(elem[parent] >= elem[child]) {
return;
}
int h = elem[child];
elem[child] = elem[parent];
elem[parent] = h;
child = parent;
parent = (child - 1) / 2;
}
}
当我们要在堆中插入元素时,因为插入元素后仍然要保证二叉树是一个大堆,所以我们选择把元素插在末尾位置,先判断堆是否为满,如果为满先扩容。
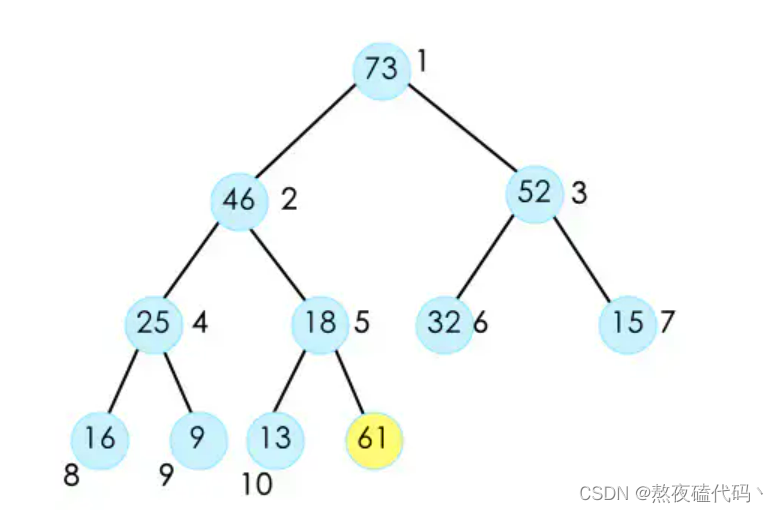
用该位置元素和父亲元素比较,如果大于父亲元素,则交换父子元素,然后指向父亲的位置。
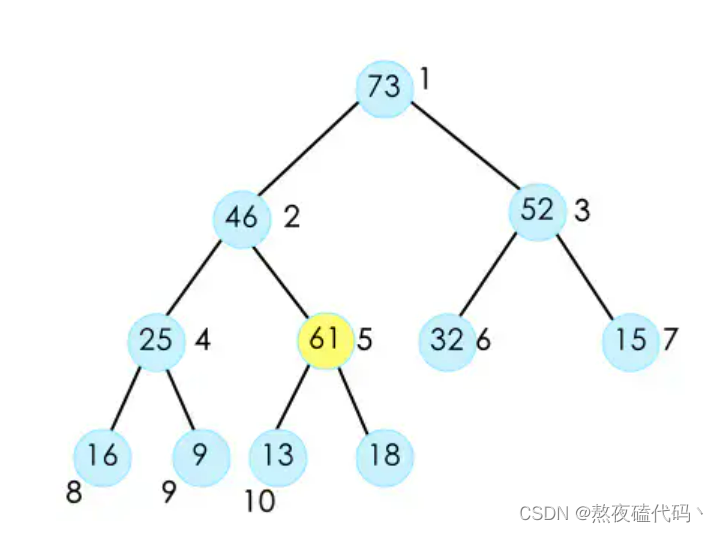
在与该位置的父亲位置元素比较,如果父亲元素大则重复上述操作,否则插入结束。
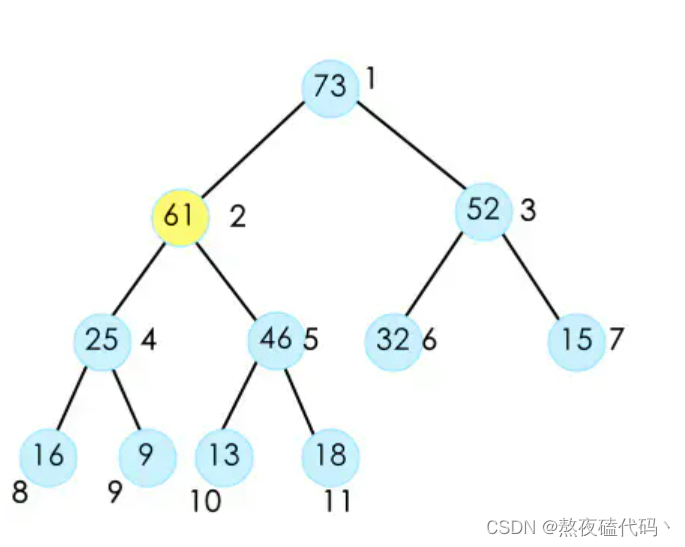
弹出元素
public void pollHeap() {
//判断堆是否为空
if(isEmpty()) {
return;
}
int h = elem[0];
elem[0] = elem[usedSize - 1];
elem[usedSize - 1] = h;
usedSize--;
shiftDown(0,usedSize - 1);
}
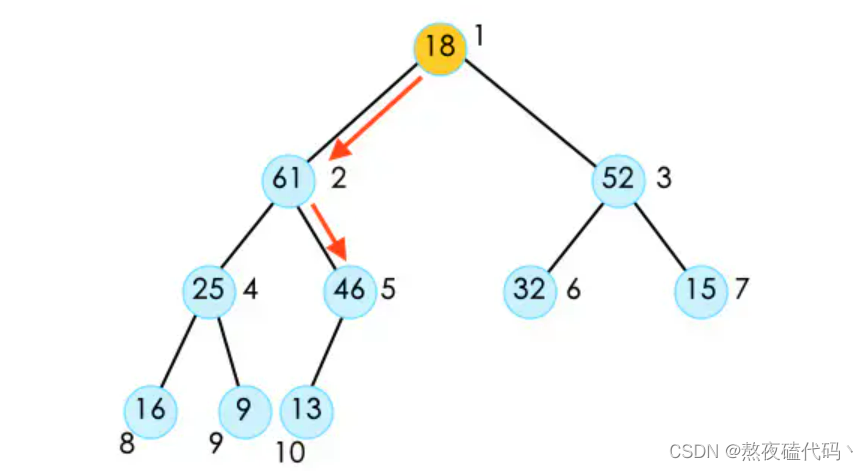
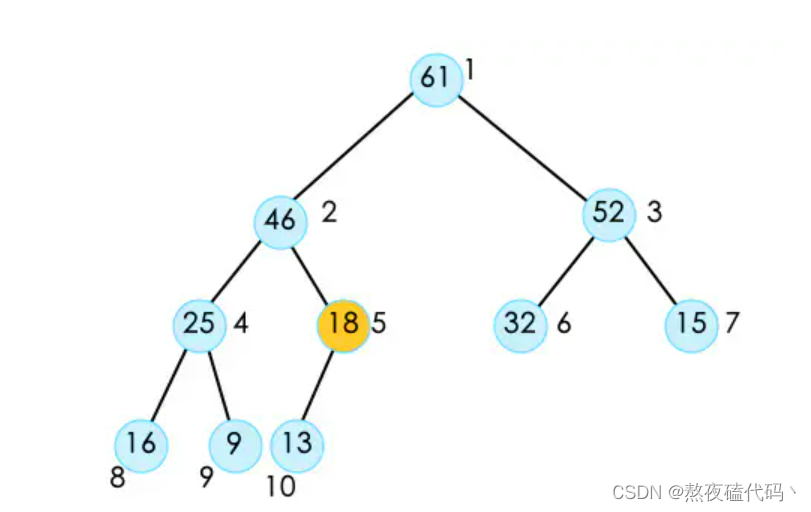
弹出元素和删除堆首元素的思路大致相同。时间复杂度为O(logn)
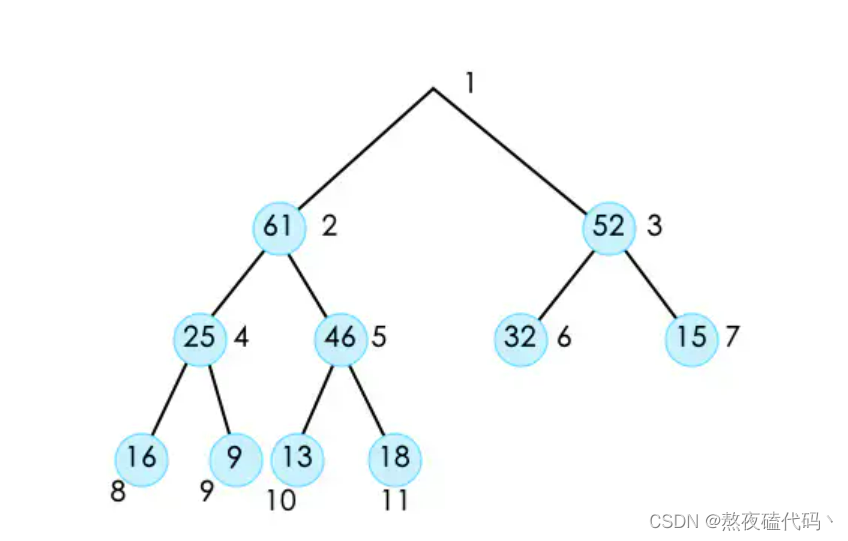
先将堆尾元素和堆首元素进行交换,然后将usedSize–.
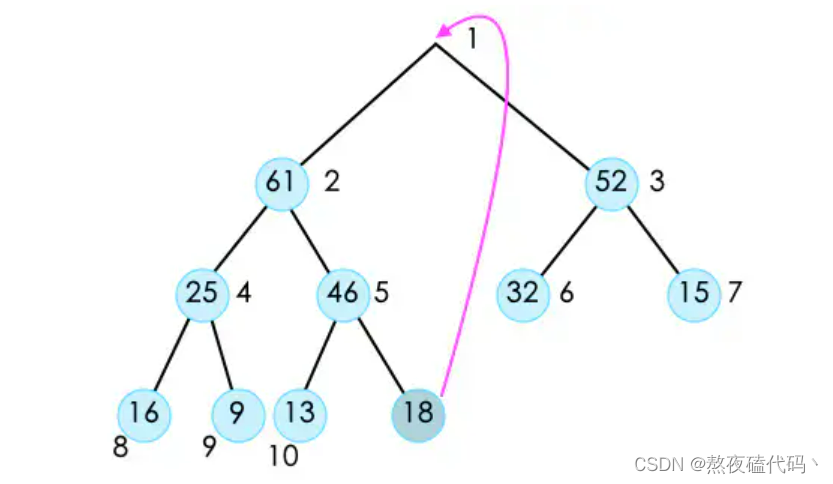
接下来只需要对堆首元素向下操作即可。
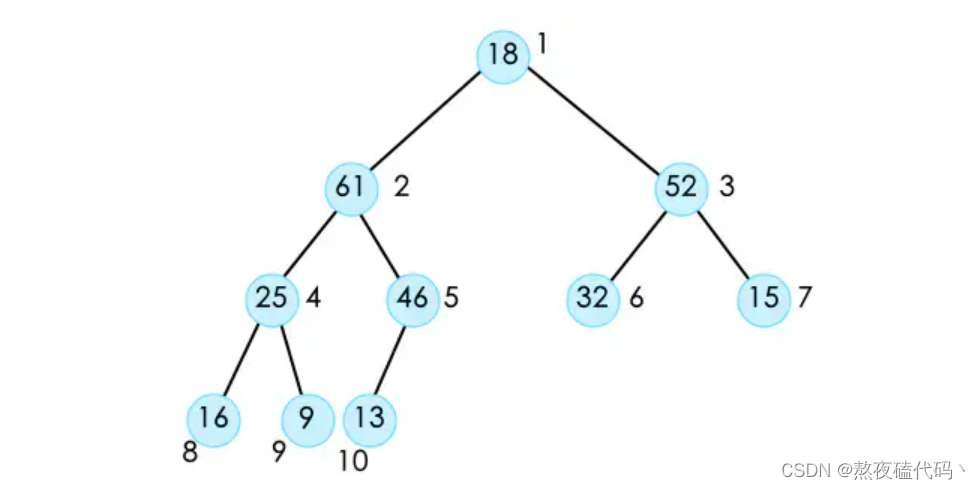
此时这个堆已经不符合最大堆的性质。为了保持这个性质,我们需要将堆顶的元素调整到它应该在的位置。也就是对它进行shift Down操作。在shift down时,因为它有左右孩子两个节点,所以我们需要将左右两个孩子节点进行比较,在得到较大的节点之后,再与它进行比较,如果它的子节点大,则将二者交换。并且不断的重复这样的操作,直到它没有叶子节点或者大于叶子节点停止。
四、用堆模拟实现优先级队列
public class priorityQueue {
public int[] elem;
public int usedSize;
public static final int DEFAULT_SIZE = 10;
public priorityQueue() {
this.elem = new int[DEFAULT_SIZE];
}
/**
* 建堆的时间复杂度为O(n)
* 不能只看代码去猜测
*/
public void createHeap(int[] array) {
//检查数组容量,不够就进行扩容
if(elem.length < array.length) {
elem = Arrays.copyOf(elem, array.length * 2);
}
for (int i = 0; i < array.length; i++) {
elem[i] = array[i];
usedSize++;
}
for (int i = (usedSize - 1 - 1) / 2; i >= 0; i--) {
shiftDown(i,usedSize - 1);
}
}
/**
* 调整每颗子树的时间复杂度为O(log n)
* root为每棵子树的根节点
* len为每棵子树的结束条件
* @return
*/
private void shiftDown(int root,int len) {
int child = root * 2 + 1;
while(child <= len) {
if(child + 1 < len && elem[child + 1] > elem[child]) {
child++;
}
if(elem[root] >= elem[child]) {
return;
} else {
int h = elem[root];
elem[root] = elem[child];
elem[child] = h;
root = child;
child = root * 2 + 1;
}
}
}
/**
* 入队之后要保证仍然为大根堆
* 所以我们插入到最后位置,然后向上调整
* @param val
*/
public void push(int val) {
//检查堆是否满了,满了进行扩容
if(isFull()) {
elem = Arrays.copyOf(elem,elem.length * 2);
}
elem[usedSize] = val;
usedSize++;
shiftUp(usedSize - 1);
}
private void shiftUp(int child) {
int parent = (child - 1) / 2;
while(child > 0) {
if(elem[parent] >= elem[child]) {
return;
}
int h = elem[child];
elem[child] = elem[parent];
elem[parent] = h;
child = parent;
parent = (child - 1) / 2;
}
}
public void pollHeap() {
//判断堆是否为空
if(isEmpty()) {
return;
}
int h = elem[0];
elem[0] = elem[usedSize - 1];
elem[usedSize - 1] = h;
usedSize--;
shiftDown(0,usedSize - 1);
}
public boolean isFull() {
return usedSize == elem.length;
}
public boolean isEmpty() {
return usedSize == 0;
}
public int peekHeap() {
//判断堆是否为空
if(isEmpty()) {
return -1;
}
return elem[0];
}
}
