智能优化算法期末复习(更新ing)
目录
一、GA遗传算法
二、ACO蚁群算法
三、PSO粒子群算法
四、SA模拟退火算法
五、ABC人工蜂群算法
六、综合
一、GA遗传算法
1.运算流程
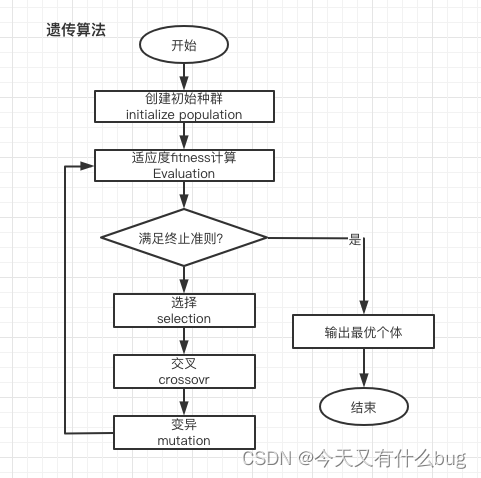
2.遗传算法适应值分配策略(基于目标函数的直接分配、基于排名的分配)

3.遗传算法在二进制问题(如0-1背包)和顺序问题(如TSP问题)的交叉和变异算子的实现
(1)单点交叉
左边部分都不变。

(2)部分交叉
现将所交叉部分提取出来,交换。剩下的根据情况分析是否放原位。

(3)变异:
0-1背包问题:直接0—>1,1—>0
TSP问题:
swap: 断掉4条边,连上4条边。
insert: 断掉一部分,将该部分插入某处。
inverse:将某一部分进行翻转,还是放在原处。

4.遗传算法的交叉概率和变异概率对算法行为的影响
①交叉概率Pc:较大的交叉概率可以增强遗传算法开辟新的搜索区域的能力,但高性能的模式遭到破坏的可能性增大;若交叉概率太低,遗传算法搜索可能陷入迟钝状态。
②变异概率Pm:一般低频度的变异可防止群体中重要基因的可能丢失,高频度的变异将使遗传算法趋于纯粹的随机搜索。
5.轮盘赌思想算法实现(遗传算法)
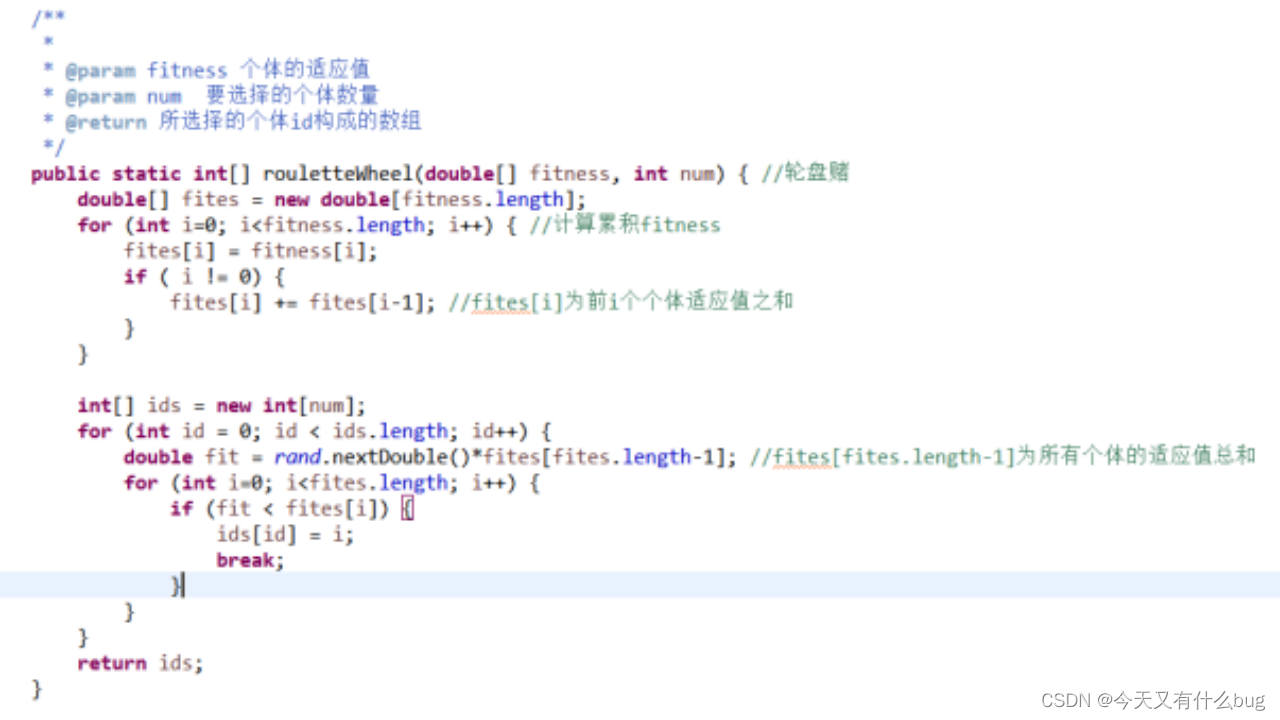
二、ACO蚁群算法
1.运算流程

三、PSO粒子群算法
1.运算流程
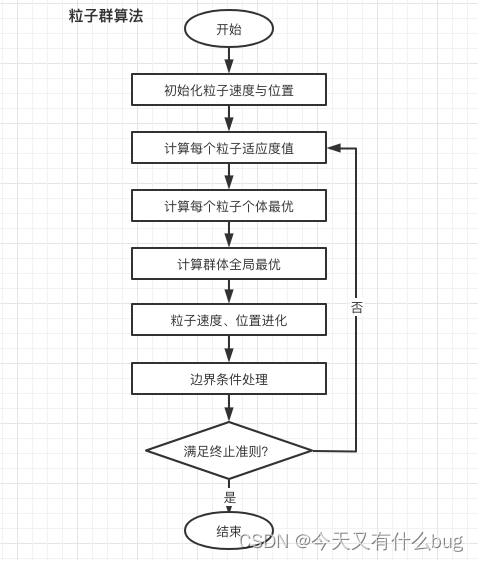
四、SA模拟退火算法
1.运算流程

2.模拟退火算法的的概率接收公式
系统从能量E1变化到E2,其对应的概率为:
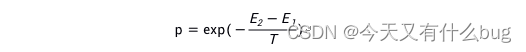
如果E2<E1,系统接收此状态;否则,以一个随机的概率接收或丢弃此状态。状态2被接收的概率为:
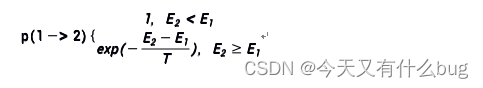
注:公式![]()
中的负号是求最小值的时候才有,若问题时求最大值,那么就没有负号,要懂得区别
3. 模拟退火算法的初始温度和降温系数(假设是几何降温)对算法行为的影响
(1)初始温度T0:T0越大,获得高质量解的概率越大。但是初温过高会导致计算时间增加,降低算法的收敛速度。
(2)降温速度α :α是[0,1]且非常接近1的常数,降温系数越大,温度下降越慢,算法收敛速度越慢,接收劣质解的概率越高,获得高质量解的概率越高。
4.模拟退火算法解决0-1背包问题
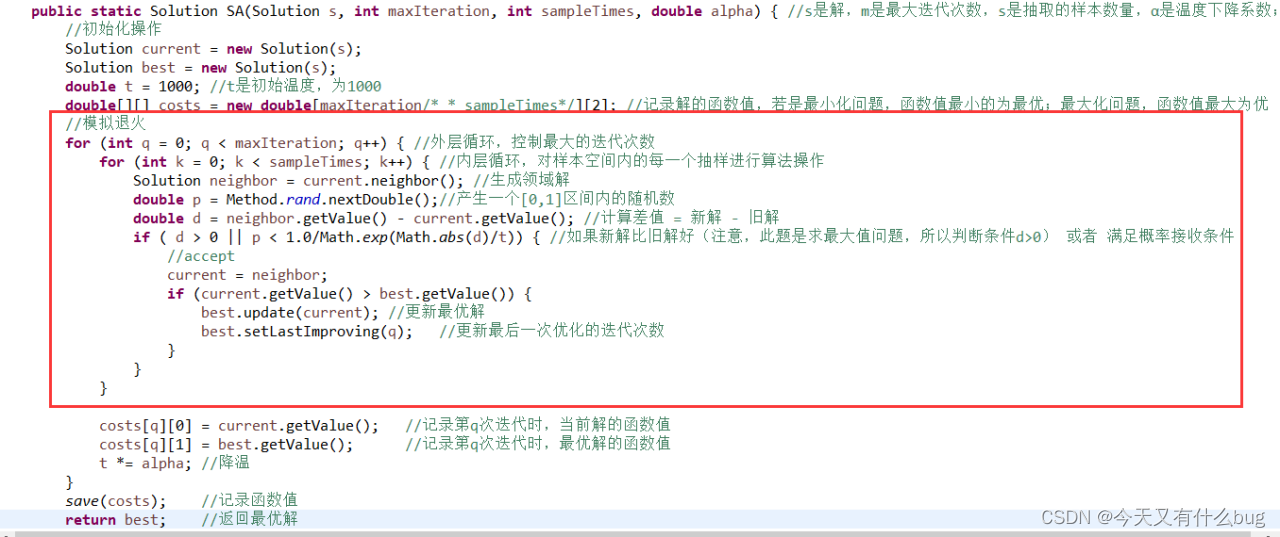
五、ABC人工蜂群算法
1.侦察蜂scout和观察蜂onlooker的作用
(1)侦察蜂的作用:当雇佣蜂太久没有更新解时(即陷入了局部解),则启动侦察蜂重新进行全局搜索,从而避免算法陷入局部最优解。
(2)观察蜂(跟随蜂)的作用:对雇佣蜂找到的局部解周围进行探索,即对局部解进行优化,寻找更优的局部最优解。
2.ABC算法的雇佣蜂(Employed bee)和观察峰(Onlooker)的数量。
①雇佣蜂(采蜜蜂)的数量越多,算法全局搜索性能越强,算法收敛越慢,但搜索到全局最优解的可能越大;
②观察蜂(跟随蜂)的数量越多,算法局部搜索性能越强,算法收敛越快,但越容易陷入局部最优解。
3.ABC算法的位置修改公式

4.从观察蜂的工作机制分析蜂群优化算法的正反馈机制。
观察蜂是跟随雇佣蜂,雇佣蜂找的蜜源越好,就会有越多的观察蜂跟随它,而观察蜂跟随的越多,那对雇佣蜂的函数值寻优次数(对蜜源的优化)就越多,那找到的解(蜜源)就会更优。从而形成了正反馈。
六、综合
1.区分metaheuristic和heuristic
(1)metaheuristic:元启发式算法,是一个通用的启发式策略,不借助于某种问题的特有条件,从而可以广泛运用。如GA、SA、PSO、ACO、ABC、DE。
(2)heuristic:启发式算法,针对特定条件下求解某个具体的问题。如爬山算法。
2.区分single solution-based和population-based的智能优化算法
(1)single solution-based的智能优化算法(迭代过程只有一个解):SA、TA
(2)population-based的智能优化算法:GA、ABC、PSO、ACO、DE
3.区分construction-based和iterative improvement-based的智能优化算法
(1)construction-based(每次都是从头开始构造新解):ACO解是通过一步步选出来的
(2)iterative improvement-based(迭代产生新解):GA、ABC、PSO、SA、DE、TA
4.区分组合优化问题、连续优化问题、约束优化问题等概念及我们使用的实例
(1)组合优化问题
①概念:具有离散变量的问题,我们称它为组合的。组合优化(Combinatorial Optimization)问题的目标是从组合问题的可行解集中求出最优解。
②实例:旅行商问题(Traveling Salesman Problem-TSP)、0-1背包问题(Knapsack Problem——KP)、度约束的最小生成树问题;
(2)连续优化问题
①概念:连续优化是求解连续变量的问题,其一般是求解一组实数,或者一个函数。
②实例:求解函数的最大值和最小值
(3)约束优化问题
①概念:约束优化问题是一类数学最优化问题,它由目标函数以及与目标函数中的变量相关的约束条件两部分组成,优化过程则为在约束条件下最优化(最大化或最小化)目标函数。
②实例:0-1KP、目标规划、度约束的问题
5.算法的简写
(1)模拟退火算法:Simulated Annealing,简称SA
(2)遗传算法:Genetic Algorithm,简称GA
(3)阈值接收算法:Threshold Algorithm,简称TA
(4)粒子群算法:Particle Swarm Optimization,简称PSO
(5)蚁群优化算法(简称蚁群算法):Ant Colony Optimization,简称ACO
(6)人工蜂群算法(简称蜂群算法):Artificial Bee Colony Algorithm, 简称ABC
(7)差分进化算法:Differential Evolution,简称DE
6.各种算法接收新解的方式(接收所有,只接收更好的,概率接收)
(1)概率接收劣质解:模拟退火算法(SA)、阈值接收算法(TA,确定性接收)
(2)只接收更好的:遗传算法(GA)、差分进化算法(DE)、人工蚁群优化算法(ACO)、蜂群优化算法(ABC)
(3)接收所有:粒子群优化算法(PSO)
7.。。
