当前位置：首页 > news >正文

基于MCMC的交通量逆建模（Matlab代码实现）

news 来源：原创 2024/11/2 12:23:37

🍒🍒🍒欢迎关注🌈🌈🌈

📝个人主页：我爱Matlab

👍点赞➕评论➕收藏 == 养成习惯（一键三连）🌻🌻🌻

🍌希望大家多多支持🍓~一起加油 🤗

💬语录：将来的我一定会感谢现在奋斗的自己！

🍁🥬🕒摘要🕒🥬🍁

马尔科夫链蒙特卡洛方法(Markov Chain Monte Carlo)，简称MCMC，产生于20世纪50年代早期，是在贝叶斯理论框架下，通过计算机进行模拟的蒙特卡洛方法(Monte Carlo)。该方法将马尔科夫(Markov)过程引入到Monte Carlo模拟中，实现抽样分布随模拟的进行而改变的动态模拟，弥补了传统的蒙特卡罗积分只能静态模拟的缺陷。MCMC是一种简单有效的计算方法，在很多领域得到广泛的应用，如统计物、贝叶斯(Bayes)问题、计算机问题等。

✨🔎⚡运行结果⚡🔎✨

💂♨️👨‍🎓Matlab代码👨‍🎓♨️💂

%this code simulates the true state
%used in the article simulations. It models the vehicle trajectories
%using the algorithm 2 in the article
close all
clear all
%set true state
deltaT=2/3600;
vmax=77;
rhomax=[180*5,170*4,160*5];
wf=16;

vmaxForMesh=80;
deltaX=deltaT*vmaxForMesh;
domainLengthInmiles=2;
numCells=domainLengthInmiles/deltaX;

timeSteps=500
vInitial=77*ones(numCells,1);
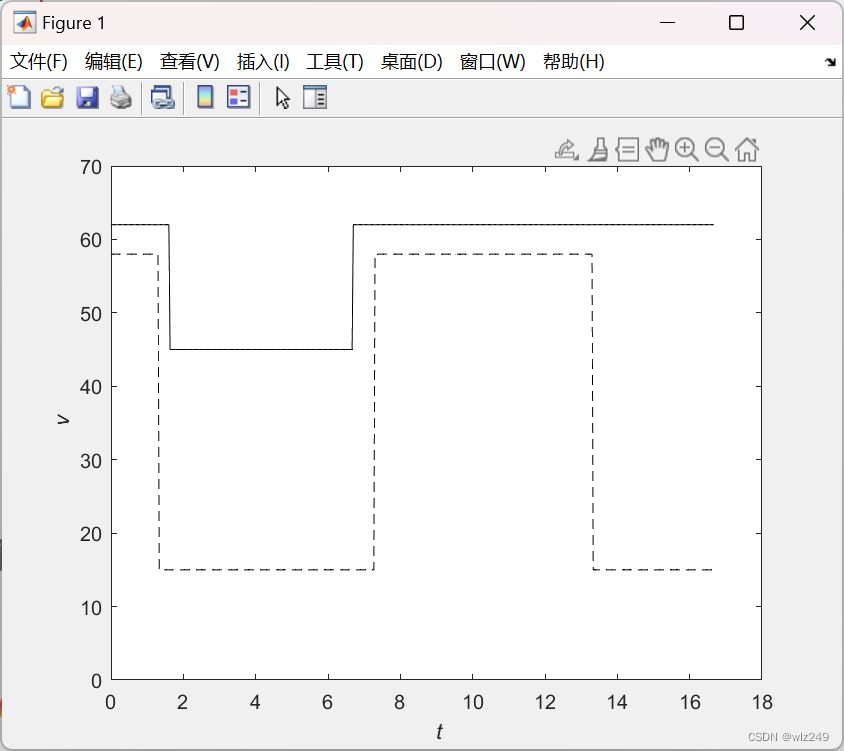
%% plot boundary conditions
figure
vUpstream=62*ones(timeSteps+1,1);
vUpstream(50:end-300)=45;
vDownstream=15*ones(timeSteps+1,1);
vDownstream(1:40)=58;
vDownstream(220:400)=58;
timeDisc=(0:deltaT:timeSteps*deltaT);
plot(timeDisc*60,vUpstream,'k -')
hold on
plot(timeDisc*60,vDownstream,'k --')
ylabel('\it v')
xlabel('\it t')
%legend('upstream','downstream')
set(gca,'Ylim',[0 70])
set(gcf, 'PaperUnits', 'inches');
papersize=[3 3];
set(gcf, 'PaperSize',papersize);
width=2.5;
height=2.5;
left=(papersize(1)-width)/2;
bottom=(papersize(2)-height)/2;
myfiguresize = [left,bottom,width,height];
set(gcf, 'PaperPosition', myfiguresize);
print('-dpsc2','figs/trueBoundaryConditions.eps')
system('epstopdf figs/trueBoundaryConditions.eps')
%axis tight
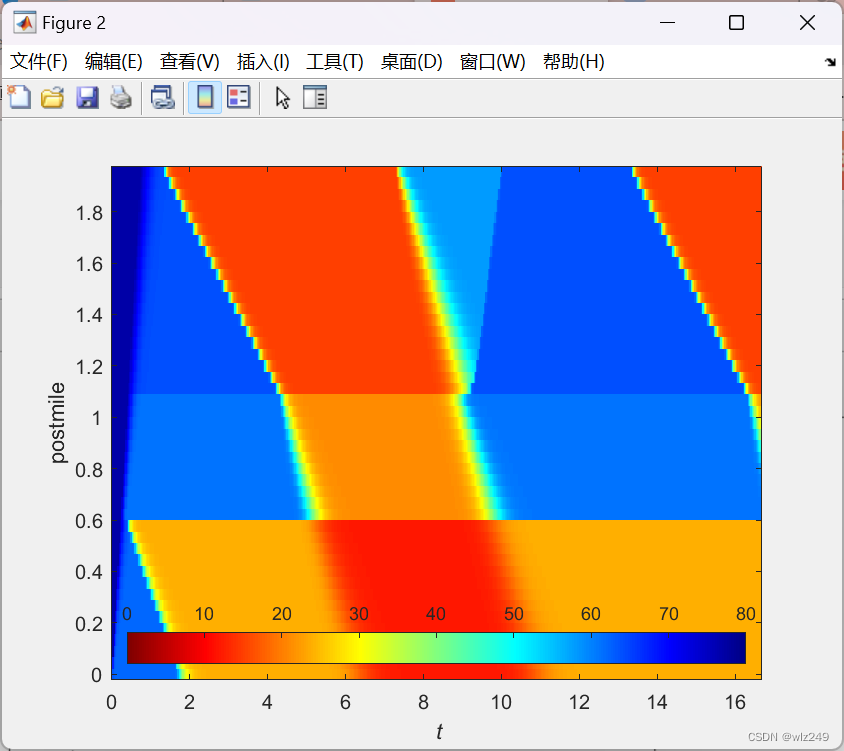
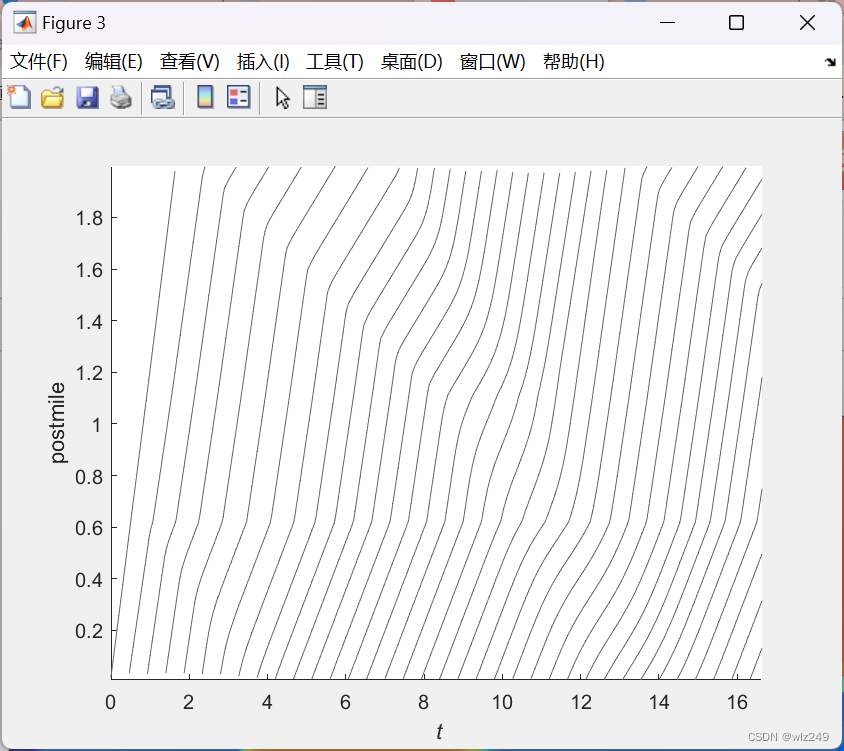
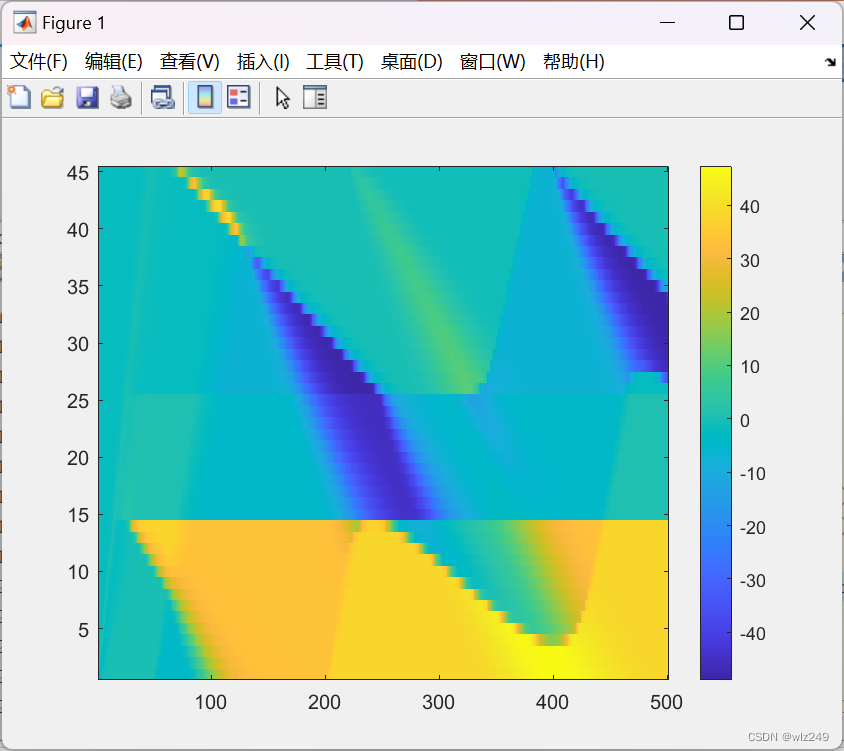
%% simulate v-field with CFL=0.5
numLanes=1*ones(size(vInitial));
numLanes(15:25)=1;
numLanes=[numLanes(1);numLanes;numLanes(end)];
dropLocation=(15:25);

rhoMaxVec=zeros(numCells,1);
rhoMaxVec(dropLocation)=rhomax(2);
rhoMaxVec(1:dropLocation(1)-1)=rhomax(1);
rhoMaxVec(dropLocation(end)+1:end)=rhomax(3);
rhoMaxVec=[rhoMaxVec(1);rhoMaxVec;rhoMaxVec(end)];

rhoCritVec=rhoMaxVec.*(wf/vmax);

vupdated=updatevHalfCFL(vInitial,deltaX,deltaT,timeSteps,vDownstream,vUpstream,rhoCritVec,vmax,wf*ones(numCells+2,1),rhoMaxVec,numLanes);