剑指offer

链表

注意几种情况

P=Q

将Q的value和next赋值给P,意味着P和Q同时指向Q的下一个节点

P.NEXT=Q

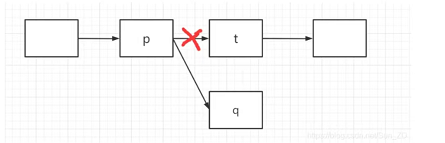
将Q赋值给P.NEXT，也就是说P的NEXT存放Q，P的下一个节点为Q同时，P与T连接中断

P=Q.NEXT

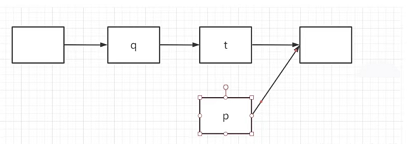
Q的下一个节点赋值给P,也就是将T复制而给P,也就是说T和P的value和next值相同，P和T同时指向 T的下一个元素。

链表基础

节点类

package com.geekmice.springbootlog.util.node;
// 节点类
public class Node {
     Integer data;
     Node next;
    public Node(Integer data){
        this.data=data;
    }

    public Node(Integer data, Node next) {
        this.data = data;
        this.next = next;
    }
}

链表类

// 链表类
package com.geekmice.springbootlog.util.node;

import org.slf4j.Logger;
import org.slf4j.LoggerFactory;

import javax.sound.sampled.TargetDataLine;

public class LinkedList {
    // 日志打印
    Logger logger = LoggerFactory.getLogger(LinkedList.class);

    // 链表头节点
    Node head = new Node(666, null);

    // 链表元素个数
    private int size;

    /**
     * @param node 待插入的节点
     * @Description 头插法
     */
    public void addFirst(Node node) {
        if (node != null) {
            node.next = head.next;
            head.next = node;
            size++;
        }
    }

    /**
     * @param node 待插入的节点
     * @Description 尾插法
     */
    public void addLast(Node node) {
        Node temp = head;
        while (true) {
            if (temp.next == null) {
                break;
            }
            temp = temp.next;
        }
        temp.next = node;
        size++;
    }


    /**
     * @param node
     * @Description 删除指定节点
     */
    public void removeNode(Node node) {
        Node temp = head.next;
        Node prev = head;
        while (true) {
            if (temp == null) {
                break;
            }
            if (temp.data == node.data) {
                prev.next = temp.next;
                size--;
                break;
            }
            temp = temp.next;
            prev = prev.next;
        }
    }

    /**
     * @param node 指定节点
     * @return 是否存在标志
     * @Description 判断指定节点是否存在
     */
    public Boolean contains(Node node) {
        Node temp = head;
        while (temp.next != null) {
            if (node.data == temp.data) {
                return true;
            }
            temp = temp.next;
        }
        return false;
    }

    /**
     * @param node
     * @return
     * @Description 获取指定节点所在位置
     */
    public int get(Node node) {
        Node temp = head;
        for (int i = 0; i < size; i++) {
            if (temp.data == node.data) {
                return i + 1;
            }
            temp = temp.next;
        }
        return -1;
    }

    /**
     * @param node
     * @Description 指定节点修改操作
     */
    public void set(Node node,int data) {
        Node temp = head;
        while (temp.next != null) {
            if (temp.data == node.data) {
                temp.data = data;
            }
            temp = temp.next;
        }
    }

    /**
     * @Description 打印链表
     */
    public String toString() {
        StringBuilder str = new StringBuilder();
        Node node = head;
        str.append("size: ").append(size);
        str.append(" link: [");
        while (node != null) {
            str.append(node.data);
            if (node != null) {
                str.append("--->");
            }
            node = node.next;
        }
        str.append("]");
        return str.toString();
    }
}

客户端测试

package com.geekmice.springbootlog.util.node;

import org.slf4j.Logger;
import org.slf4j.LoggerFactory;

public class Client {

    public static void main(String[] args) {
        Logger logger = LoggerFactory.getLogger(Client.class);
        LinkedList linkedList = new LinkedList();
        for (int i = 0; i < 10; i++) {
            linkedList.addLast(new Node(i));
        }
        logger.info("遍历链表：{}", linkedList.toString());
        linkedList.removeNode(new Node(1));
        logger.info("删除节点1：{}", linkedList.toString());
        linkedList.removeNode(new Node(0));
        logger.info("删除节点0：{}", linkedList.toString());
        linkedList.removeNode(new Node(9));
        logger.info("删除节点9：{}", linkedList.toString());
        logger.info("判断指定节点0是否存在，{}", linkedList.contains(new Node(0)));
        logger.info("判断指定节点3是否存在，{}", linkedList.contains(new Node(3)));
        logger.info("获取指定节点所在位置4，{}", linkedList.get(new Node(4)));
        logger.info("获取指定节点所在位置0，{}", linkedList.get(new Node(0)));
        linkedList.set(new Node(5),98);
        logger.info("遍历链表：{}", linkedList.toString());
    }
}

11:06:15.830 [main] INFO com.geekmice.springbootlog.util.node.Client - 遍历链表：size: 10 link: [666—>0—>1—>2—>3—>4—>5—>6—>7—>8—>9—>]
11:06:15.834 [main] INFO com.geekmice.springbootlog.util.node.Client - 删除节点1：size: 9 link: [666—>0—>2—>3—>4—>5—>6—>7—>8—>9—>]
11:06:15.834 [main] INFO com.geekmice.springbootlog.util.node.Client - 删除节点0：size: 8 link: [666—>2—>3—>4—>5—>6—>7—>8—>9—>]
11:06:15.834 [main] INFO com.geekmice.springbootlog.util.node.Client - 删除节点9：size: 7 link: [666—>2—>3—>4—>5—>6—>7—>8—>]
11:06:15.834 [main] INFO com.geekmice.springbootlog.util.node.Client - 判断指定节点0是否存在，false
11:06:15.834 [main] INFO com.geekmice.springbootlog.util.node.Client - 判断指定节点3是否存在，true
11:06:15.834 [main] INFO com.geekmice.springbootlog.util.node.Client - 获取指定节点所在位置4，4
11:06:15.835 [main] INFO com.geekmice.springbootlog.util.node.Client - 获取指定节点所在位置0，-1

1 从尾到头打印链表

方案一：非递归

listNode 是链表，只能从头遍历到尾，但是输出却要求从尾到头，这是典型的"先进后出"，我们可以想到栈！
ArrayList 中有个方法是 add(index,value)，可以指定 index 位置插入 value 值
所以我们在遍历 listNode 的同时将每个遇到的值插入到 list 的 0 位置，最后输出 listNode 即可得到逆序链表

代码实现

import java.util.*;
public class Solution {
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
        ArrayList<Integer> list = new ArrayList<>();
        ListNode tmp = listNode;
        while(tmp!=null){
            list.add(0,tmp.val);
            tmp = tmp.next;
        }
        return list;
    }
}

时间复杂度

方案二：递归

分析

借助系统的"栈"帮忙打印

代码实现

import java.util.*;
public class Solution {
    ArrayList<Integer> list = new ArrayList();
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
        if(listNode!=null){
            printListFromTailToHead(listNode.next);
            list.add(listNode.val);
        }
        return list;
    }
}

复杂度

方案三：普通数组存储

代码实现

public int[] print(ListNode node){
    // 思想：遍历链表，存储数组，数组倒序输出
	
	// 链表长度
	int len=0;
	while(node != null){
	    len++;
		node=node.next;
	}
	int[] array = new int[len];
	
	for(int i = 0 ; i<len;i++){
		node=node.next;
		array[i]=node.data;
	}
	int[] newArray = new int[len];
	for(int j=0;j<len;j++){
		newArray[j]=array[len-1-j];
	}
	return newArray;
}

方案三：递归

2 链表反转

问题描述

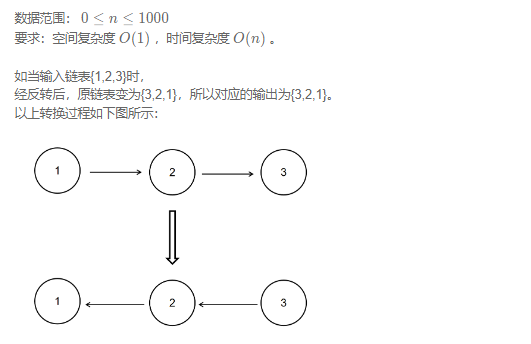
给定一个单链表的头结点pHead(该头节点是有值的，比如在下图，它的val是1)，长度为n，反转该链表后，返回新链表的表头。

示例

输入：{1,2,3}

返回值：{3,2,1}

输入：{}

返回值：{}

方案一：使用栈解决

链表的反转是老生常谈的一个问题了，同时也是面试中常考的一道题。最简单的一种方式就是使用栈，因为栈是先进后出的。

实现原理就是把链表节点一个个入栈，当全部入栈完之后再一个个出栈，出栈的时候在把出栈的结点串成一个新的链表。

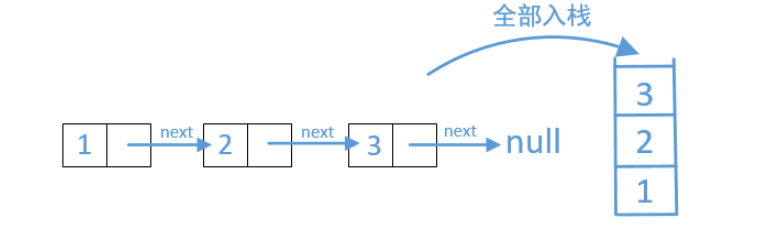
代码

import java.util.Stack;

public class Solution {
    public ListNode ReverseList(ListNode head) {
        Stack<ListNode> stack = new Stack<>();
        //把链表节点全部摘掉放到栈中
        while (head != null) {
            stack.push(head);
            head = head.next;
        }
        if (stack.isEmpty()){
            return null;
        }
        ListNode node = stack.pop();
        ListNode dummy = node;
        //栈中的结点全部出栈，然后重新连成一个新的链表
        while (!stack.isEmpty()) {
            ListNode tempNode = stack.pop();
            node.next = tempNode;
            node = node.next;
        }
        //最后一个结点就是反转前的头结点，一定要让他的next
        //等于空，否则会构成环
        node.next = null;
        return dummy;
    }
}

复杂度分析

时间复杂度：O(N),N表示链表长度

空间复杂度：O(N),栈空间

方案二：双指针迭代

分析

遍历链表同时，将当前节点的next指针指向前一个节点，由于节点没有引用前一个节点，因此必须事先存储前一个节点，在更改引用之前，需要存储后一个节点，最后返回头节点。

temp存放前一个节点地址

代码实现

public ListNode reverseList(ListNode head) {
    // pre指针：用来指向反转后的节点
    ListNode pre = null;
    // 当前节点
    ListNode cur = head ;
    while (cur != null) {
        // 指向当前节点下一个节点
        ListNode temp = cur.next;
        // 当前节点指向前一个节点
        cur.next=pre;
        // 更新pre
        pre=cur;
        // 更新当前节点
        cur=temp;
    }
    //返回新链表
    return pre;
}

复杂度分析

时间复杂度：O(N),N表示链表长度，需要遍历链表一次

空间复杂度：O(1)，常数空间复杂度

方案三：递归

终止条件是当前节点或者下一个节点==null
在函数内部，改变节点的指向，也就是 head 的下一个节点指向 head 递归函数那句
head.next.next = head
很不好理解，其实就是 head 的下一个节点指向head。
递归函数中每次返回的 cur 其实只最后一个节点，在递归函数内部，改变的是当前节点的指向。

public class Solution {
	public ListNode reverseList(ListNode head) {
		//递归终止条件是当前为空，或者下一个节点为空
		if(head==null || head.next==null) {
			return head;
		}
		//这里的cur就是最后一个节点
		ListNode cur = reverseList(head.next);
		//这里请配合动画演示理解
		//如果链表是 1->2->3->4->5，那么此时的cur就是5
		//而head是4，head的下一个是5，下下一个是空
		//所以head.next.next 就是5->4
		head.next.next = head;
		//防止链表循环，需要将head.next设置为空
		head.next = null;
		//每层递归函数都返回cur，也就是最后一个节点
		return cur;
	}
}

3 反转链表一部分

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

注意：这里要提醒大家的是，链接什么时候切断，什么时候补上去，先后顺序一定要想清楚，如果想不清楚，可以在纸上模拟，让思路清晰

示例 1：

输入：head = [1,2,3,4,5], left = 2, right = 4
输出：[1,4,3,2,5]

示例 2：

输入：head = [5], left = 1, right = 1
输出：[5]

方法一：穿针引线

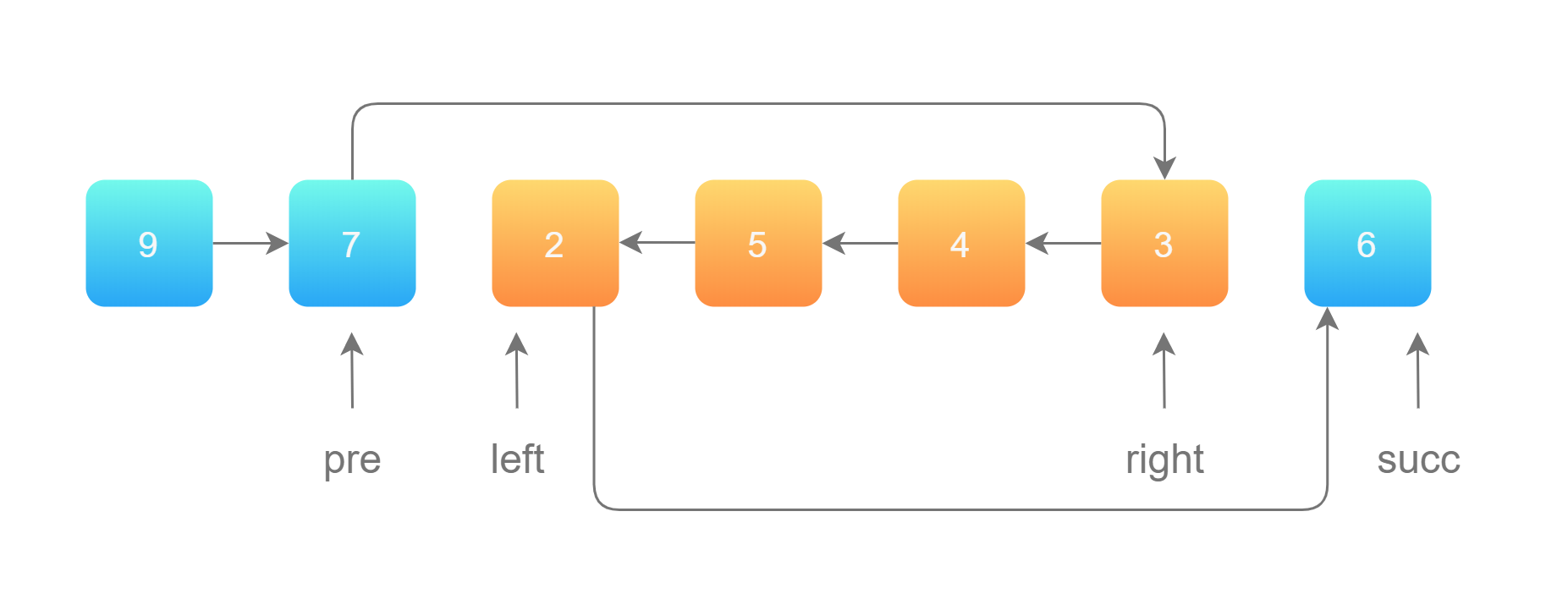
class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        // 因为头节点有可能发生变化，使用虚拟头节点可以避免复杂的分类讨论
        ListNode dummyNode = new ListNode(-1);
        dummyNode.next = head;

        ListNode pre = dummyNode;
        // 第 1 步：从虚拟头节点走 left - 1 步，来到 left 节点的前一个节点
        // 建议写在 for 循环里，语义清晰
        for (int i = 0; i < left - 1; i++) {
            pre = pre.next;
        }

        // 第 2 步：从 pre 再走 right - left + 1 步，来到 right 节点
        ListNode rightNode = pre;
        for (int i = 0; i < right - left + 1; i++) {
            rightNode = rightNode.next;
        }

        // 第 3 步：切断出一个子链表（截取链表）
        ListNode leftNode = pre.next;
        ListNode curr = rightNode.next;

        // 注意：切断链接
        pre.next = null;
        rightNode.next = null;

        // 第 4 步：同第 206 题，反转链表的子区间
        reverseLinkedList(leftNode);

        // 第 5 步：接回到原来的链表中
        pre.next = rightNode;
        leftNode.next = curr;
        return dummyNode.next;
    }

    private void reverseLinkedList(ListNode head) {
        // 也可以使用递归反转一个链表
        ListNode pre = null;
        ListNode cur = head;

        while (cur != null) {
            ListNode next = cur.next;
            cur.next = pre;
            pre = cur;
            cur = next;
        }
    }
}

复杂度分析

时间复杂度：O(N)，其中N表示节点总数，最坏情况，遍历整个链表

空间复杂度：O(1)

方法二：一次遍历「穿针引线」反转链表（头插法）

class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        // 设置 dummyNode 是这一类问题的一般做法
        ListNode dummyNode = new ListNode(-1);
        dummyNode.next = head;
        ListNode pre = dummyNode;
        for (int i = 0; i < left - 1; i++) {
            pre = pre.next;
        }
        ListNode cur = pre.next;
        ListNode next;
        for (int i = 0; i < right - left; i++) {
            next = cur.next;
            cur.next = next.next;
            next.next = pre.next;
            pre.next = next;
        }
        return dummyNode.next;
    }
}

复杂度分析

时间复杂度：O(N)，其中 N 是链表总节点数。最多只遍历了链表一次，就完成了反转。

空间复杂度：O(1)

4 K 个一组翻转链表

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

实例1

输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

实例2

输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

方法一：

代码实现

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        if (head == null || head.next == null){
            return head;
        }
        //定义一个假的节点。
        ListNode dummy=new ListNode(0);
        //假节点的next指向head。
        // dummy->1->2->3->4->5
        dummy.next=head;
        //初始化pre和end都指向dummy。pre指每次要翻转的链表的头结点的上一个节点。end指每次要翻转的链表的尾节点
        ListNode pre=dummy;
        ListNode end=dummy;

        while(end.next!=null){
            //循环k次，找到需要翻转的链表的结尾,这里每次循环要判断end是否等于空,因为如果为空，end.next会报空指针异常。
            //dummy->1->2->3->4->5 若k为2，循环2次，end指向2
            for(int i=0;i<k&&end != null;i++){
                end=end.next;
            }
            //如果end==null，即需要翻转的链表的节点数小于k，不执行翻转。
            if(end==null){
                break;
            }
            //先记录下end.next,方便后面链接链表
            ListNode next=end.next;
            //然后断开链表
            end.next=null;
            //记录下要翻转链表的头节点
            ListNode start=pre.next;
            //翻转链表,pre.next指向翻转后的链表。1->2 变成2->1。 dummy->2->1
            pre.next=reverse(start);
            //翻转后头节点变到最后。通过.next把断开的链表重新链接。
            start.next=next;
            //将pre换成下次要翻转的链表的头结点的上一个节点。即start
            pre=start;
            //翻转结束，将end置为下次要翻转的链表的头结点的上一个节点。即start
            end=start;
        }
        return dummy.next;


    }
    //链表翻转
    // 例子：   head： 1->2->3->4
    public ListNode reverse(ListNode head) {
         //单链表为空或只有一个节点，直接返回原单链表
        if (head == null || head.next == null){
            return head;
        }
        //前一个节点指针
        ListNode preNode = null;
        //当前节点指针
        ListNode curNode = head;
        //下一个节点指针
        ListNode nextNode = null;
        while (curNode != null){
            nextNode = curNode.next;//nextNode 指向下一个节点,保存当前节点后面的链表。
            curNode.next=preNode;//将当前节点next域指向前一个节点   null<-1<-2<-3<-4
            preNode = curNode;//preNode 指针向后移动。preNode指向当前节点。
            curNode = nextNode;//curNode指针向后移动。下一个节点变成当前节点
        }
        return preNode;

    }

}

复杂度分析

时间复杂度：O(N*K),最好情况O(N),最坏情况O(N^2)

空间复杂度：O(1),除了几个必须节点指针，没有占用其他空间

5 合并两个排序的链表

题目描述

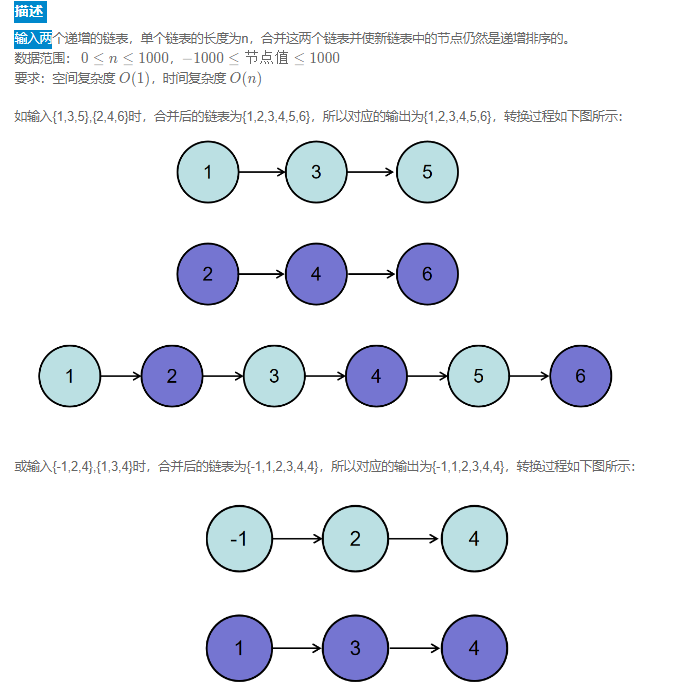
方案一：递归

思路整理：

简单地理一下思路：

• 从头结点开始考虑，比较两表头结点的值，值较小的list的头结点后面接merge好的链表（进入递归了）；
• 若两链表有一个为空，返回非空链表，递归结束；
• 当前层不考虑下一层的细节，当前层较小的结点接上该结点的next与另一结点merge好的表头就ok了；
• 每层返回选定的较小结点就ok；

重新整理一下：

• 终止条件：两链表其中一个为空时，返回另一个链表；
• 当前递归内容：若list1.val <= list2.val 将较小的list1.next与merge后的表头连接，即list1.next = Merge(list1.next,list2); list2.val较大时同理；
• 每次的返回值：排序好的链表头；

代码实现

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode Merge(ListNode list1,ListNode list2) {
        if(list1==null){
            return list2;
        }
        else if(list2==null){
            return list1;
        }
        if(list2.val>list1.val){
            list1.next = Merge(list1.next,list2);
            return list1;
        }
        else{
            list2.next = Merge(list1,list2.next);
            return list2;
        }
    }
}

复杂度分析

时间复杂度O(N+M)：M N分别表示list1, list2的长度

空间复杂度O(N+M)：迭代次数占用空间

方案二：迭代

• 创建一个虚拟结点和一个哨兵结点
• 当list1与list2都不为null时循环
• 哪个的val小哪个赋给虚拟结点的next，虚拟结点后移。
• 退出循环后，哪个list不为空，哪个结点（包括剩下的）给虚拟结点的next
• 最后返回哨兵结点的next

代码实现

public class Solution {
    public ListNode Merge(ListNode list1,ListNode list2) {
        ListNode dummy = new ListNode(-1);
        ListNode res = dummy;
        // 必须保证两个list都不为空
        while(list1 != null && list2 != null) {
            if(list1.val > list2.val) {
                dummy.next = list2;
                list2 = list2.next;
                dummy = dummy.next;
            } else if(list1.val <= list2.val) {
                dummy.next = list1;
                list1 = list1.next;
                dummy = dummy.next;
            }
        }
        // list1后面还有，就把剩下的全部拿走
        if(list1 != null) {
            dummy.next = list1;
        }
        if(list2 != null) {
            dummy.next = list2;
        }
        return res.next;
    }
}

复杂度分析

时间复杂度：两个表都遍历了一遍，时间复杂度O(M+N)

空间复杂度：初始化虚拟虚拟头结点，使每一个结点都有一个前驱结点便于循环，O(1)

6 合并K个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

输入：lists = []
输出：[]

示例 3：

输入：lists = [[]]
输出：[]

方案一：顺序合并

思路：我们可以想到一种最朴素的方法：用一个变量 ans 来维护以及合并的链表，第 i 次循环把第 i 个链表和 ans 合并，答案保存到ans 中。

核心：依次合并两个链表存放ans，合并之后新链表再和下一个链表合并存放ans，依次合并

代码实现

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        ListNode ans = null;
        for (int i = 0; i < lists.length; ++i) {
            ans = mergeTwoLists(ans, lists[i]);
        }
        return ans;
    }

    public ListNode mergeTwoLists(ListNode a, ListNode b) {
        // 如果链表a空返回b链表
        // 如果链表b空返回a链表
        if (a == null || b == null) {
            return a != null ? a : b;
        }
        // 定义头节点
        ListNode head = new ListNode(0);
        ListNode tail = head, aPtr = a, bPtr = b;
        // 类似于两个有序链表合并
        while (aPtr != null && bPtr != null) {
            if (aPtr.val < bPtr.val) {
                tail.next = aPtr;
                aPtr = aPtr.next;
            } else {
                tail.next = bPtr;
                bPtr = bPtr.next;
            }
            tail = tail.next;
        }
        tail.next = (aPtr != null ? aPtr : bPtr);
        return head.next;
    }
}

复杂度分析

7 两个链表的第一个公共结点

输入两个无环的单向链表，找出它们的第一个公共结点，如果没有公共节点则返回空。（注意因为传入数据是链表，所以错误测试数据的提示是用其他方式显示的，保证传入数据是正确的）

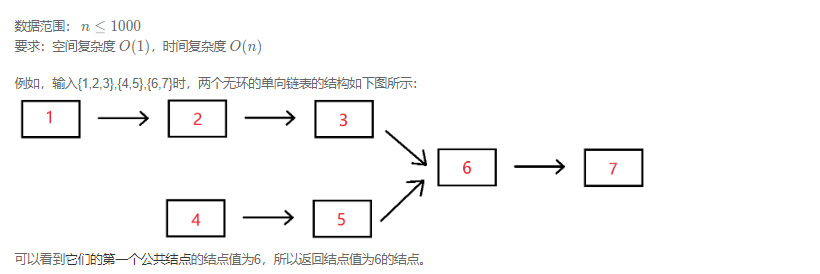
可以看到它们的第一个公共结点的结点值为6，所以返回结点值为6的结点。

简要描述：输入分为是3段，第一段是第一个链表的非公共部分，第二段是第二个链表的非公共部分，第三段是第一个链表和第二个链表的公共部分。 后台会将这3个参数组装为两个链表，并将这两个链表对应的头节点传入到函数FindFirstCommonNode里面，用户得到的输入只有pHead1和pHead2。

返回值描述：返回传入的pHead1和pHead2的第一个公共结点，后台会打印以该节点为头节点的链表。

示例1

{1,2,3},{4,5},{6,7}

{6,7}

说明：

第一个参数{1,2,3}代表是第一个链表非公共部分，第二个参数{4,5}代表是第二个链表非公共部分，最后的{6,7}表示的是2个链表的公共部分
这3个参数最后在后台会组装成为2个两个无环的单链表，且是有公共节点的   

示例2

输入：{1},{2,3},{}

返回值：{}

说明：2个链表没有公共节点 ,返回null，后台打印{}

方案一：set

解题思路：这是一种「从前往后」找的方式。

使用 Set 数据结构，先对某一条链表进行遍历，同时记录下来所有的节点。

然后在对第二链条进行遍历时，检查当前节点是否在 Set 中出现过，第一个在 Set 出现过的节点即是交点。

import java.util.*;
/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
        Set<ListNode> set = new HashSet<ListNode>();
        while (pHead1 != null) {
            set.add(pHead1);
            pHead1 = pHead1.next;
        }
        while (pHead2 != null && !set.contains(pHead2)) {
            pHead2 = pHead2.next;

        }
        return pHead2;
    }
}

时间复杂度，空间复杂度

方案二：等值法

这是「差值法」的另外一种实现形式，原理同样利用「两条链表在相交节点后面的部分完全相同」。

我们令第一条链表相交节点之前的长度为 a，第二条链表相交节点之前的长度为 b，相交节点后的公共长度为 c（注意 c 可能为 00，即不存在相交节点）。

分别对两条链表进行遍历：

• 当第一条链表遍历完，移动到第二条链表的头部进行遍历；
• 当第二条链表遍历完，移动到第一条链表的头部进行遍历。

如果存在交点：第一条链表首次到达「第一个相交节点」的充要条件是第一条链表走了 a + c + b步，由于两条链表同时出发，并且步长相等，因此当第一条链表走了 a + c + b 步时，第二条链表同样也是走了 a + c + b步，即 第二条同样停在「第一个相交节点」的位置。

如果不存在交点：两者会在走完 a + c + b + c 之后同时变为 null，退出循环。

import java.util.*;
public class Solution {
    public ListNode FindFirstCommonNode(ListNode a, ListNode b) {
        ListNode ta = a, tb = b;
        while (ta != tb) {
            ta = ta == null ? b : ta.next;
            tb = tb == null ? a : tb.next;
        }
        return ta;
    }
}

8 删除链表中重复的结点

题目描述

在一个排序的链表中，存在重复的结点，请删除该链表中重复的结点，重复的结点不保留，返回链表头指针。 例如，链表 1->2->3->3->4->4->5 处理后为 1->2->5

要求

示例

输入：{1,2,3,3,4,4,5}

返回值：{1,2,5}

输入：{1,1,1,8}

返回值：{8}

方案一：直接比较删除

题目主要信息

• 在一个非降序的链表中，存在重复的节点，删除该链表中重复的节点
• 重复的节点一个元素也不保留

思路

这是一个升序链表，重复的节点都连在一起，我们就可以很轻易地比较到重复的节点，然后将所有的连续相同的节点都跳过，连接不相同的第一个节点。

具体做法

• step 1：给链表前加上表头，方便可能的话删除第一个节点。

ListNode res = new ListNode(0); //在链表前加一个表头
res.next = pHead;

• step 2：遍历链表，每次比较相邻两个节点，如果遇到了两个相邻节点相同，则新开内循环将这一段所有的相同都遍历过去。
• step 3：在step 2中这一连串相同的节点前的节点直接连上后续第一个不相同值的节点。
• step 4：返回时去掉添加的表头。

代码

public class Solution {
    public ListNode deleteDuplication(ListNode pHead) {
        //空链表
        if(pHead == null) 
            return null;
        ListNode res = new ListNode(0);
        //在链表前加一个表头
        res.next = pHead; 
        ListNode cur = res;
        while(cur.next != null && cur.next.next != null){ 
            //遇到相邻两个节点值相同
            if(cur.next.val == cur.next.next.val){ 
                int temp = cur.next.val;
                //将所有相同的都跳过
                while (cur.next != null && cur.next.val == temp) 
                    cur.next = cur.next.next;
            }
            else 
                cur = cur.next;
        }
        //返回时去掉表头
        return res.next; 
    }
}

复杂度分析

方案二：哈希表

思路

这道题幸运的是链表有序，我们可以直接与旁边的元素比较，然后删除重复。那我们扩展一点，万一遇到的链表无序呢？我们这里给出一种通用的解法，有序无序都可以使用，即利用哈希表来统计是否重复。

具体做法

• step 1：遍历一次链表用哈希表记录每个节点值出现的次数。
• step 2：在链表前加一个节点值为0的表头，方便可能的话删除表头元素。
• step 3：再次遍历该链表，对于每个节点值检查哈希表中的计数，只留下计数为1的，其他情况都删除。
• step 4：返回时去掉增加的表头。

代码实现

import java.util.*;
public class Solution {
    public ListNode deleteDuplication(ListNode pHead) {
        //空链表
        if(pHead == null) 
            return null;
        Map<Integer,Integer> mp = new HashMap<>();
        ListNode cur = pHead;
        //遍历链表统计每个节点值出现的次数
        while(cur != null){ 
            if(mp.containsKey(cur.val))
                mp.put(cur.val, (int)mp.get(cur.val) + 1);
            else
                mp.put(cur.val,1);
            cur = cur.next;
        }
        ListNode res = new ListNode(0);
        //在链表前加一个表头
        res.next = pHead; 
        cur = res;
        //再次遍历链表
        while(cur.next != null){
            //如果节点值计数不为1 
            if(mp.get(cur.next.val) != 1) 
                //删去该节点
                cur.next = cur.next.next; 
            else
                cur = cur.next; 
        }
        //去掉表头
        return res.next; 
    }
}

复杂度分析

9 删除链表中元素

题目描述：给定单向链表的头指针和一个要删除的节点的值，定义一个函数删除该节点。返回删除后的链表的头节点。

1.此题对比原题有改动

2.题目保证链表中节点的值互不相同

3.该题只会输出返回的链表和结果做对比，所以若使用 C 或 C++ 语言，你不需要 free 或 delete 被删除的节点

数据范围:

0<=链表节点值<=10000

0<=链表长度<=10000

题目的主要信息：

• 给定单链表的一个头，删除该链表指定节点
• 该链表所有元素不同

方案一：直接删除

import java.util.*;

/*
 * public class ListNode {
 *   int val;
 *   ListNode next = null;
 *   public ListNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param head ListNode类 
     * @param val int整型 
     * @return ListNode类
     */
    public ListNode d eleteNode (ListNode head, int val) {
        // 存储头结点
        ListNode res = head;
        ListNode pre = head;
        ListNode after = head.next;
        while(pre != null) {
            if(pre == head && pre.val == val) {
                return pre.next;
            }
            if(after.val == val) {
                pre.next = after.next;
                break;
            }
            pre = after;
            after = after.next;
        }
        return res;
    }
}

10 链表中倒数最后k个节点

题目要求：输入一个长度为n的链表，链表中元素未能a(i)，返回链表中倒数第k个节点，如果链表长度小于k，返回长度为0的链表

时间空间复杂度：O(n)

示例说明：

输入：{1,2,3,4,5} 2 返回 4

输入：{1} 8 返回 {}

方案一：快慢指针

思路：

这题要求链表的倒数第k个节点，最简单的方式就是使用两个指针，第一个指针先移动k步，然后第二个指针再从头开始，这个时候这两个指针同时移动，当第一个指针到链表的末尾的时候，返回第二个指针即可。注意，如果第一个指针还没走k步的时候链表就为空了，我们直接返回null即可。

    public ListNode FindKthToTail(ListNode pHead, int k) {
        if (pHead == null)
            return pHead;
        ListNode first = pHead;
        ListNode second = pHead;
        //第一个指针先走k步7
        while (k-- > 0) {
            if (first == null){
                return null;
            }                
            first = first.next;
        }
        //然后两个指针在同时前进
        while (first != null) {
            first = first.next;
            second = second.next;
        }
        return second;
    }

方案二：先获取链表长度再取值

链表不能逆向遍历，也不能直接访问。但是对于倒数第kkk个位置，我们只需要知道是正数多少位还是可以直接遍历得到的。

• step 1：可以先遍历一次链表找到链表的长度。
• step 2：然后比较链表长度是否比k小，如果比k小返回一个空节点。
• step 3：如果链表足够长，则我们从头节点往后遍历n−k次即可找到所求。

import java.util.*;
public class Solution {
    public ListNode FindKthToTail (ListNode pHead, int k) {
        int n = 0;
        ListNode p = pHead;
         //遍历链表，统计链表长度
        while(p != null){
            n++;
            p = p.next;
        }
        //长度过小，返回空链表
        if(n < k){
            return null;
        }                         
        p = pHead;
        //遍历n-k次
        for(int i = 0; i < n - k; i++){
            p = p.next;
        }             
        return p;
    }
}

11 链表中环的入口节点

给一个长度为n链表，若其中包含环，请找出该链表的环的入口结点，否则，返回null。

例如，输入{1,2},{3,4,5}时，对应的环形链表如下图所示：

可以看到环的入口结点的结点值为3，所以返回结点值为3的结点。

输入描述

输入分为2段，第一段是入环前的链表部分，第二段是链表环的部分，后台会根据第二段是否为空将这两段组装成一个无环或者有环单链表

返回值描述

返回链表的环的入口结点即可，我们后台程序会打印这个结点对应的结点值；若没有，则返回对应编程语言的空结点即可。

示例1

输入：{1,2}，{3,4,5}

返回值：3

说明：返回唤醒链表入口节点，我们后台程序打印环形链表入口节点，即3

示例2

输入：{1}，{}

返回值：null

说明：没有环，返回对应编程语言的空节点，打印 null

示例3

输入：{}，{2}

返回值：2

说明：环的部分只有一个节点，所以返回环形链表入口节点，打印该节点

方法一：快慢指针

双指针指的是在遍历对象的过程中，不是普通的使用单个指针进行访问，而是使用两个指针（特殊情况甚至可以多个），两个指针或是同方向访问两个链表、或是同方向访问一个链表（快慢指针）、或是相反方向扫描（对撞指针），从而达到我们需要的目的。

思路：

根据题干，不说别的，我们能发现这道题需要完成两个任务：

1. 判断链表是否有环。
2. 在有环的链表中找到环的入口。

对于第一个任务，可以参考判断链表中是否有环，主要思想是利用环没有末尾NULL，后半部分一定是环，然后快慢双指针相遇就代表有环

• step 1：使用BM6.判断链表中是否有环中的方法判断链表是否有环，并找到相遇的节点。
• step 2：慢指针继续在相遇节点，快指针回到链表头，两个指针同步逐个元素逐个元素开始遍历链表。
• step 3：再次相遇的地方就是环的入口。

再次相遇即是环入口分析

从头结点到入口节点前一个节点a个，环中有b个节点，快指针走过节点数f，慢指针走过节点数s

结论

f=2*s 快指针走过的节点数一定是慢指针的两倍

f=s+nb 两者相遇时候，快指针一定走过n圈

=》

s=nb

所以，当两者相遇，慢指针已经走了nb步，我们知道要想找到入口节点，需要a+nb步（入口节点之前步数+n圈环节点个数），慢指针已经走了nb步，所有这时候快指针放在表头，慢指针在相遇节点，只需要快慢指针同时走，a步就能找到入口节点。

代码实现

public class Solution {
    //判断有没有环，返回相遇的地方
    public ListNode hasCycle(ListNode head) {
        //先判断链表为空的情况
        if(head == null) {
            return null;
        }
        //快慢双指针
        ListNode fast = head; 
        ListNode slow = head;
        //如果没环快指针会先到链表尾
        while(fast != null && fast.next != null){ 
            //快指针移动两步
            fast = fast.next.next; 
            //慢指针移动一步
            slow = slow.next; 
            //相遇则有环，返回相遇的位置
            if(fast == slow) {
                return slow;
            }                
        }
        //到末尾说明没有环，返回null
        return null; 
    }
    
    public ListNode EntryNodeOfLoop(ListNode pHead) {
        ListNode slow = hasCycle(pHead);
        //没有环
        if(slow == null) 
            return null;
        //快指针回到表头
        ListNode fast = pHead; 
        //再次相遇即是环入口
        while(fast != slow){ 
            fast = fast.next;
            slow = slow.next;
        }
        return slow;
    }
}

12 分隔链表

给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。

你应当 保留 两个分区中每个节点的初始相对位置。

示例 1：

输入：head = [1,4,3,2,5,2], x = 3
输出：[1,2,2,4,3,5]

示例 2：

输入：head = [2,1], x = 2
输出：[1,2]

方法一：

代码实现

class Solution {
    public ListNode partition(ListNode head, int x) {
        ListNode small = new ListNode(0);
        ListNode smallHead = small;
        ListNode large = new ListNode(0);
        ListNode largeHead = large;
        while (head != null) {
            if (head.val < x) {
                small.next = head;
                small = small.next;
            } else {
                large.next = head;
                large = large.next;
            }
            head = head.next;
        }
        large.next = null;
        small.next = largeHead.next;
        return smallHead.next;
    }
}

复杂度分析

时间复杂度：O(n),n表示原来链表长度，我们对链表遍历一次

空间复杂度：O(1)

13 回文链表

给定一个链表的 头节点 head **，**请判断其是否为回文链表。

如果一个链表是回文，那么链表节点序列从前往后看和从后往前看是相同的。

示例1

输入: head = [1,2,3,3,2,1]
输出: true

示例2

输入: head = [1,2]
输出: false

方法一：双指针

一共为两个步骤：

复制链表值到数组列表中。
使用双指针法判断是否为回文。
第一步，我们需要遍历链表将值复制到数组列表中。我们用 currentNode 指向当前节点。每次迭代向数组添加 currentNode.val，并更新 currentNode = currentNode.next，当 currentNode = null 时停止循环。

执行第二步的最佳方法取决于你使用的语言。在 Python 中，很容易构造一个列表的反向副本，也很容易比较两个列表。而在其他语言中，就没有那么简单。因此最好使用双指针法来检查是否为回文。我们在起点放置一个指针，在结尾放置一个指针，每一次迭代判断两个指针指向的元素是否相同，若不同，返回 false；相同则将两个指针向内移动，并继续判断，直到两个指针相遇。

在编码的过程中，注意我们比较的是节点值的大小，而不是节点本身。正确的比较方式是：node_1.val == node_2.val，而 node_1 == node_2 是错误的。

代码实现

class Solution {
    public boolean isPalindrome(ListNode head) {
        List<Integer> vals = new ArrayList<Integer>();

        // 将链表的值复制到数组中
        ListNode currentNode = head;
        while (currentNode != null) {
            vals.add(currentNode.val);
            currentNode = currentNode.next;
        }

        // 使用双指针判断是否回文
        int front = 0;
        int back = vals.size() - 1;
        while (front < back) {
            if (!vals.get(front).equals(vals.get(back))) {
                return false;
            }
            front++;
            back--;
        }
        return true;
    }
}

class Solution {
    public boolean isPalindrome(ListNode head) {
        List<Integer> vals = new ArrayList<Integer>();

        // 将链表的值复制到数组中
        ListNode currentNode = head;
        while (currentNode != null) {
            vals.add(currentNode.val);
            currentNode = currentNode.next;
        }

        // 使用双指针判断是否回文
        int front = 0;
        int back = vals.size() - 1;
        while (front < back) {
            if (!vals.get(front).equals(vals.get(back))) {
                return false;
            }
            front++;
            back--;
        }
        return true;
    }
}

复杂度分析

时间复杂度：O(n)，其中 n 指的是链表的元素个数。
第一步： 遍历链表并将值复制到数组中，O(n)。
第二步：双指针判断是否为回文，执行了 O(n/2) 次的判断，即 O(n)
总的时间复杂度：O(2n)=O(n)
空间复杂度：O(n))，其中n 指的是链表的元素个数，我们使用了一个数组列表存放链表的元素值。

方法二：递归

算法 currentNode 指针是先到尾节点，由于递归的特性再从后往前进行比较。frontPointer 是递归函数外的指针。若 currentNode.val != frontPointer.val 则返回 false。反之，frontPointer 向前移动并返回 true

代码实现

class Solution {
    private ListNode frontPointer;

    private boolean recursivelyCheck(ListNode currentNode) {
        if (currentNode != null) {
            if (!recursivelyCheck(currentNode.next)) {
                return false;
            }
            if (currentNode.val != frontPointer.val) {
                return false;
            }
            frontPointer = frontPointer.next;
        }
        return true;
    }

    public boolean isPalindrome(ListNode head) {
        frontPointer = head;
        return recursivelyCheck(head);
    }
}

复杂度分析

时间复杂度：O(n)，其中 n 指的是链表的大小。
空间复杂度：O(n)，其中 n 指的是链表的大小。

我们要理解计算机如何运行递归函数，在一个函数中调用一个函数时，计算机需要在进入被调用函数之前跟踪它在当前函数中的位置（以及任何局部变量的值），通过运行时存放在堆栈中来实现（堆栈帧）。在堆栈中存放好了数据后就可以进入被调用的函数。在完成被调用函数之后，他会弹出堆栈顶部元素，以恢复在进行函数调用之前所在的函数。在进行回文检查之前，递归函数将在堆栈中创建 n 个堆栈帧，计算机会逐个弹出进行处理。所以在使用递归时空间复杂度要考虑堆栈的使用情况。

排序

14 数组中重复的数字

问题描述

在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的，但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如，如果输入长度为7的数组[2,3,1,0,2,5,3]，那么对应的输出是2或者3。存在不合法的输入的话输出-1

实例

输入：[2,3,1,0,2,5,3]

返回值：2

说明：2或3都是对的

方案一：位置重排（推荐使用）

思路

既然数组长度为nnn只包含了0到n−1n-1n−1的数字，那么如果数字没有重复，这些数字排序后将会与其下标一一对应。那我们就可以考虑遍历数组，每次检查数字与下标是不是一致的，一致的说明它在属于它的位置上，不一致我们就将其交换到该数字作为下标的位置上，如果交换过程中，那个位置已经出现了等于它下标的数字，那肯定就重复了

具体做法

• 遍历数组，遇到数组元素与下标相同的不用管
• 遇到数组元素与下标不同，就将其交换到属于它的位置，交换前检查那个位置是否有相同的元素，若有则重复。
• 没有重复数据，返回-1

图示

代码实现

import java.util.*;
public class Solution {
    //交换函数
    private void swap(int[] numbers, int a, int b){
        int temp = numbers[a];
        numbers[a] = numbers[b];
        numbers[b] = temp;
    }
    public int duplicate (int[] numbers) {
        for(int i = 0; i < numbers.length; i++){
            //该位置本来就是对的
            if(numbers[i] == i)
                continue;
            //位置不对，需要换到自己对应的位置
            else{
                //对应位置相等，重复
                if(numbers[i] == numbers[numbers[i]])
                    return numbers[i];
                //交换位置
                else
                    swap(numbers, i, numbers[i]);
            }
        }
        //没有重复
        return -1;
    }
}
    

方案二：hash表

哈希表是一种根据关键码（key）直接访问值（value）的一种数据结构。而这种直接访问意味着只要知道key就能在O(1)时间内得到value，因此哈希表常用来统计频率、快速检验某个元素是否出现过等。

分析

既然是找重复的问题，那我们利用哈希表记录频率也是一样可以的。只要遇到的元素在哈希表中出现过，它就重复了。

步骤

• 遍历数组，将没有出现过的元素加入哈希表
• 遇到的元素在哈希表中出现过就是重复数组
• 遍历结束也没找到就返回-1

代码实现

import java.util.*;
public class Solution {
    public int duplicate (int[] numbers) {
        //哈希表记录重复
        HashMap<Integer, Integer> mp = new HashMap<>();
        //遍历数组
        for(int i = 0; i < numbers.length; i++){
            //如果没有出现过就加入哈希表
            if(!mp.containsKey(numbers[i]))
                mp.put(numbers[i], 1);
            //否则就是重复数字
            else
                return numbers[i];
        }
        //没有重复
        return -1;
    }
}

复杂度分析

• 时间复杂度：O(n)，其中n为数组长度，遍历一次数组，哈希表每次操作都是O(1)
• 空间复杂度：O(n)，哈希表最大的空间为数组长度

15 数组中的逆序对

方案一：归并排序(推荐使用)

描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P mod 1000000007

要求

实例说明

输入：[1,2,3,4,5,6,7,0]
返回值：7

输入：[1,2,3]
返回值：0

分析

题目主要信息

• 在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。
• 输入一个数组，求一个数组的全部逆序对，答案对1000000007取模
• 保证输入的数组中没有的相同的数字

知识点：分治

分治即“分而治之”，“分”指的是将一个大而复杂的问题划分成多个性质相同但是规模更小的子问题，子问题继续按照这样划分，直到问题可以被轻易解决；“治”指的是将子问题单独进行处理。经过分治后的子问题，需要将解进行合并才能得到原问题的解，因此整个分治过程经常用递归来实现。

思路

因为我们在归并排序过程中会将数组划分成最小为1个元素的子数组，然后依次比较子数组的每个元素的大小，依次取出较小的一个合并成大的子数组。

//取中间
int mid = (left + right) / 2; 
//左右划分合并
merge(divide(left, mid, data, temp), divide(mid + 1, right, data, temp)); 

这里我们也可以用相同的方法划分，划分之后相邻一个元素的子数组就可以根据大小统计逆序对，而不断往上合并的时候，因为已经排好序了，我们逆序对可以往上累计。我们主要有以下三个阶段。

具体做法

• step 1： 划分阶段：将待划分区间从中点划分成两部分，两部分进入递归继续划分，直到子数组长度为1.
• step 2： 排序阶段：使用归并排序递归地处理子序列，同时统计逆序对，因为在归并排序中，我们会依次比较相邻两组子数组各个元素的大小，并累计遇到的逆序情况。而对排好序的两组，右边大于左边时，它大于了左边的所有子序列，基于这个性质我们可以不用每次加1来统计，减少运算次数。
• step 3： 合并阶段：将排好序的子序列合并，同时累加逆序对。

图示

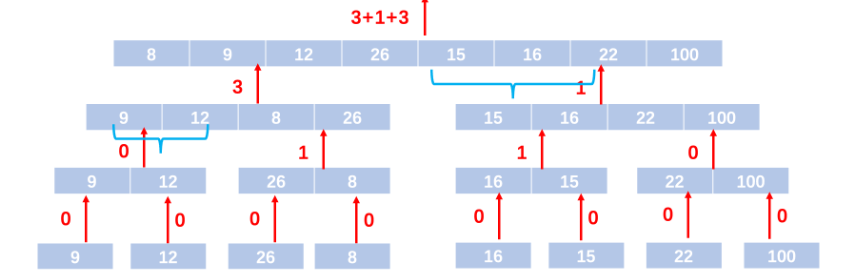
代码

package com.geekmice.onetomany.sf;

public class JZ51 {
    public static void main(String[] args) {
        JZ51 jz51 = new JZ51();
        int[] temp = new int[]{1, 2, 3, 4, 5, 6, 7, 0};
        int p = jz51.InversePairs(temp);
        System.out.println(p); // 7
    }
    public int mod = 1000000007;

    public int mergeSort(int left, int right, int[] data, int[] temp) {
        //停止划分
        if (left >= right)
            return 0;
        //取中间
        int mid = (left + right) / 2;
        //左右划分合并
        int res = mergeSort(left, mid, data, temp) + mergeSort(mid + 1, right, data, temp);
        //防止溢出
        res %= mod;
        int i = left, j = mid + 1;
        for (int k = left; k <= right; k++) {
            temp[k] = data[k];
        }
        for (int k = left; k <= right; k++) {
            if (i == mid + 1) {
                data[k] = temp[j++];
            } else if (j == right + 1 || temp[i] <= temp[j]) {
                data[k] = temp[i++];
                //左边比右边大，答案增加
            } else {
                data[k] = temp[j++];
                // 统计逆序对
                res += mid - i + 1;
            }
        }
        return res % mod;
    }

    public int InversePairs(int[] array) {
        int n = array.length;
        int[] res = new int[n];
        return mergeSort(0, n - 1, array, res);
    }

}

时间复杂度

方案二：树状数组（扩展思路）

思路

我们在统计逆序的时候，使用方法一的归并思想，就是利用排序好的部分直接获取逆序个数，而不是一个一个地比较，这样就像是把前面逆序对的个数累加起来，与前缀和类似。

而树状数组是如图所示的数组，它正好可以累加前缀和。

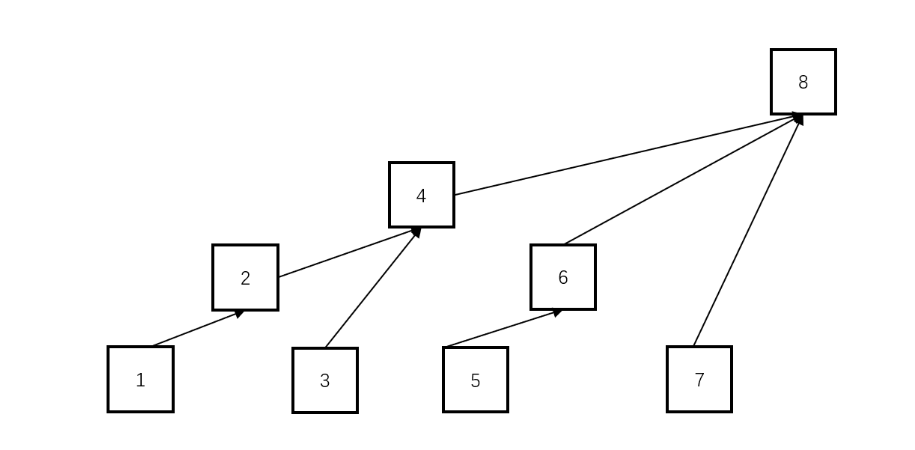
具体做法

• step 1：首先利用一个辅助数组，复制原数组然后排序，得到一个有序序列。
• step 2：然后对原数组进行离散化操作，利用二分查找映射，将数字变成其在有序数组中的位置，即数组[1 5000 2 400 30] 映射为 ——> [1 5 2 4 3]，这样我们能根据这个数字在有序数组中的位置和实际位置判断它前面有多少是逆序的，同时不必开辟数字原本大小的空间，减少空间需求。因为题目所给没有重复元素，因此也不用去重，还是nnn个数字。
• step 3：然后从前往后遍历每个元素，查找在树状数组中的前缀和，表示这个元素在树状数组中出现过多少，前缀和做差，表示值在[array[i]+1,n][array[i]+1,n][array[i]+1,n]中出现的次数，也就是逆序数个数。

代码实现

import java.util.*;
class BIT {
    private int[] tree;
    private int n;
    //初始化树状数组的大小
    public BIT(int m) { 
        this.n = m;
        this.tree = new int[m + 1];
    }
    //使数组呈现2、4、8、16这种树状
    public int lowbit(int x) { 
        return x & (-x);
    }
    //查询序列1到x的前缀和
    public int query(int x) { 
        int res = 0;
        while(x != 0){
            res += tree[x];
            x -= lowbit(x);
        }
        return res;
    }
    //序列x位置的数加1
    public void update(int x) { 
        while(x <= n){
            tree[x]++;
            x += lowbit(x);
        }
    }
}

public class Solution {
    public int mod = 1000000007;
    public int InversePairs(int [] array) {
        int n = array.length;
        int[] temp = new int[n];
        System.arraycopy(array, 0, temp, 0, n);
        //排序得到一份有序的数组
        Arrays.sort(temp); 
        //二分法重新映射，将数字变成其在有序数组中的位置
        for (int i = 0; i < n; ++i) 
            //二分法查找在其在有序数组中的位置
            array[i] = Arrays.binarySearch(temp, array[i]) + 1;
        //建立大小为n的树状数组
        BIT bit = new BIT(n); 
        int res = 0;
        //统计逆序对
        for(int i = 0; i < n; i++){ 
            //前缀和做差
            res = (res + bit.query(n) - bit.query(array[i])) % mod;
            bit.update(array[i]);
        }
        return res;
    }
}

时间复杂度

16 最小的K个数

方法一：堆排序（推荐使用）

知识点：优先队列

优先队列即PriorityQueue，是一种内置的机遇堆排序的容器，分为大顶堆与小顶堆，大顶堆的堆顶为最大元素，其余更小的元素在堆下方，小顶堆与其刚好相反。且因为容器内部的次序基于堆排序，因此每次插入元素时间复杂度都是O(log2n)O(log_2n)O(log2n)，而每次取出堆顶元素都是直接取出。

思路：

要找到最小的k个元素，只需要准备k个数字，之后每次遇到一个数字能够快速的与这k个数字中最大的值比较，每次将最大的值替换掉，那么最后剩余的就是k个最小的数字了。

如何快速比较k个数字的最大值，并每次替换成较小的新数字呢？我们可以考虑使用优先队列（大根堆），只要限制堆的大小为k，那么堆顶就是k个数字的中最大值，如果需要替换，将这个最大值拿出，加入新的元素就好了。

具体做法：

• step 1：利用input数组中前k个元素，构建一个大小为k的大顶堆，堆顶为这k个元素的最大值。
• step 2：对于后续的元素，依次比较其与堆顶的大小，若是比堆顶小，则堆顶弹出，再将新数加入堆中，直至数组结束，保证堆中的k个最小。
• step 3：最后将堆顶依次弹出即是最小的k个数。

import java.util.*;
public class Solution {
    public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) {
        ArrayList<Integer> res = new ArrayList<Integer>();
        //排除特殊情况
        if(k == 0 || input.length == 0) 
            return res;
        //大根堆 
        PriorityQueue<Integer> q = new PriorityQueue<>((o1, o2)->o2.compareTo(o1));
        //构建一个k个大小的堆  
        for(int i = 0; i < k; i++)
            q.offer(input[i]);
        for(int i = k; i < input.length; i++){
            //较小元素入堆
            if(q.peek() > input[i]){  
                q.poll();
                q.offer(input[i]);
            }
        }
        //堆中元素取出入数组
        for(int i = 0; i < k; i++) 
            res.add(q.poll());
        return res;
    }
}

方法二：sort排序法（扩展思路）

思路：

当然，如果这个数组本来就是有序的（递增序），那最小的k个数字，是不是就是数组前k个呢？那我们只要对整个数组进行了一次排序，那最小的k个元素不就手到擒来了。

具体做法：

• step 1：优先判断k为0或者输入数组长度为0的特殊情况。
• step 2：使用sort函数对整个数组排序。
• step 3：遍历排序后的数组前k个元素即可获取最小的k个。

import java.util.*;
public class Solution {
    public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) {
        ArrayList<Integer> res = new ArrayList<Integer>();
        //排除特殊情况
        if(k == 0 || input.length == 0) 
            return res;
        //排序
        Arrays.sort(input); 
        //因为k<=input.length,取前k小
        for(int i = 0; i < k; i++){ 
            res.add(input[i]);
        }
        return res;
    }
}

17 数据流中的中位数

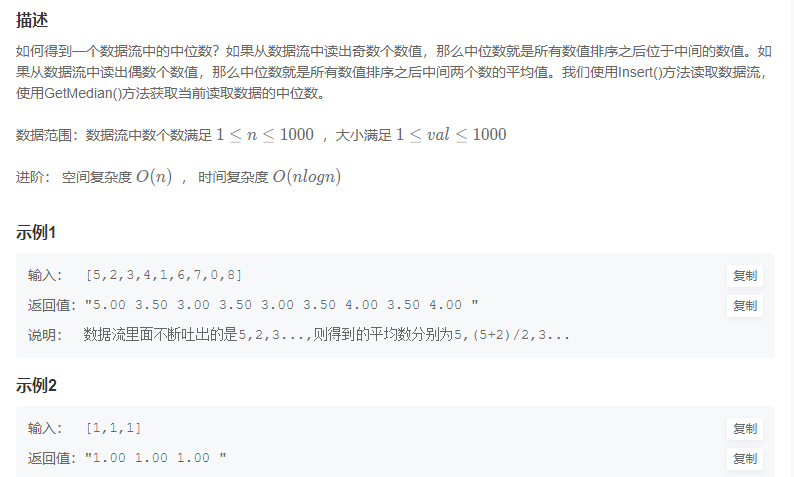
方法一：插入排序法（推荐使用）

知识点：插入排序

插入排序是排序中的一种方式，一旦一个无序数组开始排序，它前面部分就是已经排好的有序数组（一开始长度为0），而其后半部分则是需要排序的无序数组，插入排序的做法就是遍历后续需要排序的无序部分，对于每个元素，插入到前半部分有序数组中属于它的位置——即最后一个小于它的元素后。

思路：

传统的寻找中位数的方法便是排序之后，取中间值或者中间两位的平均即可。但是这道题因为数组在不断增长，每增长一位便需要排一次，很浪费时间，于是可以考虑在增加数据的同时将其有序化，这个过程就让我们想到了插入排序：对于每个输入的元素，遍历已经有序的数组，将其插入到属于它的位置。

具体做法：

• step 1：用一数组存储输入的数据流。
• step 2：Insert函数在插入的同时，遍历之前存储在数组中的数据，按照递增顺序依次插入，如此一来，加入的数据流便是有序的。
• step 3：GetMedian函数可以根据下标直接访问中位数，分为数组为奇数个元素和偶数个元素两种情况。记得需要类型转换为double。

import java.util.*;
public class Solution {
    private ArrayList<Integer> val = new ArrayList<Integer>();
    public void Insert(Integer num) {
        if(val.isEmpty())
            //val中没有数据，直接加入
            val.add(num); 
        //val中有数据，需要插入排序
        else{ 
            int i = 0;
            //遍历找到插入点
            for(; i < val.size(); i++){
                if(num <= val.get(i))
                   break;
            }
            //插入相应位置
            val.add (i, num); 
        }
    }

    public Double GetMedian() {
        int n = val.size();
        //奇数个数字
        if(n % 2 == 1) 
            //类型转换
            return (double)val.get(n / 2); 
        //偶数个数字
        else{ 
            double a = val.get(n / 2);
            double b = val.get(n / 2 - 1);
            return (a + b) / 2;
        }
    }
}

方法二：堆排序（扩展思路）

知识点：优先队列

优先队列即PriorityQueue，是一种内置的机遇堆排序的容器，分为大顶堆与小顶堆，大顶堆的堆顶为最大元素，其余更小的元素在堆下方，小顶堆与其刚好相反。且因为容器内部的次序基于堆排序，因此每次插入元素时间复杂度都是O(log2n)O(log_2n)O(log2n)，而每次取出堆顶元素都是直接取出。

思路：

除了插入排序，我们换种思路，因为插入排序每次要遍历整个已经有的数组，很浪费时间，有没有什么可以找到插入位置时能够更方便。

我们来看看中位数的特征，它是数组中间个数字或者两个数字的均值，它是数组较小的一半元素中最大的一个，同时也是数组较大的一半元素中最小的一个。那我们只要每次维护最小的一半元素和最大的一半元素，并能快速得到它们的最大值和最小值，那不就可以了嘛。这时候就可以想到了堆排序的优先队列。

具体做法：

• step 1：我们可以维护两个堆，分别是大顶堆min，用于存储较小的值，其中顶部最大；小顶堆max，用于存储较大的值，其中顶部最小，则中位数只会在两个堆的堆顶出现。
• step 2：我们可以约定奇数个元素时取大顶堆的顶部值，偶数个元素时取两堆顶的平均值，则可以发现两个堆的数据长度要么是相等的，要么奇数时大顶堆会多一个。
• step 3：每次输入的数据流先进入大顶堆排序，然后将大顶堆的最大值弹入小顶堆中，完成整个的排序。
• step 4：但是因为大顶堆的数据不可能会比小顶堆少一个，因此需要再比较二者的长度，若是小顶堆长度小于大顶堆，需要从大顶堆中弹出最小值到大顶堆中进行平衡。

import java.util.*;
public class Solution {
    //小顶堆，元素数值都比大顶堆大
    private PriorityQueue<Integer> max = new PriorityQueue<>();
    //大顶堆，元素数值较小 
    private PriorityQueue<Integer> min = new PriorityQueue<>((o1, o2)->o2.compareTo(o1)); 
    //维护两个堆，取两个堆顶部即与中位数相关
    public void Insert(Integer num) {
        //先加入较小部分
        min.offer(num);
        //将较小部分的最大值取出，送入到较大部分
        max.offer(min.poll());  
        //平衡两个堆的数量
        if(min.size() < max.size())  
            min.offer(max.poll());
    }

    public Double GetMedian() {
        //奇数个
        if(min.size() > max.size()) 
            return (double)min.peek();
        else
            //偶数个
            return (double)(min.peek() + max.peek()) / 2; 
    }

}

P5 冒泡排序（BubbleSort）

介绍情况

冒泡排序 是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

• 步骤1: 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
• 步骤2: 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
• 步骤3: 针对所有的元素重复以上的步骤，除了最后一个；
• 步骤4: 重复步骤1~3，直到排序完成。

代码实现

/**
     * 冒泡排序
     * 每轮循环将最大值放到最后一个位置
     * @param array
     * @return
     */
    public static int[] bubbleSort(int[] array) {
        if (array.length == 0)
            return array;
        for (int i = 0; i < array.length; i++)
            for (int j = 0; j < array.length - 1 - i; j++)
                if (array[j + 1] < array[j]) {
                    int temp = array[j + 1];
                    array[j + 1] = array[j];
                    array[j] = temp;
                }
        return array;
    }

算法分析

• 最佳情况：T(n) = O(n)
• 最差情况：T(n) = O(n2)
• 平均情况：T(n) = O(n2)

18 选择排序

介绍情况

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

代码实现

 /**
     * 选择排序
     * @param array
     * @return
     */
    public static int[] selectionSort(int[] array) {
        if (array.length == 0)
            return array;
        for (int i = 0; i < array.length; i++) {
            int minIndex = i;
            for (int j = i; j < array.length; j++) {
                if (array[j] < array[minIndex]) //找到最小的数
                    minIndex = j; //将最小数的索引保存
            }
            int temp = array[minIndex];
            array[minIndex] = array[i];
            array[i] = temp;
        }
        return array;
    }

算法分析

• 最佳情况：T(n) = O(n^2)
• 最差情况：T(n) = O(n^2)
• 平均情况：T(n) = O(n^2)

19 插入排序

简要概述

有序区，无序区划分，默认第一个元素有序区，其他元素无序区，每次从无序区选择一个元素
去和有序区元素比较，从后往前依次比较，数据覆盖

一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：
步骤1: 从第一个元素开始，该元素可以认为已经被排序；
步骤2: 取出下一个元素，在已经排序的元素序列中从后向前扫描；
步骤3: 如果该元素（已排序）大于新元素，将该元素移到下一位置；
步骤4: 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
步骤5: 将新元素插入到该位置后；
步骤6: 重复步骤2~5。

代码实现

   /**
     * 插入排序
     * @param array
     * @return
     */
    public static int[] insertionSort(int[] array) {
        if (array.length == 0){
            return array;
        }
        // 有序区 第一个元素
        // 无序区 除了第一个之外所有元素
        for(int i=1;i<array.length-1;i++){
            // 取出要插入元素
            int temp=array[i];
            // 取出数据下标
            int j=i;
            // 待插入元素和有序区比较
            while(j>0&&temp < array[i-1]){
                array[j]=array[j-1];
                j--;
            }
            // 覆盖数据
            array[j]=temp;
        }
        return array;
    }

算法分析

• 最佳情况：T(n) = O(n)
• 最坏情况：T(n) = O(n2)
• 平均情况：T(n) = O(n2)

20 希尔排序

简要概述

我们来看下希尔排序的基本步骤，在此我们选择增量gap=length/2，缩小增量继续以gap = gap/2的方式，这种增量选择我们可以用一个序列来表示，{n/2,(n/2)/2…1}，称为增量序列。希尔排序的增量序列的选择与证明是个数学难题，我们选择的这个增量序列是比较常用的，也是希尔建议的增量，称为希尔增量，但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。

先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述：
步骤1：选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
步骤2：按增量序列个数k，对序列进行k 趟排序；
步骤3：每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

代码实现

/**
     * 希尔排序
     *
     * @param array
     * @return
     */
    public static int[] ShellSort(int[] array) {
        int len = array.length;
        int temp, gap = len / 2;
        while (gap > 0) {
            for (int i = gap; i < len; i++) {
                temp = array[i];
                int preIndex = i - gap;
                while (preIndex >= 0 && array[preIndex] > temp) {
                    array[preIndex + gap] = array[preIndex];
                    preIndex -= gap;
                }
                array[preIndex + gap] = temp;
            }
            gap /= 2;
        }
        return array;
    }

算法分析

• 最佳情况：T(n) = O(nlog2 n)
• 最坏情况：T(n) = O(nlog2 n)
• 平均情况：T(n) =O(nlog2n)

21 归并排序

简要概述

和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是O(n log n）的时间复杂度。代价是需要额外的内存空间。

归并排序 是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。
步骤1：把长度为n的输入序列分成两个长度为n/2的子序列；
步骤2：对这两个子序列分别采用归并排序；
步骤3：将两个排序好的子序列合并成一个最终的排序序列。

代码实现

/**
     * 归并排序
     *
     * @param array
     * @return
     */
    public static int[] MergeSort(int[] array) {
        if (array.length < 2) return array;
        int mid = array.length / 2;
        int[] left = Arrays.copyOfRange(array, 0, mid);
        int[] right = Arrays.copyOfRange(array, mid, array.length);
        return merge(MergeSort(left), MergeSort(right));
    }
    /**
     * 归并排序——将两段排序好的数组结合成一个排序数组
     *
     * @param left
     * @param right
     * @return
     */
    public static int[] merge(int[] left, int[] right) {
        int[] result = new int[left.length + right.length];
        for (int index = 0, i = 0, j = 0; index < result.length; index++) {
            if (i >= left.length)
                result[index] = right[j++];
            else if (j >= right.length)
                result[index] = left[i++];
            else if (left[i] > right[j])
                result[index] = right[j++];
            else
                result[index] = left[i++];
        }
        return result;
    }

算法分析

• 最佳情况：T(n) = O(n)
• 最差情况：T(n) = O(nlogn)
• 平均情况：T(n) = O(nlogn)

22 快速排序

简要概述

通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序

快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：
步骤1：从数列中挑出一个元素，称为 “基准”（pivot ）；
步骤2：重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
步骤3：递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

代码实现

/**
     * 快速排序方法
     * @param array
     * @param start
     * @param end
     * @return
     */
    public static int[] QuickSort(int[] array, int start, int end) {
        if (array.length < 1 || start < 0 || end >= array.length || start > end) return null;
        int smallIndex = partition(array, start, end);
        if (smallIndex > start)
            QuickSort(array, start, smallIndex - 1);
        if (smallIndex < end)
            QuickSort(array, smallIndex + 1, end);
        return array;
    }
    /**
     * 快速排序算法——partition
     * @param array
     * @param start
     * @param end
     * @return
     */
    public static int partition(int[] array, int start, int end) {
        int pivot = (int) (start + Math.random() * (end - start + 1));
        int smallIndex = start - 1;
        swap(array, pivot, end);
        for (int i = start; i <= end; i++)
            if (array[i] <= array[end]) {
                smallIndex++;
                if (i > smallIndex)
                    swap(array, i, smallIndex);
            }
        return smallIndex;
    }
 
    /**
     * 交换数组内两个元素
     * @param array
     * @param i
     * @param j
     */
    public static void swap(int[] array, int i, int j) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }

算法分析

• 最佳情况：T(n) = O(nlogn)
• 最差情况：T(n) = O(n2)
• 平均情况：T(n) = O(nlogn)

24 堆排序

简要概述

堆排序（Heapsort） 是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。
步骤1：将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区；
步骤2：将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；
步骤3：由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

代码实现

//声明全局变量，用于记录数组array的长度；
    static int len;
    /**
     * 堆排序算法
     *
     * @param array
     * @return
     */
    public static int[] HeapSort(int[] array) {
        len = array.length;
        if (len < 1) return array;
        //1.构建一个最大堆
        buildMaxHeap(array);
        //2.循环将堆首位（最大值）与末位交换，然后在重新调整最大堆
        while (len > 0) {
            swap(array, 0, len - 1);
            len--;
            adjustHeap(array, 0);
        }
        return array;
    }
    /**
     * 建立最大堆
     *
     * @param array
     */
    public static void buildMaxHeap(int[] array) {
        //从最后一个非叶子节点开始向上构造最大堆
        //for循环这样写会更好一点：i的左子树和右子树分别2i+1和2(i+1)
        for (int i = (len/2- 1); i >= 0; i--) {
            adjustHeap(array, i);
        }
    }
    /**
     * 调整使之成为最大堆
     *
     * @param array
     * @param i
     */
    public static void adjustHeap(int[] array, int i) {
        int maxIndex = i;
        //如果有左子树，且左子树大于父节点，则将最大指针指向左子树
        if (i * 2 < len && array[i * 2] > array[maxIndex])
            maxIndex = i * 2 + 1;
        //如果有右子树，且右子树大于父节点，则将最大指针指向右子树
        if (i * 2 + 1 < len && array[i * 2 + 1] > array[maxIndex])
            maxIndex = i * 2 + 2; 
        //如果父节点不是最大值，则将父节点与最大值交换，并且递归调整与父节点交换的位置。
        if (maxIndex != i) {
            swap(array, maxIndex, i);
            adjustHeap(array, maxIndex);
        }
    }

算法分析

• 最佳情况：T(n) = O(nlogn)
• 最差情况：T(n) = O(nlogn)
• 平均情况：T(n) = O(nlogn)

25 计数排序

简要概述

计数排序 的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

计数排序(Counting sort) 是一种稳定的排序算法。计数排序使用一个额外的数组C，其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。

8.1 算法描述
步骤1：找出待排序的数组中最大和最小的元素；
步骤2：统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
步骤3：对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
步骤4：反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

代码实现

    /**
     * 计数排序
     *
     * @param array
     * @return
     */
    public static int[] CountingSort(int[] array) {
        if (array.length == 0) return array;
        int bias, min = array[0], max = array[0];
        for (int i = 1; i < array.length; i++) {
            if (array[i] > max)
                max = array[i];
            if (array[i] < min)
                min = array[i];
        }
        bias = 0 - min;
        int[] bucket = new int[max - min + 1];
        Arrays.fill(bucket, 0);
        for (int i = 0; i < array.length; i++) {
            bucket[array[i] + bias]++;
        }
        int index = 0, i = 0;
        while (index < array.length) {
            if (bucket[i] != 0) {
                array[index] = i - bias;
                bucket[i]--;
                index++;
            } else
                i++;
        }
        return array;
    }

算法分析

当输入的元素是n 个0到k之间的整数时，它的运行时间是 O(n + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法。由于用来计数的数组C的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存。

最佳情况：T(n) = O(n+k)
最差情况：T(n) = O(n+k)
平均情况：T(n) = O(n+k)

27 桶排序

简要概述

桶排序 是计数排序的升级版，将数据分到有限数量的桶子里，然后每个桶再分别排序

桶排序 (Bucket sort)的工作的原理：

代码实现

package com.geekmice.arithmetic;

import java.util.ArrayList;

public class BucketSortTest {

    public static void main(String[] args) {
        ArrayList<Integer> array = new ArrayList<>();
        array.add(1);
        array.add(-1);
        array.add(9);
        array.add(3);
        array.add(3);
        array.add(7);
        array.add(0);
        array.add(11);
        ArrayList<Integer> result = bucketSort(array, 3);
        System.out.println(result);
    }


    /**
     * 桶排序
     * @param array
     * @param bucketSize
     * @return
     */
    public static ArrayList<Integer> bucketSort(ArrayList<Integer> array, int bucketSize) {
        if (array == null || array.size() < 2) {
            return array;
        }
        int max = array.get(0), min = array.get(0);
        // 找到最大值最小值
        for (int i = 0; i < array.size(); i++) {
            if (array.get(i) > max) {
                max = array.get(i);
            }
            if (array.get(i) < min) {
                min = array.get(i);
            }
        }
        int bucketCount = (max - min) / bucketSize + 1;
        ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketCount);
        ArrayList<Integer> resultArr = new ArrayList<>();
        for (int i = 0; i < bucketCount; i++) {
            bucketArr.add(new ArrayList<Integer>());
        }
        for (int i = 0; i < array.size(); i++) {
            bucketArr.get((array.get(i) - min) / bucketSize).add(array.get(i));
        }
        for (int i = 0; i < bucketCount; i++) {
            if (bucketSize == 1) { // 如果带排序数组中有重复数字时
                for (int j = 0; j < bucketArr.get(i).size(); j++)
                    resultArr.add(bucketArr.get(i).get(j));
            } else {
                if (bucketCount == 1) {
                    bucketSize--;
                }
                ArrayList<Integer> temp = bucketSort(bucketArr.get(i), bucketSize);
                for (int j = 0; j < temp.size(); j++) {
                    resultArr.add(temp.get(j));
                }
            }
        }
        return resultArr;
    }
}

[-1, 0, 1, 3, 3, 7, 9, 11]

算法分析

1.时间复杂度
桶排序算法遍历了2次原始数组，运算量为2N，最后，遍历桶输出排序结果的运算量为N，初始化桶的运算量为M。

对桶进行排序，不同的排序算法算法复杂度不同，冒泡排序算法复杂度为O(N^2)，堆排序、归并排序算法复杂度为O(NlogN)，我们以排序算法复杂度为O(NlogN)进行计算，运算量为N/M*log(N/M)*M

最终的运算量为3N+M+N/M*log(N/M)*M，即3N+M+N(logN-logM)，去掉系数，时间复杂度为O(N+M+N(logN-logM))

2.空间复杂度
桶排序算法排序过程中新建了一个桶和一个输出数组，所以算法的空间复杂度是O(N+M)

3.稳定性
桶排序算法在对每个桶进行排序时，选择稳定的排序算法，则排序后，相同元素的位置不会发生改变，所以桶排序算法是一种稳定的排序算法

28 基数排序

简要概述

基数排序也是非比较的排序算法，对每一位进行排序，从最低位开始排序，复杂度为O(kn),为数组长度，k为数组中的数的最大的位数；

基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。基数排序基于分别排序，分别收集，所以是稳定的。
步骤1：取得数组中的最大数，并取得位数；
步骤2：arr为原始数组，从最低位开始取每个位组成radix数组；
步骤3：对radix进行计数排序（利用计数排序适用于小范围数的特点）；

代码实现

    /**
     * 基数排序
     *
     * @param array
     * @return
     */
    public static int[] RadixSort(int[] array) {
        if (array == null || array.length < 2) {
            return array;
        }
        // 1.先算出最大数的位数；
        int max = array[0];
        for (int i = 1; i < array.length; i++) {
            max = Math.max(max, array[i]);
        }
        int maxDigit = 0;
        while (max != 0) {
            max /= 10;
            maxDigit++;
        }
        int mod = 10, div = 1;
        ArrayList<ArrayList<Integer>> bucketList = new ArrayList<ArrayList<Integer>>();
        for (int i = 0; i < 10; i++)
            bucketList.add(new ArrayList<Integer>());
        for (int i = 0; i < maxDigit; i++, mod *= 10, div *= 10) {
            for (int j = 0; j < array.length; j++) {
                int num = (array[j] % mod) / div;
                bucketList.get(num).add(array[j]);
            }
            int index = 0;
            for (int j = 0; j < bucketList.size(); j++) {
                for (int k = 0; k < bucketList.get(j).size(); k++) {
                    array[index++] = bucketList.get(j).get(k);
                }
                bucketList.get(j).clear();
            }
        }
        return array;
    }

算法分析

• • 最佳情况：T(n) = O(n * k)
  • 最差情况：T(n) = O(n * k)
  • 平均情况：T(n) = O(n * k)
• 基数排序有两种方法：
  • MSD 从高位开始进行排序
  • LSD 从低位开始进行排序

这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

• 基数排序： 根据键值的每位数字来分配桶
• 计数排序： 每个桶只存储单一键值
• 桶排序： 每个桶存储一定范围的数值

数组

在处理数组和链表相关问题时，双指针技巧是经常用到的，双指针技巧主要分为两类：左右指针和快慢指针。

所谓左右指针，就是两个指针相向而行或者相背而行；而所谓快慢指针，就是两个指针同向而行，一快一慢。

对于单链表来说，大部分技巧都属于快慢指针，比如链表环判断，倒数第 K 个链表节点等问题，它们都是通过一个 fast 快指针和一个 slow 慢指针配合完成任务。

在数组中并没有真正意义上的指针，但我们可以把索引当做数组中的指针，这样也可以在数组中施展双指针技巧

29 两数之和-输入有序数组

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

示例 1：

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

示例 2：

输入：numbers = [2,3,4], target = 6
输出：[1,3]
解释：2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。

示例 3：

输入：numbers = [-1,0], target = -1
输出：[1,2]
解释：-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

方法一：双指针

思路

初始时两个指针分别指向第一个元素位置和最后一个元素的位置。每次计算两个指针指向的两个元素之和，并和目标值比较。如果两个元素之和等于目标值，则发现了唯一解。如果两个元素之和小于目标值，则将左侧指针右移一位。如果两个元素之和大于目标值，则将右侧指针左移一位。移动指针之后，重复上述操作，直到找到答案。

代码实现

public int[] twoSum(int[] numbers, int target) {
    int i = 0;
    int j = numbers.length - 1;
    while (i < j) {
        int sum = numbers[i] + numbers[j];
        if (sum < target) {
            i++;
        } else if (sum > target) {
            j--;
        } else {
            return new int[]{i+1, j+1};
        }
    }
    return new int[]{-1, -1};
}

复杂度分析

时间复杂度：O(N)，其中N表示数组长度，两个指针移动总次数最多N次

空间复杂度：O(1)

方法二：二分查找

思路

在数组中找到两个数，使得它们的和等于目标值，可以首先固定第一个数，然后寻找第二个数，第二个数等于目标值减去第一个数的差。利用数组的有序性质，可以通过二分查找的方法寻找第二个数。为了避免重复寻找，在寻找第二个数时，只在第一个数的右侧寻找。

代码实现

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        for (int i = 0; i < numbers.length; ++i) {
            int low = i + 1, high = numbers.length - 1;
            while (low <= high) {
                int mid = (high - low) / 2 + low;
                if (numbers[mid] == target - numbers[i]) {
                    return new int[]{i + 1, mid + 1};
                } else if (numbers[mid] > target - numbers[i]) {
                    high = mid - 1;
                } else {
                    low = mid + 1;
                }
            }
        }
        return new int[]{-1, -1};
    }
}

复杂度分析

时间复杂度：O(nlogn)，其中n表示数组长度，需要遍历数组一次确定第一个数，时间复杂度是O(n)，寻找第二个数使用二分查找，时间复杂度O(loog n)，，总的时间复杂度O(n log n)

空间复杂度：O(1)

30 和为S的两个数字

输入一个递增排序的数组和一个数字s，在数组中查找两个数，使得它们的和正好是s。如果有多对数字的和等于s，则输出任意一对即可。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[2,7] 或者 [7,2]

示例 2：

输入：nums = [10,26,30,31,47,60], target = 40
输出：[10,30] 或者 [30,10]

限制：

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^6

方法一：双指针

思路

代码实现

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int i = 0, j = nums.length - 1;
        while(i < j) {
            int s = nums[i] + nums[j];
            if(s < target) i++;
            else if(s > target) j--;
            else return new int[] { nums[i], nums[j] };
        }
        return new int[0];
    }
}

复杂度分析

时间复杂度：O(n)，n为nums数组长度，双指针共同线性遍历整个数组

空间复杂度：O(1)，变量i,j使用常数大小额外空间

31 删除有序数组中的重复项

给你一个 升序排列 的数组 nums ，请你** 原地** 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。

由于在某些语言中不能改变数组的长度，所以必须将结果放在数组nums的第一部分。更规范地说，如果在删除重复项之后有 k 个元素，那么 nums 的前 k 个元素应该保存最终结果。

将最终结果插入 nums 的前 k 个位置后返回 k 。

不要使用额外的空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

方法一：双指针

思路

首先注意数组是有序的，那么重复的元素一定会相邻。

要求删除重复元素，实际上就是将不重复的元素移到数组的左侧。

考虑用 2 个指针，一个在前记作 p，一个在后记作 q，算法流程如下：

1.比较 p 和 q 位置的元素是否相等。

如果相等，q 后移 1 位 如果不相等，将 q 位置的元素复制到 p+1 位置上，p 后移一位，q 后移 1 位 重复上述过程，直到 q 等于数组长度。

返回 p + 1，即为新数组长度。

代码实现

 public int removeDuplicates(int[] nums) {
    if(nums == null || nums.length == 0) return 0;
    int p = 0;
    int q = 1;
    while(q < nums.length){
        if(nums[p] != nums[q]){
            nums[p + 1] = nums[q];
            p++;
        }
        q++;
    }
    return p + 1;
}

复杂度分析

时间复杂度：O(n)

空间复杂度：O(1)

方法二：通用方法

思路

设定变量 idx，指向待插入位置。idx 初始值为 0，目标数组为 []

首先我们先让第 1 位直接保留（性质 1）。idx 变为 1，目标数组为 [3]

继续往后遍历，能够保留的前提是与 idx 的前面 1 位元素不同（性质 2），因此我们会跳过剩余的 3，将第一个 4 追加进去。idx 变为 2，目标数组为 [3,4]

继续这个过程，跳过剩余的 4，将第一个 5 追加进去。idx 变为 3，目标数组为 [3,4,5]

当整个数组被扫描完，最终我们得到了目标数组 [3,4,5] 和 答案 idx 为 3。

代码实现

class Solution {
    public int removeDuplicates(int[] nums) {   
        return process(nums, 1);
    }
    int process(int[] nums, int k) {
        int idx = 0; 
        for (int x : nums) {
            if (idx < k || nums[idx - k] != x) nums[idx++] = x;
        }
        return idx;
    }
}

复杂度分析

时间复杂度：O(N)

空间复杂度：O(1)

32 移除数组元素

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3]
解释：函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。

方法一：双指针

思路

代码实现

class Solution {
    public int removeElement(int[] nums, int val) {
        int n = nums.length;
        int left = 0;
        for (int right = 0; right < n; right++) {
            if (nums[right] != val) {
                nums[left] = nums[right];
                left++;
            }
        }
        return left;
    }
}

复杂度分析

时间复杂度：O(n)，其中n 为序列的长度。我们只需要遍历该序列至多两次

空间复杂度：O(1)，我们只需要常数的空间保存若干变量

方法二：双指针优化

思路

代码实现

class Solution {
    public int removeElement(int[] nums, int val) {
        int left = 0;
        int right = nums.length;
        while (left < right) {
            if (nums[left] == val) {
                nums[left] = nums[right - 1];
                right--;
            } else {
                left++;
            }
        }
        return left;
    }
}

复杂度分析

时间复杂度：O(n)，其中 n 为序列的长度。我们只需要遍历该序列至多一次。

空间复杂度：O(1)，我们只需要常数的空间保存若干变量

33 移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

示例 2:

输入: nums = [0]
输出: [0]

方法一：双指针

思路

使用双指针，左指针指向当前已经处理好的序列的尾部，右指针指向待处理序列的头部。

右指针不断向右移动，每次右指针指向非零数，则将左右指针对应的数交换，同时左指针右移。

注意到以下性质：

左指针左边均为非零数；

右指针左边直到左指针处均为零。

因此每次交换，都是将左指针的零与右指针的非零数交换，且非零数的相对顺序并未改变。

代码实现

class Solution {
    public void moveZeroes(int[] nums) {
        int n = nums.length, left = 0, right = 0;
        while (right < n) {
            if (nums[right] != 0) {
                swap(nums, left, right);
                left++;
            }
            right++;
        }
    }

    public void swap(int[] nums, int left, int right) {
        int temp = nums[left];
        nums[left] = nums[right];	
        nums[right] = temp;
    }
}

复杂度分析

时间复杂度：O(n) 其中 n 为序列长度。每个位置至多被遍历两次

空间复杂度：O(1)

34 反转字符串

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。

不要给另外的数组分配额外的空间，你必须**原地修改输入数组**、使用 O(1) 的额外空间解决这一问题。

示例 1：

输入：s = ["h","e","l","l","o"]
输出：["o","l","l","e","h"]

示例 2：

输入：s = ["H","a","n","n","a","h"]
输出：["h","a","n","n","a","H"]

方法一：双指针

思路

对于长度为 N 的待被反转的字符数组，我们可以观察反转前后下标的变化，假设反转前字符数组为 s[0] s[1] s[2] … s[N - 1]，那么反转后字符数组为 s[N - 1] s[N - 2] … s[0]。比较反转前后下标变化很容易得出 s[i] 的字符与 s[N - 1 - i] 的字符发生了交换的规律，因此我们可以得出如下双指针的解法：

将 left 指向字符数组首元素，right 指向字符数组尾元素。
当 left < right：
交换 s[left] 和 s[right]；
left 指针右移一位，即 left = left + 1；
right 指针左移一位，即 right = right - 1。
当 left >= right，反转结束，返回字符数组即可。

代码实现

class Solution {
    public void reverseString(char[] s) {
        int n = s.length;
        for (int left = 0, right = n - 1; left < right; ++left, --right) {
            char tmp = s[left];
            s[left] = s[right];
            s[right] = tmp;
        }
    }
}

复杂度分析

时间复杂度：O(N) 其中 N 为字符数组的长度。一共执行了 N/2 次的交换

空间复杂度：O(1)

35 最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

提示：

• 1 <= s.length <= 1000
• s 仅由数字和英文字母组成

方法一：中心扩展算法

思路

代码实现

class Solution {
    public String longestPalindrome(String s) {
        if (s == null || s.length() < 1) {
            return "";
        }
        int start = 0, end = 0;
        for (int i = 0; i < s.length(); i++) {
            int len1 = expandAroundCenter(s, i, i);
            int len2 = expandAroundCenter(s, i, i + 1);
            int len = Math.max(len1, len2);
            if (len > end - start) {
                start = i - (len - 1) / 2;
                end = i + len / 2;
            }
        }
        return s.substring(start, end + 1);
    }

    public int expandAroundCenter(String s, int left, int right) {
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            --left;
            ++right;
        }
        return right - left - 1;
    }
}

复杂度分析

时间复杂度：O(N^2) 其中 nnn 是字符串的长度。长度为 1和 2 的回文中心分别有 n 和 n−1 个，每个回文中心最多会向外扩展 O(n) 次。

空间复杂度：O(1)

动态规划

36 编辑距离

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

想法

编辑距离算法被数据科学家广泛应用，是用作机器翻译和语音识别评价标准的基本算法。

最直观的方法是暴力检查所有可能的编辑方法，取最短的一个。所有可能的编辑方法达到指数级，但我们不需要进行这么多计算，因为我们只需要找到距离最短的序列而不是所有可能的序列。

方法一：动态规划

我们可以对任意一个单词进行三种操作：

插入一个字符；

删除一个字符；

替换一个字符。

题目给定了两个单词，设为 A 和 B，这样我们就能够六种操作方法。

但我们可以发现，如果我们有单词 A 和单词 B：

对单词 A 删除一个字符和对单词 B 插入一个字符是等价的。例如当单词 A 为 doge，单词 B 为 dog 时，我们既可以删除单词 A 的最后一个字符 e，得到相同的 dog，也可以在单词 B 末尾添加一个字符 e，得到相同的 doge；

同理，对单词 B 删除一个字符和对单词 A 插入一个字符也是等价的；

对单词 A 替换一个字符和对单词 B 替换一个字符是等价的。例如当单词 A 为 bat，单词 B 为 cat 时，我们修改单词 A 的第一个字母 b -> c，和修改单词 B 的第一个字母 c -> b 是等价的。

这样以来，本质不同的操作实际上只有三种：

在单词 A 中插入一个字符；

在单词 B 中插入一个字符；

修改单词 A 的一个字符。

这样以来，我们就可以把原问题转化为规模较小的子问题。我们用 A = horse，B = ros 作为例子，来看一看是如何把这个问题转化为规模较小的若干子问题的。

在单词 A 中插入一个字符：如果我们知道 horse 到 ro 的编辑距离为 a，那么显然 horse 到 ros 的编辑距离不会超过 a + 1。这是因为我们可以在 a 次操作后将 horse 和 ro 变为相同的字符串，只需要额外的 1 次操作，在单词 A 的末尾添加字符 s，就能在 a + 1 次操作后将 horse 和 ro 变为相同的字符串；

在单词 B 中插入一个字符：如果我们知道 hors 到 ros 的编辑距离为 b，那么显然 horse 到 ros 的编辑距离不会超过 b + 1，原因同上；

修改单词 A 的一个字符：如果我们知道 hors 到 ro 的编辑距离为 c，那么显然 horse 到 ros 的编辑距离不会超过 c + 1，原因同上。

那么从 horse 变成 ros 的编辑距离应该为 min(a + 1, b + 1, c + 1)。

注意：为什么我们总是在单词 A 和 B 的末尾插入或者修改字符，能不能在其它的地方进行操作呢？答案是可以的，但是我们知道，操作的顺序是不影响最终的结果的。例如对于单词 cat，我们希望在 c 和 a 之间添加字符 d 并且将字符 t 修改为字符 b，那么这两个操作无论为什么顺序，都会得到最终的结果 cdab。

你可能觉得 horse 到 ro 这个问题也很难解决。但是没关系，我们可以继续用上面的方法拆分这个问题，对于这个问题拆分出来的所有子问题，我们也可以继续拆分，直到：

字符串 A 为空，如从 转换到 ro，显然编辑距离为字符串 B 的长度，这里是 2；

字符串 B 为空，如从 horse 转换到 ，显然编辑距离为字符串 A 的长度，这里是 5。

因此，我们就可以使用动态规划来解决这个问题了。我们用 D[i][j] 表示 A 的前 i 个字母和 B 的前 j 个字母之间的编辑距离。

class Solution {
    public int minDistance(String word1, String word2) {
        int n = word1.length();
        int m = word2.length();

        // 有一个字符串为空串
        if (n * m == 0) {
            return n + m;
        }

        // DP 数组
        int[][] D = new int[n + 1][m + 1];

        // 边界状态初始化
        for (int i = 0; i < n + 1; i++) {
            D[i][0] = i;
        }
        for (int j = 0; j < m + 1; j++) {
            D[0][j] = j;
        }

        // 计算所有 DP 值
        for (int i = 1; i < n + 1; i++) {
            for (int j = 1; j < m + 1; j++) {
                int left = D[i - 1][j] + 1;
                int down = D[i][j - 1] + 1;
                int left_down = D[i - 1][j - 1];
                if (word1.charAt(i - 1) != word2.charAt(j - 1)) {
                    left_down += 1;
                }
                D[i][j] = Math.min(left, Math.min(down, left_down));
            }
        }
        return D[n][m];
    }
}

37 最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

方法一：动态规划

class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }
        int[] dp = new int[nums.length];
        dp[0] = 1;
        int maxans = 1;
        for (int i = 1; i < nums.length; i++) {
            dp[i] = 1;
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            maxans = Math.max(maxans, dp[i]);
        }
        return maxans;
    }
}

复杂度分析

方法二：贪心+二分查找

class Solution {
    public int lengthOfLIS(int[] nums) {
        int len = 1, n = nums.length;
        if (n == 0) {
            return 0;
        }
        int[] d = new int[n + 1];
        d[len] = nums[0];
        for (int i = 1; i < n; ++i) {
            if (nums[i] > d[len]) {
                d[++len] = nums[i];
            } else {
                int l = 1, r = len, pos = 0; // 如果找不到说明所有的数都比 nums[i] 大，此时要更新 d[1]，所以这里将 pos 设为 0
                while (l <= r) {
                    int mid = (l + r) >> 1;
                    if (d[mid] < nums[i]) {
                        pos = mid;
                        l = mid + 1;
                    } else {
                        r = mid - 1;
                    }
                }
                d[pos + 1] = nums[i];
            }
        }
        return len;
    }
}

复杂度分析

38 最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

方法一：动态规划

https://leetcode.cn/problems/maximum-subarray/solutions/9058/dong-tai-gui-hua-fen-zhi-fa-python-dai-ma-java-dai/

public class Solution {

    public int maxSubArray(int[] nums) {
        int len = nums.length;
        // dp[i] 表示：以 nums[i] 结尾的连续子数组的最大和
        int[] dp = new int[len];
        dp[0] = nums[0];

        for (int i = 1; i < len; i++) {
            if (dp[i - 1] > 0) {
                dp[i] = dp[i - 1] + nums[i];
            } else {
                dp[i] = nums[i];
            }
        }

        // 也可以在上面遍历的同时求出 res 的最大值，这里我们为了语义清晰分开写，大家可以自行选择
        int res = dp[0];
        for (int i = 1; i < len; i++) {
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

方法二：分治法

分治法的思路是这样的，其实也是分类讨论。

连续子序列的最大和主要由这三部分子区间里元素的最大和得到：

第 1 部分：子区间 [left, mid]；
第 2 部分：子区间 [mid + 1, right]；
第 3 部分：包含子区间 [mid , mid + 1] 的子区间，即 nums[mid] 与 nums[mid + 1] 一定会被选取。
对这三个部分求最大值即可。

public class Solution {

    public int maxSubArray(int[] nums) {
        int len = nums.length;
        if (len == 0) {
            return 0;
        }
        return maxSubArraySum(nums, 0, len - 1);
    }

    private int maxCrossingSum(int[] nums, int left, int mid, int right) {
        // 一定会包含 nums[mid] 这个元素
        int sum = 0;
        int leftSum = Integer.MIN_VALUE;
        // 左半边包含 nums[mid] 元素，最多可以到什么地方
        // 走到最边界，看看最值是什么
        // 计算以 mid 结尾的最大的子数组的和
        for (int i = mid; i >= left; i--) {
            sum += nums[i];
            if (sum > leftSum) {
                leftSum = sum;
            }
        }
        sum = 0;
        int rightSum = Integer.MIN_VALUE;
        // 右半边不包含 nums[mid] 元素，最多可以到什么地方
        // 计算以 mid+1 开始的最大的子数组的和
        for (int i = mid + 1; i <= right; i++) {
            sum += nums[i];
            if (sum > rightSum) {
                rightSum = sum;
            }
        }
        return leftSum + rightSum;
    }

    private int maxSubArraySum(int[] nums, int left, int right) {
        if (left == right) {
            return nums[left];
        }
        int mid = left + (right - left) / 2;
        return max3(maxSubArraySum(nums, left, mid),
                maxSubArraySum(nums, mid + 1, right),
                maxCrossingSum(nums, left, mid, right));
    }

    private int max3(int num1, int num2, int num3) {
        return Math.max(num1, Math.max(num2, num3));
    }
}

39 最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

• 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。

示例 2：

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。

示例 3：

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0 。

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int m = text1.length(), n = text2.length();
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            char c1 = text1.charAt(i - 1);
            for (int j = 1; j <= n; j++) {
                char c2 = text2.charAt(j - 1);
                if (c1 == c2) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[m][n];
    }
}

40 分割等和子集

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

提示：

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 100

我们能想到的，例如基于贪心算法的「将数组降序排序后，依次将每个元素添加至当前元素和较小的子集中」之类的方法都是错误的，可以轻松地举出反例。因此，我们必须尝试非多项式时间复杂度的算法，例如时间复杂度与元素大小相关的动态规划。

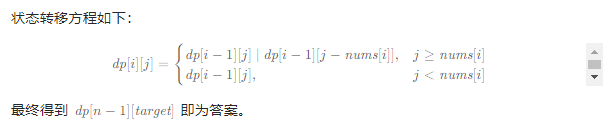
方法：动态规划

class Solution {
    public boolean canPartition(int[] nums) {
        int n = nums.length;
        if (n < 2) {
            return false;
        }
        int sum = 0, maxNum = 0;
        for (int num : nums) {
            sum += num;
            maxNum = Math.max(maxNum, num);
        }
        if (sum % 2 != 0) {
            return false;
        }
        int target = sum / 2;
        if (maxNum > target) {
            return false;
        }
        boolean[][] dp = new boolean[n][target + 1];
        for (int i = 0; i < n; i++) {
            dp[i][0] = true;
        }
        dp[0][nums[0]] = true;
        for (int i = 1; i < n; i++) {
            int num = nums[i];
            for (int j = 1; j <= target; j++) {
                if (j >= num) {
                    dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[n - 1][target];
    }
}

41 最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

**说明：**每次只能向下或者向右移动一步。

方法：动态规划

class Solution {
    public int minPathSum(int[][] grid) {
        for(int i = 0; i < grid.length; i++) {
            for(int j = 0; j < grid[0].length; j++) {
                if(i == 0 && j == 0) continue;
                else if(i == 0)  grid[i][j] = grid[i][j - 1] + grid[i][j];
                else if(j == 0)  grid[i][j] = grid[i - 1][j] + grid[i][j];
                else grid[i][j] = Math.min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j];
            }
        }
        return grid[grid.length - 1][grid[0].length - 1];
    }
}

42 K 站中转内最便宜的航班

有 n 个城市通过一些航班连接。给你一个数组 flights ，其中 flights[i] = [fromi, toi, pricei] ，表示该航班都从城市 fromi 开始，以价格 pricei 抵达 toi。

现在给定所有的城市和航班，以及出发城市 src 和目的地 dst，你的任务是找到出一条最多经过 k 站中转的路线，使得从 src 到 dst 的 价格最便宜 ，并返回该价格。 如果不存在这样的路线，则输出 -1。

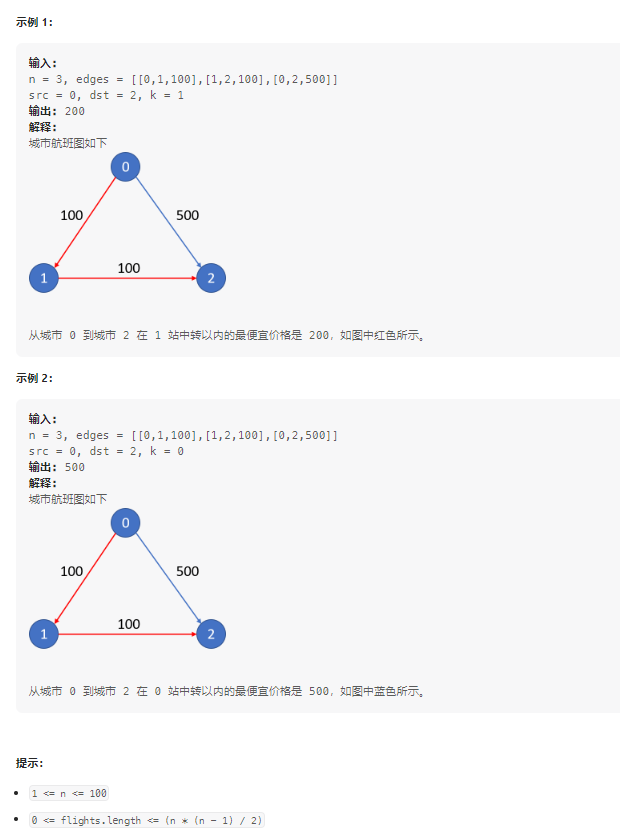
方法：动态规划

class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        final int INF = 10000 * 101 + 1;
        int[][] f = new int[k + 2][n];
        for (int i = 0; i < k + 2; ++i) {
            Arrays.fill(f[i], INF);
        }
        f[0][src] = 0;
        for (int t = 1; t <= k + 1; ++t) {
            for (int[] flight : flights) {
                int j = flight[0], i = flight[1], cost = flight[2];
                f[t][i] = Math.min(f[t][i], f[t - 1][j] + cost);
            }
        }
        int ans = INF;
        for (int t = 1; t <= k + 1; ++t) {
            ans = Math.min(ans, f[t][dst]);
        }
        return ans == INF ? -1 : ans;
    }
}

43 预测赢家

给你一个整数数组 nums 。玩家 1 和玩家 2 基于这个数组设计了一个游戏。

玩家 1 和玩家 2 轮流进行自己的回合，玩家 1 先手。开始时，两个玩家的初始分值都是 0 。每一回合，玩家从数组的任意一端取一个数字（即，nums[0] 或 nums[nums.length - 1]），取到的数字将会从数组中移除（数组长度减 1 ）。玩家选中的数字将会加到他的得分上。当数组中没有剩余数字可取时，游戏结束。

如果玩家 1 能成为赢家，返回 true 。如果两个玩家得分相等，同样认为玩家 1 是游戏的赢家，也返回 true 。你可以假设每个玩家的玩法都会使他的分数最大化。

示例 1：

输入：nums = [1,5,2]
输出：false
解释：一开始，玩家 1 可以从 1 和 2 中进行选择。
如果他选择 2（或者 1 ），那么玩家 2 可以从 1（或者 2 ）和 5 中进行选择。如果玩家 2 选择了 5 ，那么玩家 1 则只剩下 1（或者 2 ）可选。 
所以，玩家 1 的最终分数为 1 + 2 = 3，而玩家 2 为 5 。
因此，玩家 1 永远不会成为赢家，返回 false 。

示例 2：

输入：nums = [1,5,233,7]
输出：true
解释：玩家 1 一开始选择 1 。然后玩家 2 必须从 5 和 7 中进行选择。无论玩家 2 选择了哪个，玩家 1 都可以选择 233 。
最终，玩家 1（234 分）比玩家 2（12 分）获得更多的分数，所以返回 true，表示玩家 1 可以成为赢家。

提示：

• 1 <= nums.length <= 20
• 0 <= nums[i] <= 107

方法：动态规划

class Solution {
    public boolean PredictTheWinner(int[] nums) {
        int length = nums.length;
        int[][] dp = new int[length][length];
        for (int i = 0; i < length; i++) {
            dp[i][i] = nums[i];
        }
        for (int i = length - 2; i >= 0; i--) {
            for (int j = i + 1; j < length; j++) {
                dp[i][j] = Math.max(nums[i] - dp[i + 1][j], nums[j] - dp[i][j - 1]);
            }
        }
        return dp[0][length - 1] >= 0;
    }
}

44 打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。

提示：

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 400

方法：动态规划

如果你对于动态规划还不是很了解，或者没怎么做过动态规划的题目的话，那么 House Robber （小偷问题）这道题是一个非常好的入门题目。本文会以 House Robber 题目为例子，讲解动态规划题目的四个基本步骤。

动态规划的的四个解题步骤是：

定义子问题
写出子问题的递推关系
确定 DP 数组的计算顺序
空间优化（可选）
下面我们一步一步地进行讲解。

步骤一：定义子问题
稍微接触过一点动态规划的朋友都知道动态规划有一个“子问题”的定义。什么是子问题？子问题是和原问题相似，但规模较小的问题。例如这道小偷问题，原问题是“从全部房子中能偷到的最大金额”，将问题的规模缩小，子问题就是“从 kkk 个房子中能偷到的最大金额”，用 f(k)f(k)f(k) 表示。

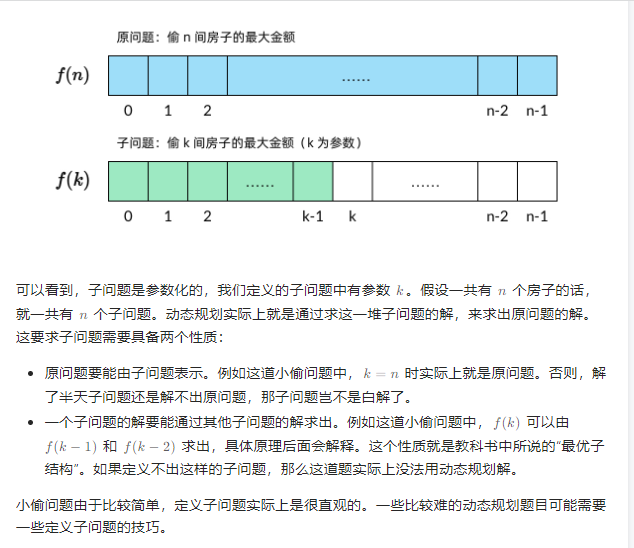
步骤二：写出子问题的递推关系
这一步是求解动态规划问题最关键的一步。然而，这一步也是最无法在代码中体现出来的一步。在做题的时候，最好把这一步的思路用注释的形式写下来。做动态规划题目不要求快，而要确保无误。否则，写代码五分钟，找 bug 半小时，岂不美哉？

我们来分析一下这道小偷问题的递推关系：

步骤三：确定 DP 数组的计算顺序
在确定了子问题的递推关系之后，下一步就是依次计算出这些子问题了。在很多教程中都会写，动态规划有两种计算顺序，一种是自顶向下的、使用备忘录的递归方法，一种是自底向上的、使用 dp 数组的循环方法。不过在普通的动态规划题目中，99% 的情况我们都不需要用到备忘录方法，所以我们最好坚持用自底向上的 dp 数组。

DP 数组也可以叫”子问题数组”，因为 DP 数组中的每一个元素都对应一个子问题。如下图所示，dp[k] 对应子问题 f(k)f(k)f(k)，即偷前 kkk 间房子的最大金额。

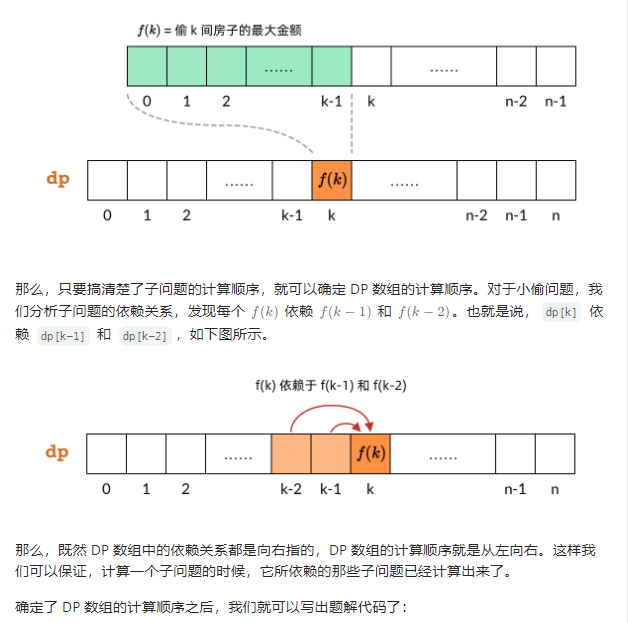
public int rob(int[] nums) {
    if (nums.length == 0) {
        return 0;
    }
    // 子问题：
    // f(k) = 偷 [0..k) 房间中的最大金额

    // f(0) = 0
    // f(1) = nums[0]
    // f(k) = max{ rob(k-1), nums[k-1] + rob(k-2) }

    int N = nums.length;
    int[] dp = new int[N+1];
    dp[0] = 0;
    dp[1] = nums[0];
    for (int k = 2; k <= N; k++) {
        dp[k] = Math.max(dp[k-1], nums[k-1] + dp[k-2]);
    }
    return dp[N];
}

45 买卖股票最佳时间

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

方法：一次遍历

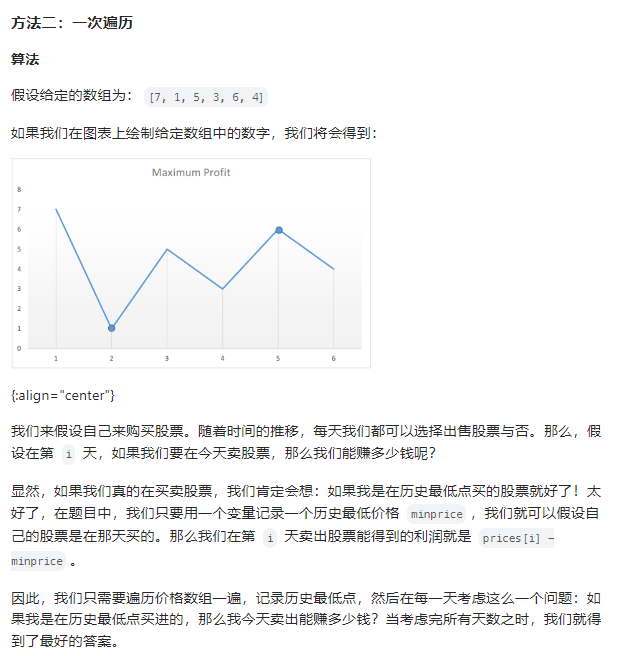
public class Solution {
    public int maxProfit(int prices[]) {
        int minprice = Integer.MAX_VALUE;
        int maxprofit = 0;
        for (int i = 0; i < prices.length; i++) {
            if (prices[i] < minprice) {
                minprice = prices[i];
            } else if (prices[i] - minprice > maxprofit) {
                maxprofit = prices[i] - minprice;
            }
        }
        return maxprofit;
    }
}

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uvVMHzl3-1670180311275)(https://geekmice-blog.oss-cn-beijing.aliyuncs.com/image-20221113141744873.png)]

46 买卖股票的最佳时间II

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
     总利润为 4 + 3 = 7 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     总利润为 4 。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。

提示：

• 1 <= prices.length <= 3 * 104
• 0 <= prices[i] <= 104
• 

public class Solution {

    public int maxProfit(int[] prices) {
        int len = prices.length;
        if (len < 2) {
            return 0;
        }

        // 0：持有现金
        // 1：持有股票
        // 状态转移：0 → 1 → 0 → 1 → 0 → 1 → 0
        int[][] dp = new int[len][2];

        dp[0][0] = 0;
        dp[0][1] = -prices[0];

        for (int i = 1; i < len; i++) {
            // 这两行调换顺序也是可以的
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        }
        return dp[len - 1][0];
    }
}

50 买卖股票的最佳时机含手续费

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

**注意：**这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

示例 1：

输入：prices = [1, 3, 2, 8, 4, 9], fee = 2
输出：8
解释：能够达到的最大利润:  
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8

示例 2：

输入：prices = [1,3,7,5,10,3], fee = 3
输出：6

提示：

• 1 <= prices.length <= 5 * 10^4
• 1 <= prices[i] < 5 * 10^4
• 0 <= fee < 5 * 10^4

class Solution {
    public int maxProfit(int[] prices, int fee) {
        int n = prices.length;
        int[][] dp = new int[n][2];
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for (int i = 1; i < n; ++i) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        }
        return dp[n - 1][0];
    }
}

47 最长回文子序列

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例 1：

输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。

示例 2：

输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。

提示：

• 1 <= s.length <= 1000
• s 仅由小写英文字母组成

class Solution {
    public int longestPalindromeSubseq(String s) {
        int n = s.length();
        int[][] dp = new int[n][n];
        for (int i = n - 1; i >= 0; i--) {
            dp[i][i] = 1;
            char c1 = s.charAt(i);
            for (int j = i + 1; j < n; j++) {
                char c2 = s.charAt(j);
                if (c1 == c2) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[0][n - 1];
    }
}

二叉树

48 二叉树最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3 。

方法一：深度优先搜索

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            int leftHeight = maxDepth(root.left);
            int rightHeight = maxDepth(root.right);
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }
}

方法二：广度优先搜索

思路与算法

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        int ans = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size > 0) {
                TreeNode node = queue.poll();
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if (node.right != null) {
                    queue.offer(node.right);
                }
                size--;
            }
            ans++;
        }
        return ans;
    }
}

49 二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1：

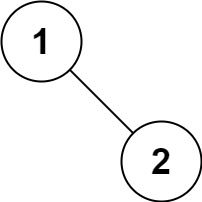
输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

输入：root = [1,2]
输出：[1,2]

示例 5：

输入：root = [1,null,2]
输出：[1,2]

提示：

• 树中节点数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

前序遍历

public static void preOrderRecur(TreeNode head) {
    if (head == null) {
        return;
    }
    System.out.print(head.value + " ");
    preOrderRecur(head.left);
    preOrderRecur(head.right);
}

中序遍历

public static void preOrderRecur(TreeNode head) {
    if (head == null) {
        return;
    }
    preOrderRecur(head.left);
    System.out.print(head.value + " ");
    preOrderRecur(head.right);
}

后序遍历

public static void postOrderRecur(TreeNode head) {
    if (head == null) {
        return;
    }
    postOrderRecur(head.left);
    postOrderRecur(head.right);
    System.out.print(head.value + " ");
}

50 二叉树的直径

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

示例 :
给定二叉树

          1
         / \
        2   3
       / \     
      4   5    

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

**注意：**两结点之间的路径长度是以它们之间边的数目表示。

方法一：深度优先搜索
首先我们知道一条路径的长度为该路径经过的节点数减一，所以求直径（即求路径长度的最大值）等效于求路径经过节点数的最大值减一。

而任意一条路径均可以被看作由某个节点为起点，从其左儿子和右儿子向下遍历的路径拼接得到。

class Solution {
    int ans;
    public int diameterOfBinaryTree(TreeNode root) {
        ans = 1;
        depth(root);
        return ans - 1;
    }
    public int depth(TreeNode node) {
        if (node == null) {
            return 0; // 访问到空节点了，返回0
        }
        int L = depth(node.left); // 左儿子为根的子树的深度
        int R = depth(node.right); // 右儿子为根的子树的深度
        ans = Math.max(ans, L+R+1); // 计算d_node即L+R+1 并更新ans
        return Math.max(L, R) + 1; // 返回该节点为根的子树的深度
    }
}

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zIx1W7BG-1670180311291)(C:/Users/PMB/AppData/Roaming/Typora/typora-user-images/image-20221113143422181.png)]

51 二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

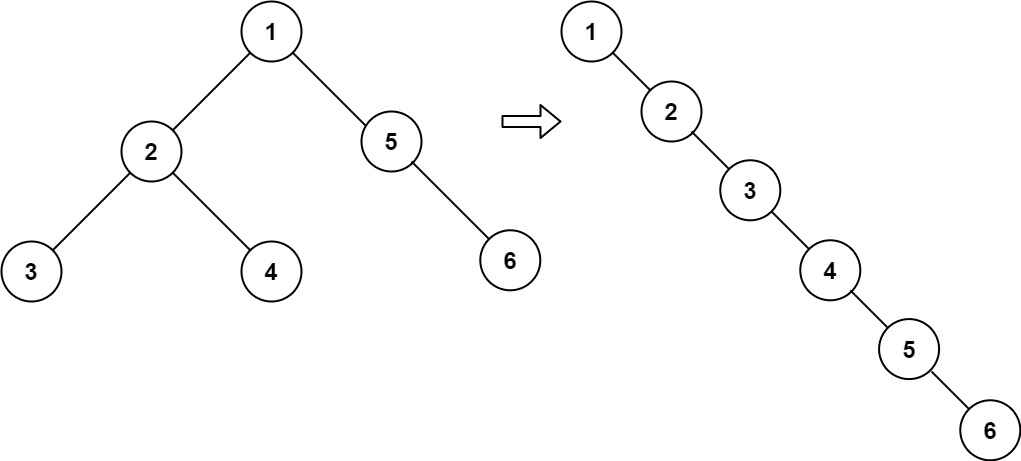
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [0]
输出：[0]

提示：

• 树中结点数在范围 [0, 2000] 内
• -100 <= Node.val <= 100

前序遍历

方法一：前序遍历
将二叉树展开为单链表之后，单链表中的节点顺序即为二叉树的前序遍历访问各节点的顺序。因此，可以对二叉树进行前序遍历，获得各节点被访问到的顺序。由于将二叉树展开为链表之后会破坏二叉树的结构，因此在前序遍历结束之后更新每个节点的左右子节点的信息，将二叉树展开为单链表。

对二叉树的前序遍历不熟悉的读者请自行练习「144. 二叉树的前序遍历」。

前序遍历可以通过递归或者迭代的方式实现。以下代码通过递归实现前序遍历

class Solution {
    public void flatten(TreeNode root) {
        List<TreeNode> list = new ArrayList<TreeNode>();
        preorderTraversal(root, list);
        int size = list.size();
        for (int i = 1; i < size; i++) {
            TreeNode prev = list.get(i - 1), curr = list.get(i);
            prev.left = null;
            prev.right = curr;
        }
    }

    public void preorderTraversal(TreeNode root, List<TreeNode> list) {
        if (root != null) {
            list.add(root);
            preorderTraversal(root.left, list);
            preorderTraversal(root.right, list);
        }
    }
}

52 填充每个节点的下一个右侧节点指针

\116. 填充每个节点的下一个右侧节点指针

中等

899

相关企业

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

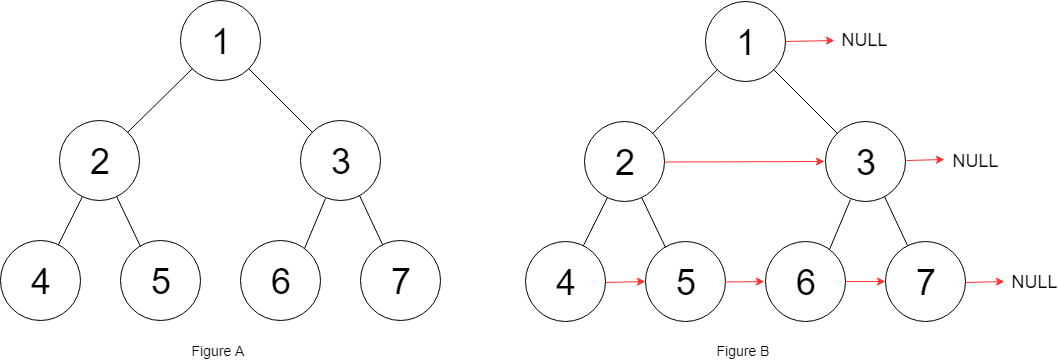
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

示例 2:

输入：root = []
输出：[]

提示：

• 树中节点的数量在 [0, 212 - 1] 范围内
• -1000 <= node.val <= 1000

进阶：

• 你只能使用常量级额外空间。
• 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

层次遍历

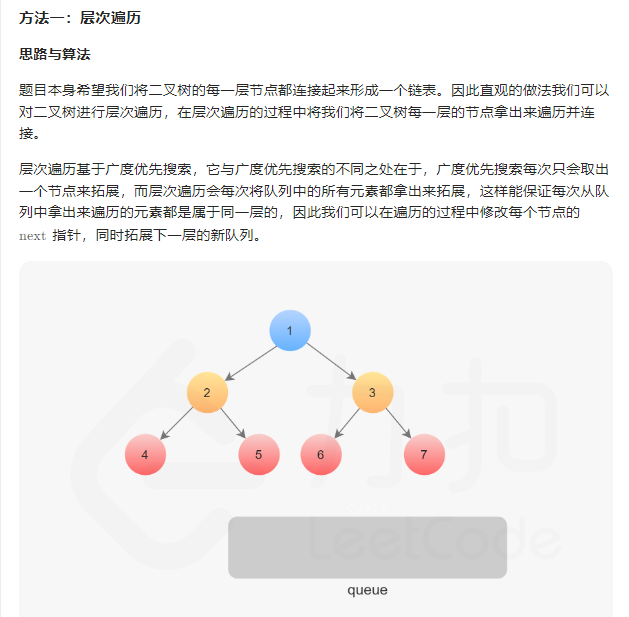
class Solution {
    public Node connect(Node root) {
        if (root == null) {
            return root;
        }
        
        // 初始化队列同时将第一层节点加入队列中，即根节点
        Queue<Node> queue = new LinkedList<Node>(); 
        queue.add(root);
        
        // 外层的 while 循环迭代的是层数
        while (!queue.isEmpty()) {
            
            // 记录当前队列大小
            int size = queue.size();
            
            // 遍历这一层的所有节点
            for (int i = 0; i < size; i++) {
                
                // 从队首取出元素
                Node node = queue.poll();
                
                // 连接
                if (i < size - 1) {
                    node.next = queue.peek();
                }
                
                // 拓展下一层节点
                if (node.left != null) {
                    queue.add(node.left);
                }
                if (node.right != null) {
                    queue.add(node.right);
                }
            }
        }
        
        // 返回根节点
        return root;
    }
}

53 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

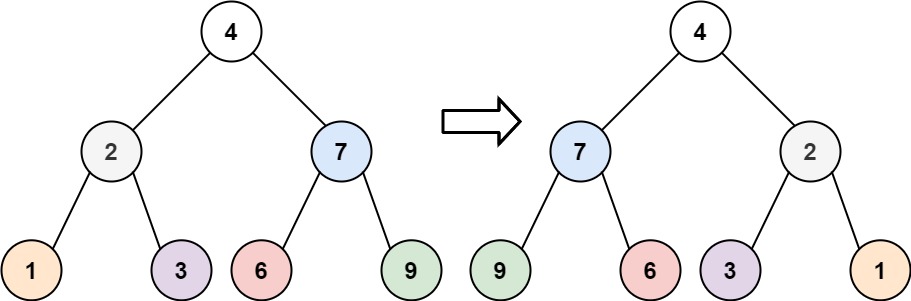
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

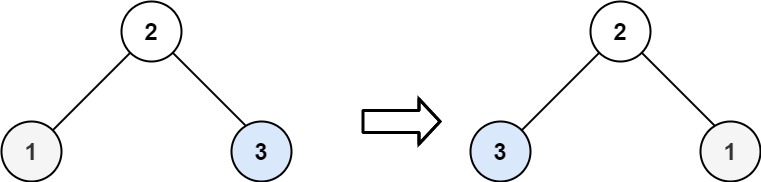
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目范围在 [0, 100] 内
• -100 <= Node.val <= 100

递归

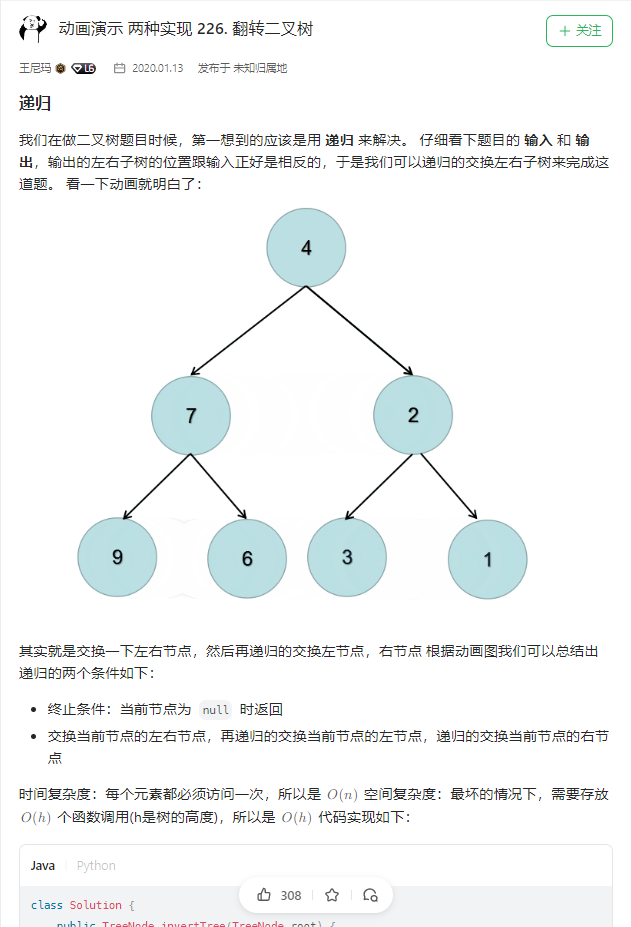
class Solution {
	public TreeNode invertTree(TreeNode root) {
		//递归函数的终止条件，节点为空时返回
		if(root==null) {
			return null;
		}
		//下面三句是将当前节点的左右子树交换
		TreeNode tmp = root.right;
		root.right = root.left;
		root.left = tmp;
		//递归交换当前节点的 左子树
		invertTree(root.left);
		//递归交换当前节点的 右子树
		invertTree(root.right);
		//函数返回时就表示当前这个节点，以及它的左右子树
		//都已经交换完了
		return root;
	}
}

54 二叉树的镜像

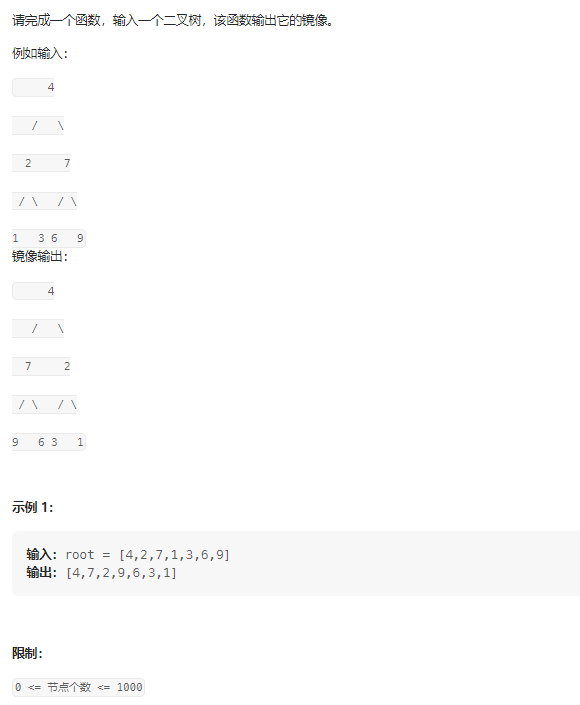
递归

class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        TreeNode left = mirrorTree(root.left);
        TreeNode right = mirrorTree(root.right);
        root.left = right;
        root.right = left;
        return root;
    }
}

55 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

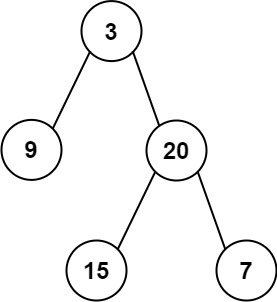
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

递归

class Solution {
    private Map<Integer, Integer> indexMap;

    public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        if (preorder_left > preorder_right) {
            return null;
        }

        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;
        // 在中序遍历中定位根节点
        int inorder_root = indexMap.get(preorder[preorder_root]);
        
        // 先把根节点建立出来
        TreeNode root = new TreeNode(preorder[preorder_root]);
        // 得到左子树中的节点数目
        int size_left_subtree = inorder_root - inorder_left;
        // 递归地构造左子树，并连接到根节点
        // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
        root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
        // 递归地构造右子树，并连接到根节点
        // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        // 构造哈希映射，帮助我们快速定位根节点
        indexMap = new HashMap<Integer, Integer>();
        for (int i = 0; i < n; i++) {
            indexMap.put(inorder[i], i);
        }
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }
}

56 从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

class Solution {
    int post_idx;
    int[] postorder;
    int[] inorder;
    Map<Integer, Integer> idx_map = new HashMap<Integer, Integer>();

    public TreeNode helper(int in_left, int in_right) {
        // 如果这里没有节点构造二叉树了，就结束
        if (in_left > in_right) {
            return null;
        }

        // 选择 post_idx 位置的元素作为当前子树根节点
        int root_val = postorder[post_idx];
        TreeNode root = new TreeNode(root_val);

        // 根据 root 所在位置分成左右两棵子树
        int index = idx_map.get(root_val);

        // 下标减一
        post_idx--;
        // 构造右子树
        root.right = helper(index + 1, in_right);
        // 构造左子树
        root.left = helper(in_left, index - 1);
        return root;
    }

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        this.postorder = postorder;
        this.inorder = inorder;
        // 从后序遍历的最后一个元素开始
        post_idx = postorder.length - 1;

        // 建立（元素，下标）键值对的哈希表
        int idx = 0;
        for (Integer val : inorder) {
            idx_map.put(val, idx++);
        }
        
        return helper(0, inorder.length - 1);
    }
}

57 最大二叉树

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

1. 创建一个根节点，其值为 nums 中的最大值。
2. 递归地在最大值 左边 的 子数组前缀上 构建左子树。
3. 递归地在最大值 右边 的 子数组后缀上 构建右子树。

返回 nums 构建的 *最大二叉树* 。

示例 1：

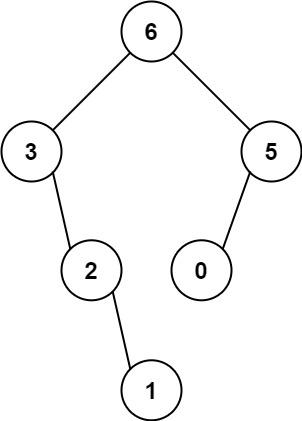
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000
• nums 中的所有整数 互不相同

递归

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return construct(nums, 0, nums.length - 1);
    }

    public TreeNode construct(int[] nums, int left, int right) {
        if (left > right) {
            return null;
        }
        int best = left;
        for (int i = left + 1; i <= right; ++i) {
            if (nums[i] > nums[best]) {
                best = i;
            }
        }
        TreeNode node = new TreeNode(nums[best]);
        node.left = construct(nums, left, best - 1);
        node.right = construct(nums, best + 1, right);
        return node;
    }
}

单调栈

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        int n = nums.length;
        Deque<Integer> stack = new ArrayDeque<Integer>();
        int[] left = new int[n];
        int[] right = new int[n];
        Arrays.fill(left, -1);
        Arrays.fill(right, -1);
        TreeNode[] tree = new TreeNode[n];
        for (int i = 0; i < n; ++i) {
            tree[i] = new TreeNode(nums[i]);
            while (!stack.isEmpty() && nums[i] > nums[stack.peek()]) {
                right[stack.pop()] = i;
            }
            if (!stack.isEmpty()) {
                left[i] = stack.peek();
            }
            stack.push(i);
        }

        TreeNode root = null;
        for (int i = 0; i < n; ++i) {
            if (left[i] == -1 && right[i] == -1) {
                root = tree[i];
            } else if (right[i] == -1 || (left[i] != -1 && nums[left[i]] < nums[right[i]])) {
                tree[left[i]].right = tree[i];
            } else {
                tree[right[i]].left = tree[i];
            }
        }
        return root;
    }
}

58 根据前序和后序遍历构造二叉树

给定两个整数数组，preorder 和 postorder ，其中 preorder 是一个具有 无重复 值的二叉树的前序遍历，postorder 是同一棵树的后序遍历，重构并返回二叉树。

如果存在多个答案，您可以返回其中 任何 一个。

示例 1：

输入：preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1]
输出：[1,2,3,4,5,6,7]

示例 2:

输入: preorder = [1], postorder = [1]
输出: [1]

提示：

• 1 <= preorder.length <= 30
• 1 <= preorder[i] <= preorder.length
• preorder 中所有值都 不同
• postorder.length == preorder.length
• 1 <= postorder[i] <= postorder.length
• postorder 中所有值都 不同
• 保证 preorder 和 postorder 是同一棵二叉树的前序遍历和后序遍历

class Solution {
    int[] pre, post;
    public TreeNode constructFromPrePost(int[] pre, int[] post) {
        this.pre = pre;
        this.post = post;
        return make(0, 0, pre.length);
    }

    public TreeNode make(int i0, int i1, int N) {
        if (N == 0) return null;
        TreeNode root = new TreeNode(pre[i0]);
        if (N == 1) return root;

        int L = 1;
        for (; L < N; ++L)
            if (post[i1 + L-1] == pre[i0 + 1])
                break;

        root.left = make(i0+1, i1, L);
        root.right = make(i0+L+1, i1+L, N-1-L);
        return root;
    }
}

59 重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

限制：

0 <= 节点个数 <= 5000

递归

class Solution {
    private Map<Integer, Integer> indexMap;

    public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        if (preorder_left > preorder_right) {
            return null;
        }

        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;
        // 在中序遍历中定位根节点
        int inorder_root = indexMap.get(preorder[preorder_root]);
        
        // 先把根节点建立出来
        TreeNode root = new TreeNode(preorder[preorder_root]);
        // 得到左子树中的节点数目
        int size_left_subtree = inorder_root - inorder_left;
        // 递归地构造左子树，并连接到根节点
        // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
        root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
        // 递归地构造右子树，并连接到根节点
        // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        // 构造哈希映射，帮助我们快速定位根节点
        indexMap = new HashMap<Integer, Integer>();
        for (int i = 0; i < n; i++) {
            indexMap.put(inorder[i], i);
        }
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }
}

60 寻找重复的子树

给你一棵二叉树的根节点 root ，返回所有 重复的子树 。

对于同一类的重复子树，你只需要返回其中任意 一棵 的根结点即可。

如果两棵树具有 相同的结构 和 相同的结点值 ，则认为二者是 重复 的。

示例 1：

输入：root = [1,2,3,4,null,2,4,null,null,4]
输出：[[2,4],[4]]

示例 2：

输入：root = [2,1,1]
输出：[[1]]

示例 3：

输入：root = [2,2,2,3,null,3,null]
输出：[[2,3],[3]]

提示：

• 树中的结点数在 [1, 5000] 范围内。
• -200 <= Node.val <= 200

三元组

class Solution {
    Map<String, Pair<TreeNode, Integer>> seen = new HashMap<String, Pair<TreeNode, Integer>>();
    Set<TreeNode> repeat = new HashSet<TreeNode>();
    int idx = 0;

    public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
        dfs(root);
        return new ArrayList<TreeNode>(repeat);
    }

    public int dfs(TreeNode node) {
        if (node == null) {
            return 0;
        }
        int[] tri = {node.val, dfs(node.left), dfs(node.right)};
        String hash = Arrays.toString(tri);
        if (seen.containsKey(hash)) {
            Pair<TreeNode, Integer> pair = seen.get(hash);
            repeat.add(pair.getKey());
            return pair.getValue();
        } else {
            seen.put(hash, new Pair<TreeNode, Integer>(node, ++idx));
            return idx;
        }
    }
}