快速排序的详解
主要讲解快速排序的递归的三种实现方法和非递归的实现方法.
目录
递归版本
1.Hoare经典版
2.挖坑法
3.前后指针法
非递归版本:
递归版本
1.Hoare经典版
单趟排序思想:
1.选取最左边值为key,然后从右边开始向左找小于key的值.
2.找到之后,左边再走,找到大于key的值.
3.左边也找到之后,交换两个值.
4.右边继续向做找,找到之后,左边再继续向后找,找到之后再次进行交换,如此反复.
5.直到两者相遇,选最左边的值与key交换.
此时key就在正确的位置上.
看以下动图来理解单趟排序.

图片来源于网络.
所以每次找到keyi值以后,再次找keyi剩下两侧的keyi值,然后再次划分,如此反复...
下面是代码实现:
int partion1(int* a, int left, int right)
{
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])//从右开始向左找,直到找到小于a[keyi]的值
{
right--;
}
while (left < right && a[left] <= a[keyi])//从左边开始向右找,直到找打大于a[keyi]的值
{
left++;
}
swap(a[left], a[right]);//交换两个值
}
swap(a[keyi], a[left]);//swap(a[keyi],a[right])也可以,因为此时left和right相遇了,left=right
return left;//此时keyi值已经到了left(right)的位置,返回即可
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
{
return;
}
int keyi = partion1(a, left, right);
//[left,keyi-1], keyi,[keyi+1.right]
//开始排序[left,keyi-1]
QuickSort(a, left, keyi - 1);
//开始排序[keyi+1,right]
QuickSort(a, keyi + 1, right);
}2.挖坑法
这一步是hoare法的一种变形.
单趟排序思想:
1.先将最左边的数据存放在临时变量key中,然后就当此处形成一个坑位.
2.然后从右开始想左找,若小于key,则把这个值放到那个坑位中,然后本身的位置形成一个新的坑位.
3.再从左向右找,若大于key,则放到上一步形成的坑位中,本身的位置也形成一个坑位.
4.循环步骤123
5.两者相遇时,一定会有一个坑位,将key值放到其中即可.
动图如下:

图片来源于网络.
每次返回坑位的的值下标(left,right均可),并且不断缩小范围,再划分,找key,直至全部排序完毕.
int partion2(int* a, int left, int right)
{
int key = a[left];
int piti = left;
while (left < right)
{
while (left < right && a[right] > key)//从右向左找,直到找到小于key的值
{
right--;
}
//将a[right]的值放入到坑位中
a[piti] = a[right];
//并在这个位置重新形成坑位
piti = right;
while (left < right && a[left] < key)//从左向右找,直到找打大于key的值
{
left++;
}
a[piti] = a[left];
piti = left;
}
//相遇之后,把key值放到坑位中,此时key已经到了正确位置
a[piti] = key;
//返回此时坑位下标
return piti;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
{
return;
}
int keyi = partion2(a, left, right);
//[left,keyi-1], keyi,[keyi+1.right]
//开始排序[left,keyi-1]
QuickSort(a, left, keyi - 1);
//开始排序[keyi+1,right]
QuickSort(a, keyi + 1, right);
}3.前后指针法
这是我们推荐的一种写法.
基本思想:
1.选取prev为序列的开始,cur为prev的下一个位置,同时选取最左边的下标值为keyi.
2.cur先走,找到小于key的值,停下来.
3.prev++
4.此时再交换a[prev]和a[cur]的值
5.一种重复2,3,4步,直到停止,交换key和prev的值
此时key值就在正确位置了.
在这个过程中,prev相当于是维护小于key的值,这样停下来时,prev前面的全是小于key的值,所以此时交换key和prev,prev就是正确位置了.
动图如下:
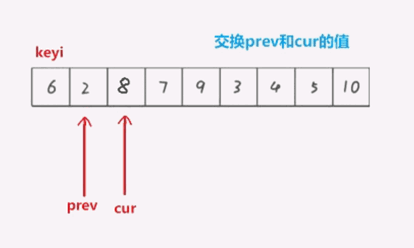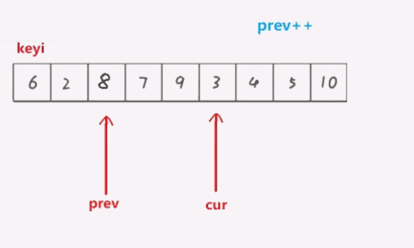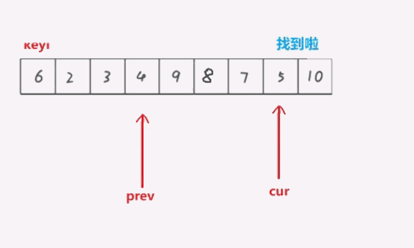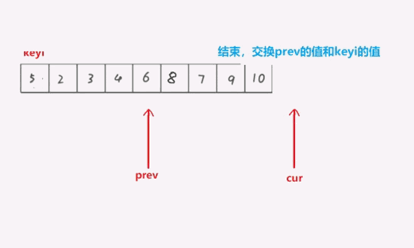
int partion3(int* a, int left, int right)
{
int prev = left;
int cur = left + 1;
int keyi = left;
while (cur <= right)
{
if (a[cur] < a[keyi])//如果a[cur]的值小于a[keyi]
{
prev++;//先prev++;
swap(a[cur], a[prev]);//再交换prev和cur的值.
}
cur++;
}
swap(a[keyi], a[prev]);//最后交换a[keyi]和a[prev]的值
keyi = prev;
return keyi;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
{
return;
}
int keyi = partion3(a, left, right);
//[left,keyi-1], keyi,[keyi+1.right]
//开始排序[left,keyi-1]
QuickSort(a, left, keyi - 1);
//开始排序[keyi+1,right]
QuickSort(a, keyi + 1, right);
}
非递归版本:
递归有个大问题就是当数据量过大时,在极端情况下,会对栈的开销太大,造成栈溢出.
所以这个时候有两种:
一种是改成循环
第二是用栈来模拟递归,因为栈本质是用数组,这个范围可是非常大的.所以这个题就用栈来模拟递归.
递归版本的主要过程就是在不断的划分子区间,所以如果非递归实现快排,就用栈来保存它的区间并不断划分保存
基本思想:
1.申请一个栈,用来保存数组的起始和终点位置.
2.将整个数组的起始位置和重点位置入栈(由于栈的特性是先进后出,后进先出,所以先入right,再入left)
3.定义begin来接受栈顶元素、进栈操作,end接受栈顶操作,出栈操作
4.对数组进行一次单趟排序,保存keyi值,即关键值下标.
5. 这时候需要排基准值key左边的序列。
把右区间的左右范围值压入栈中
压完之后,再把左区间的左右范围压入.
(反了也可以,只不过成了先遍历划分右区间,再划分左区间了)
6.判断栈是否为空,不为空,重复4,5步,若为空,说明所有元素已经排序完毕.
代码如下:
void QuickSortNonR(int* a, int begin, int end)
{
stack<int> st;
st.push(end);//先取整个数组的终点位置
st.push(begin);//再去起始位置.
while (!st.empty())
{
int left = st.top();//由于栈后进先出,所以取出的是begin
st.pop();
int right = st.top();//取出end
st.pop();
int keyi = partion3(a,left,right);//保存排序好的keyi值
//递归模拟过程
if (keyi + 1 < right)//如果右区间还存在,则继续划分,并把右区间左右范围存放到栈中
{
st.push(right);
st.push(keyi + 1);
}
if (left < keyi - 1)/如果左区间还存在,则继续划分,并把左区间左右范围存放到栈中
{
st.push(keyi - 1);
st.push(left);
}
}
}这就是快速排序的全部内容啦,如果有疑问或错误的地方,欢迎提问或指正哦!
