13. K近邻模型

设某回归任务的输入包含两个变量，将它们的值视为平面上点的坐标。如图2.1所示，灰点代表训练数据中的输入，白点代表输出待预测的输入。假如采用2.3节介绍的平均值法，当白点与黑点重合时，因为在该处只有一个训练实例，所以平均值不能很好地代表期望值；而当白点处于更有可能的其他位置时，因为在该处没有训练实例，无法预测输出值。为走出此困境，自然的想法是，在计算平均值时，扩大取其输出的实例的范围。假设输出待预测的输入为x，原来要求找到训练数据中输入等于x的实例，现在则放宽到所有输入处于x的某邻域的实例。在图2.1中，以白点为中心所画的圆就代表一个这样的区域，在该区域内，可用于为白点取平均值的灰点有8个。

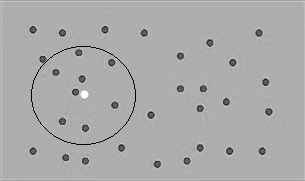
图2.1 某个输入邻近区域内的实例

用数学语言表达，就是用以下函数 作为 的近似：

其中N(x)表示x的某个邻域。使用给定区域的条件期望来代替给定点的条件期望，解决了预测时输入处训练数据太少或不存在的难题。在实际应用中，期望用平均值计算，邻域的选择标准则是其中包含预定数量（以K表示）的训练数据实例，于是有：

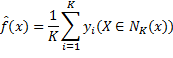
NK(x)表示x的包含最近K个实例的邻域。这就是K近邻（K nearest neighbors）回归模型的思想。为了认识该模型的归纳偏好，考虑最简单的单个输入变量的情况。如图2.2所示，X轴代表输入，Y轴代表输出，训练数据实例的输入用灰叉标记在X轴上，对应的输出用圆点标记在它们上方，K取值3。假设某个待预测的输入位于黑叉标记处，它近邻的3个训练实例为，最靠近它的左侧两个和右侧一个灰叉。输出的预测值为这三个实例输出的平均值，在图中用三角形标记。假如查询的输入值略微减少，预测值会有何变化？由图中可看出，输入值的近邻仍然是原来那三个数据实例。查询的输入值略微增加的情况也一样。实际上，只要查询的输入值保持在图中用黑色线段标记的区域内，它的近邻都不会改变，这些近邻的输出的平均值也不会改变。这就是K近邻模型所用的归纳偏好——在输入空间的邻域内，预测函数值保持不变。一般而言，函数的输入值接近，输出值也接近。例如，当两个输入值之差趋近0时，连续函数的输出值只差也趋近0。当然，并非所有函数在所有输入处皆如此，K近邻模型如此假设，是为了在合理的基础上求出预测函数。

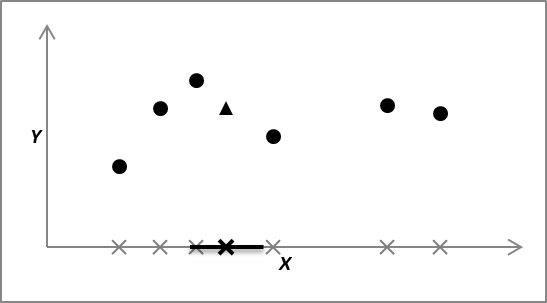
图2.2 K近邻模型的预测函数值在输入空间的邻域内是不变的

值得辨析的是，预测函数值保持不变的区域，并非查询数据点周围的包含K个最近邻实例的区域——它仅是在其中取用于预测输出值的实例的区域——而是与查询数据点拥有相同的K个最近邻实例的数据点组成的区域。否则，假如在某个数据点周围的包含K个最近邻的区域内预测函数值保持不变，那么对于处于该区域边缘处的另一数据点，也可以画出其周围的包含K个最近邻的区域，预测函数值在该区域内保持不变，如此不断扩展，就会得出在整个输入空间上预测函数值都保持不变的荒唐结论。

由概率论可知，K取值越大，平均值越稳定；训练实例的总数N越大，K和N的比值K/N越小，给定一个区域的条件期望就越接近给定一个点的条件期望；当K和N趋近无穷大，且K/N趋近0时，K近邻模型的预测值就逼近2.2.1节给出的理论回归函数值。

这似乎表明K近邻是理想的模型，不过实际上N不可能无穷大，获取巨大的训练数据集并非易事。此外，当输入变量众多时，例如在1000维的输入向量空间中，训练数据点很可能相距遥远，拥有相同K个最近邻的区域变得很大，假定预测函数值在如此大的区域内保持不变，并不合理，因此不宜应用K近邻模型。

下面再来看如何用K近邻模型分类。根据0–1损失最小化标准，输出的预测值是给定输入下条件概率最大的类别。与回归类似，用给定区域的条件概率来代替给定点的条件概率。具体而言，当我们要预测输入空间中某点处的类别时，就找出与它距离最近的K个点，然后检查它们的类别。计算每个类别出现的次数，再除以K，就得到查询点的邻域内各类别的条件概率，其中最大值对应的类别就是查询点的预测类别。由于这些概率分数的分母都是K，所以只需比较分子的大小，也就是说，查询点的预测类别为其K个最近邻中出现次数最多的类别，这就是K近邻分类模型的思想。K近邻回归模型的注意事项对于分类模型同样适用：只有当训练实例数和近邻数K都足够大时，预测才准确和稳定，因此不宜用于高维输入空间。