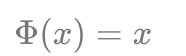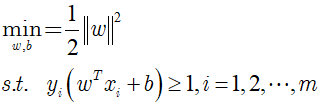机器学习SVM算法原理
目录
- 1 定义输入数据
- 2 线性可分支持向量机
- 3 SVM的计算过程与算法步骤
- 3.1 推导目标函数
- 3.2 目标函数的求解
- 3.2.1 朗格朗日乘子法
- 3.2.2 对偶问题
- 3.2.3 整体流程确定
- 4 举例
- 5 小结
1 定义输入数据
假设给定一个特征空间上的训练集为:
T={(x_1, y_1),(x_2,y_2)…,(x_N,y_N)}T={(x1,y1),(x2,y2)…,(x**N,y**N)}
x_i \in R^n, y_i \in {+1, -1}, i=1,2,…,N.x**i∈R**n,y**i∈{+1,−1},i=1,2,…,N.
其中,(xi,yi)称为样本点。
- xi为第i个实例(样本),
- yi为的xi标记:
- 当yi=1时,为xi正例
- 当yi=-1时,为xi负例
至于为什么正负用(-1,1)表示呢?
其实这里没有太多原理,就是一个标记,你也可以用(2,-3)来标记。只是为了方便,y_i/y_j=y_iy_jyi*/*yj*=y**i∗y**j的过程中刚好可以相等,便于之后的计算。)
2 线性可分支持向量机
给定了上面提出的线性可分训练数据集,通过间隔最大化得到分离超平面为 :y(x)=w^T\Phi(x)+by(x)=w**TΦ(x)+b
相应的分类决策函数为: f(x)=sign(w^T\Phi(x)+b)f(x)=sig**n(w**TΦ(x)+b)
以上决策函数就称为线性可分支持向量机。
这里解释一下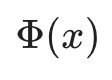 这个东东。
这个东东。
这是某个确定的特征空间转换函数,它的作用是将x映射到更高的维度,它有一个以后我们经常会见到的专有称号**”核函数“**。
比如我们看到的特征有2个: x1,x2,组成最先见到的线性函数可以是:
但也许这两个特征并不能很好地描述数据,于是我们进行维度的转化,变成了:w_1x_1+w_2x_2+w_3x_1x_2+w_4x_12+w_5x_22w1x1+w2x2+w3x1x2+w4x12+w5x22. 于是我们多了三个特征。而这个就是笼统地描述x的映射的。 最简单直接的就是:
以上就是线性可分支持向量机的模型表达式。我们要去求出这样一个模型,或者说这样一个超平面y(x),它能够最优地分离两个集合。
其实也就是我们要去求一组参数(w,b),使其构建的超平面函数能够最优地分离两个集合。
如下就是一个最优超平面:
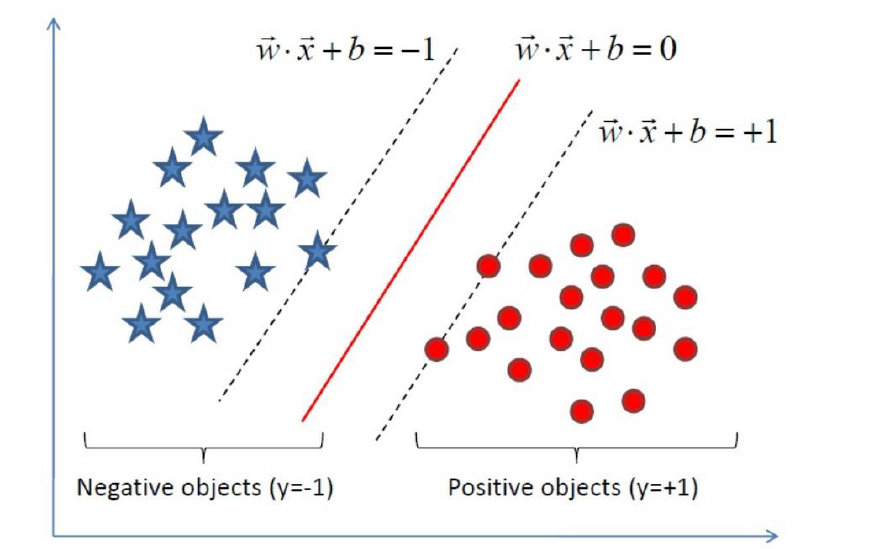
又比如说这样:
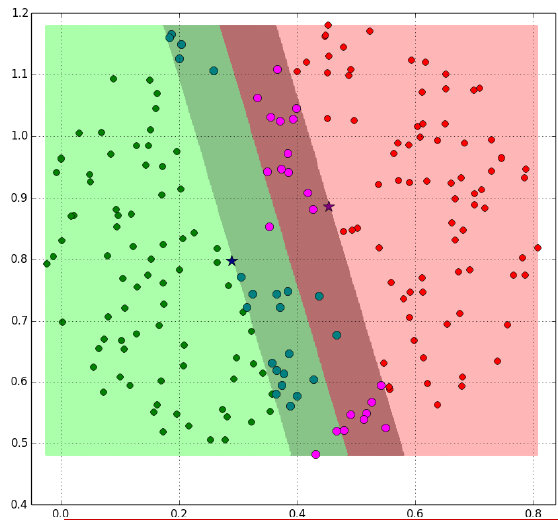
阴影部分是一个“过渡带”,“过渡带”的边界是集合中离超平面最近的样本点落在的地方。
3 SVM的计算过程与算法步骤
3.1 推导目标函数
我们知道了支持向量机是个什么东西了。现在我们要去寻找这个支持向量机,也就是寻找一个最优的超平面。
于是我们要建立一个目标函数。那么如何建立呢?
再来看一下我们的超平面表达式: y(x)=w^T\Phi(x)+by(x)=w**TΦ(x)+b
为了方便我们让:\Phi(x)=xΦ(x)=x
则在样本空间中,划分超平面可通过如下线性方程来描述:w^Tx+b=0wTx+b=0
- 我们知道
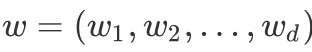 为法向量,决定了超平面的方向;
为法向量,决定了超平面的方向; - b为位移项,决定了超平面和原点之间的距离。
- 显然,划分超平面可被法向量w和位移b确定,我们把其记为(w,b).
样本空间中任意点x到超平面(w,b)的距离可写成
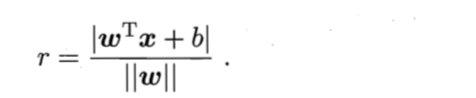
假设超平面(w, b)能将训练样本正确分类,即对于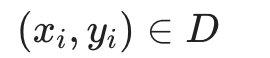 ,
,
- 若yi=+1,则有
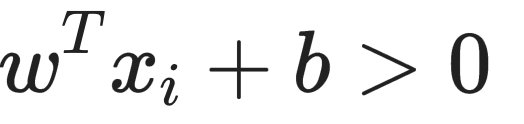 ;
; - 若yi=-1,则有
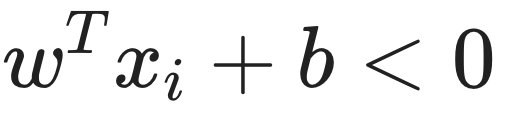 ;
;
令
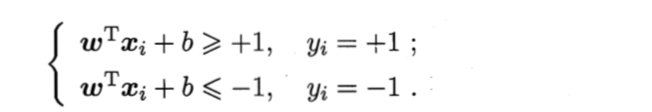
如图所示,距离超平面最近的几个训练样本点使上式等号成立,他们被称为“支持向量",
两个异类支持向量到超平面的距离之和为: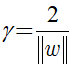 ;
;
它被称为“”间隔“”。
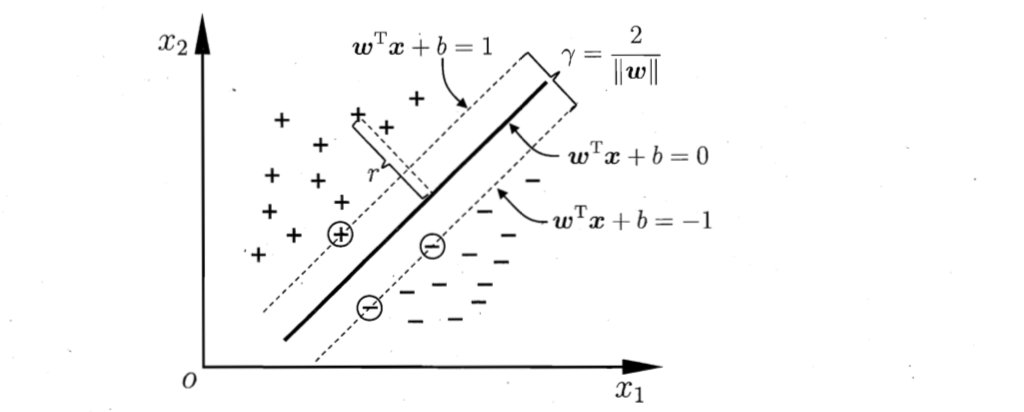
欲找到具有最大间隔的划分超平面,也就是要找到能满足下式中约束的参数w和b,使得 r 最大。
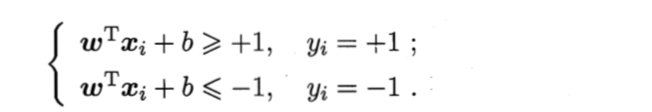
即:
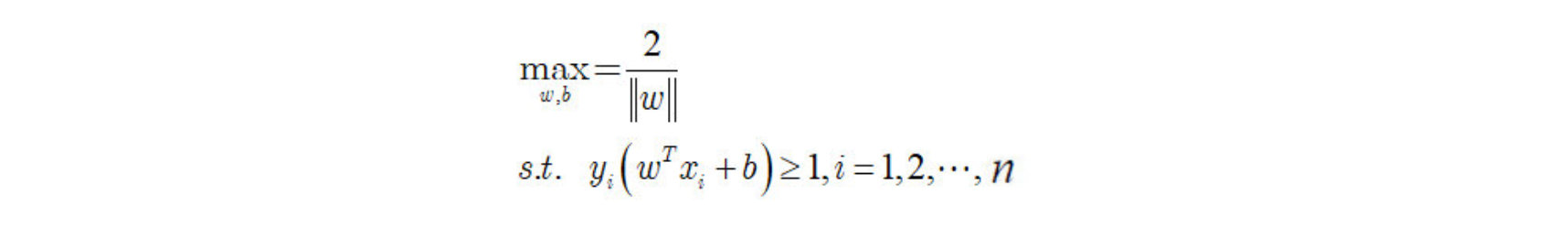
显然,为了最大化间隔,仅需要最大化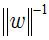 ,这等价于最小化
,这等价于最小化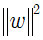 。于是上式可以重写为:
。于是上式可以重写为:
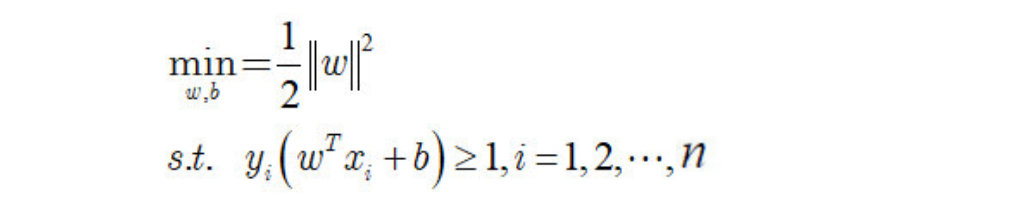
这就是支持向量机的基本型。
拓展:什么是 ||w||?
3.2 目标函数的求解
到这一步,终于把目标函数给建立起来了。
那么下一步自然是去求目标函数的最优值.
因为目标函数带有一个约束条件,所以我们可以用拉格朗日乘子法求解。
3.2.1 朗格朗日乘子法
啥是拉格朗日乘子法呢?
拉格朗日乘子法 (Lagrange multipliers)是一种寻找多元函数在一组约束下的极值的方法.
通过引入拉格朗日乘子,可将有 d 个变量与 k 个约束条件的最优化问题转化为具有 d + k 个变量的无约束优化问题求解。
经过朗格朗日乘子法,我们可以把目标函数转换为:
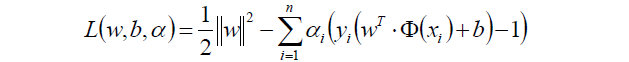
然后我们令:
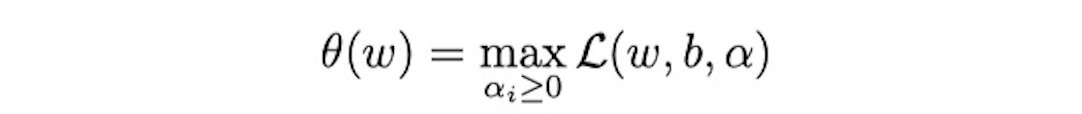
容易验证,当某个约束条件不满足时,例如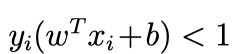 ,那么显然有 θ(w) = ∞ (只要令 αi = ∞ 即可)。而当所有约束条件都满足时,则有
,那么显然有 θ(w) = ∞ (只要令 αi = ∞ 即可)。而当所有约束条件都满足时,则有 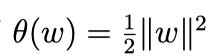 ,亦即最初要 最小化的量。
,亦即最初要 最小化的量。
因此,在要求约束条件得到满足的情况下最小化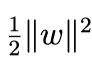 ,实际上等价于直接最小化 θ(w)(当然, 这里也有约束条件, 就是 α i ≥ 0, i = 1, …, n),因为如果约束条件没有得 到满足, θ(w) 会等于无穷大,自然不会是我们所要求的最小值。
,实际上等价于直接最小化 θ(w)(当然, 这里也有约束条件, 就是 α i ≥ 0, i = 1, …, n),因为如果约束条件没有得 到满足, θ(w) 会等于无穷大,自然不会是我们所要求的最小值。
具体写出来,目标函数变成了:
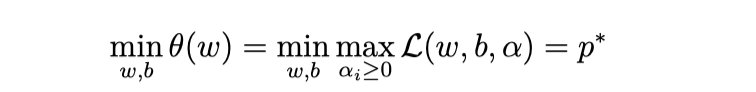
这里用 p* 表示这个问题的最优值,且和最初的问题是等价的。如果直接求解,那么一上来便得面对 w 和 b 两个参数,而 α i 又是不等式约束,这个求解过程不好做。
此时,我们可以借助对偶问题进行求解。
3.2.2 对偶问题
因为我们在上面求解的过程中,直接求解 w 和 b 两个参数不方便,所以想办法转换为对偶问题。
我们要将其转换为对偶问题,变成极大极小值问题:
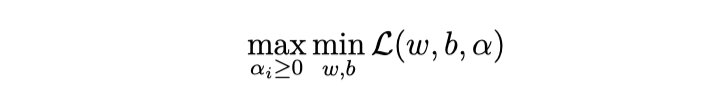
参考资料: https://wenku.baidu.com/view/7bf945361b37f111f18583d049649b6649d70975.html
如何获取对偶函数?
-
首先我们对原目标函数的w和b分别求导:
- 原目标函数:
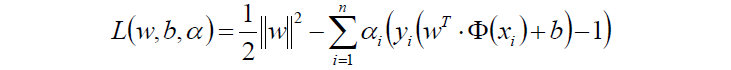
- 对w求偏导:
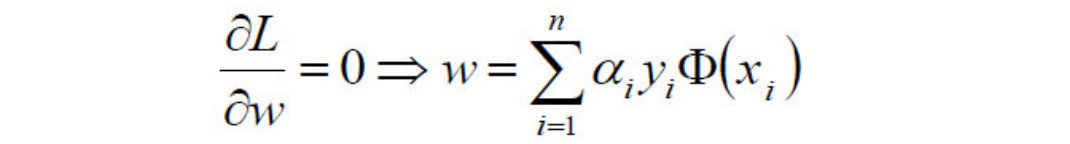
- 对b求偏导:
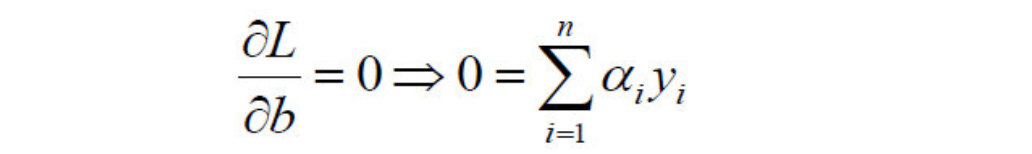
- 原目标函数:
-
然后将以上w和b的求导函数重新代入原目标函数的w和b中,得到的就是原函数的对偶函数:
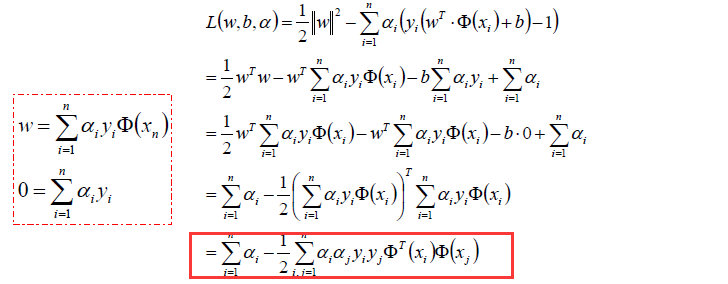
- 这个对偶函数其实求的是:
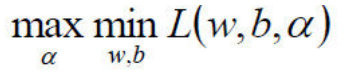 中的minL(w,b)min**L(w,b)部分(因为对w,b求了偏导)。
中的minL(w,b)min**L(w,b)部分(因为对w,b求了偏导)。 - 于是现在要求的是这个函数的极大值max(a),写成公式就是:
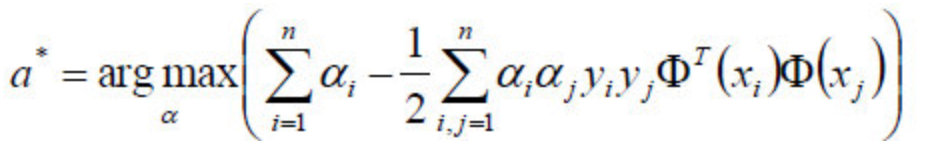
- 好了,现在我们只需要对上式求出极大值α,然后将α代入w求偏导的那个公式:
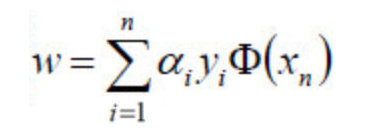
- 从而求出w.
- 将w代入超平面的表达式,计算b值;
- 现在的w,b就是我们要寻找的最优超平面的参数。
3.2.3 整体流程确定
我们用数学表达式来说明上面的过程:
- 1)首先是求
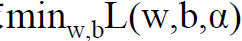 的极大值。即:
的极大值。即:
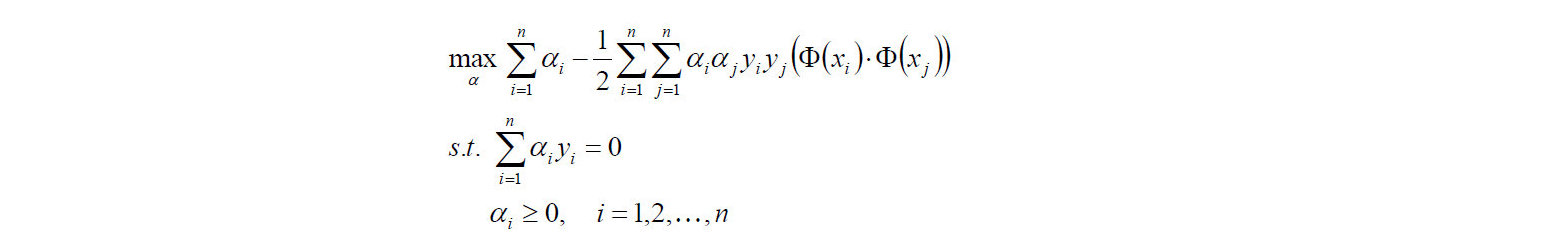
注意有两个约束条件。
- 对目标函数添加负号,转换成求极小值:
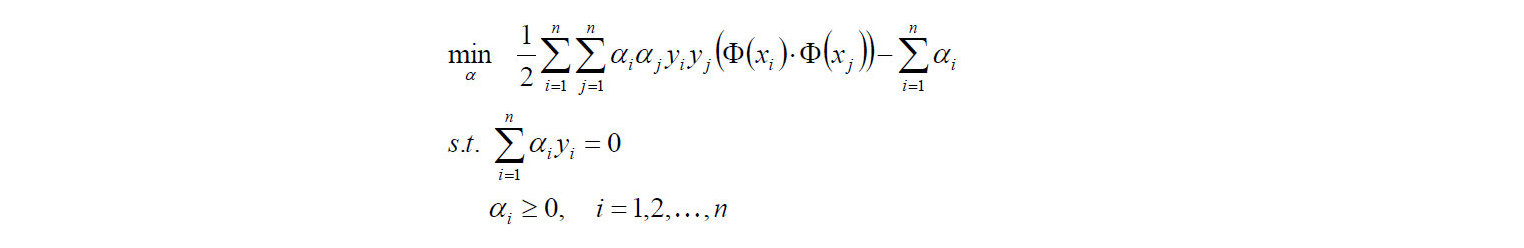
- 2)计算上面式子的极值求出 α*;
- 3)α* 代入,计算w,b
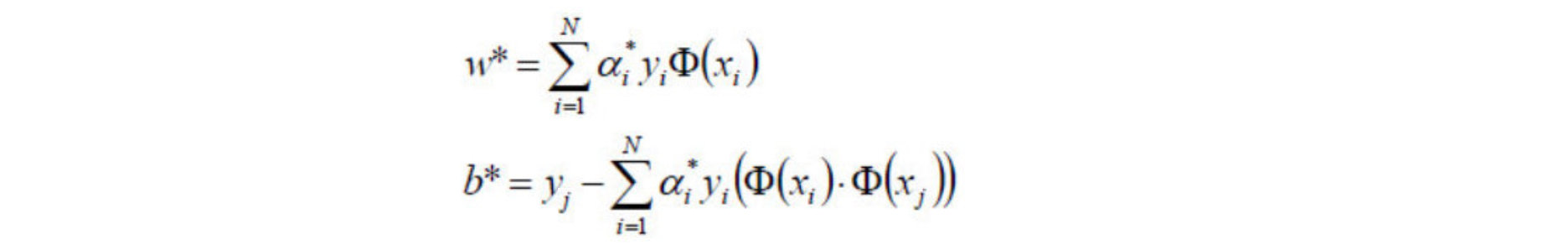
- 4)求得超平面:
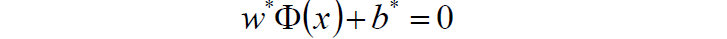
- 5)求得分类决策函数:
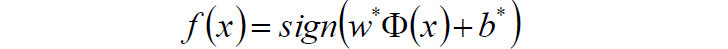
4 举例
给定3个数据点:正例点x1=(3,3),x2=(4,3),负例点x3=(1,1),求线性可分支持向量机。 三个点画出来:
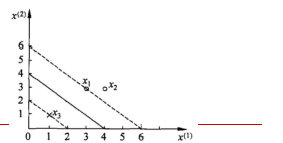
- 首先确定目标函数
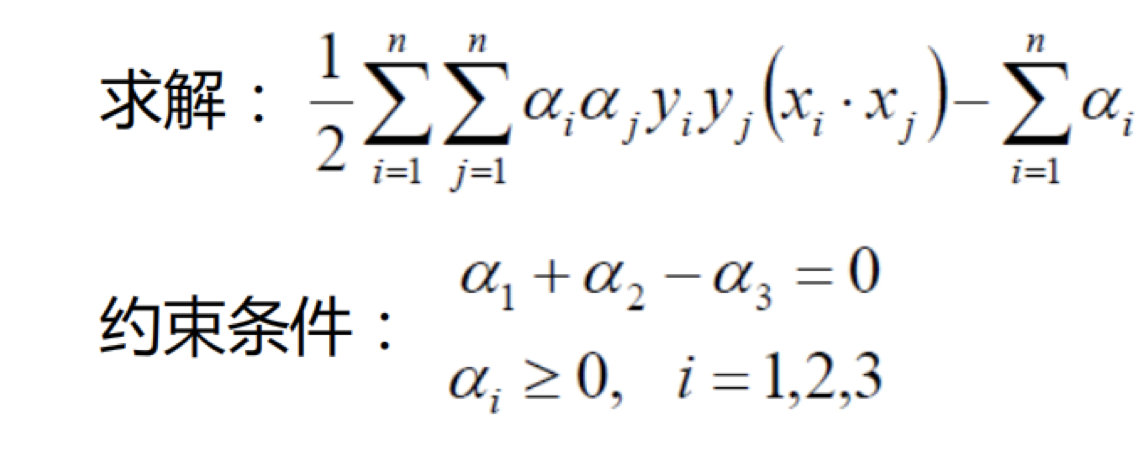
- 求得目标函数的极值
- 原式:
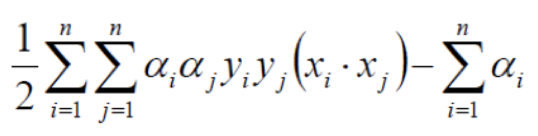
- 把数据代入:
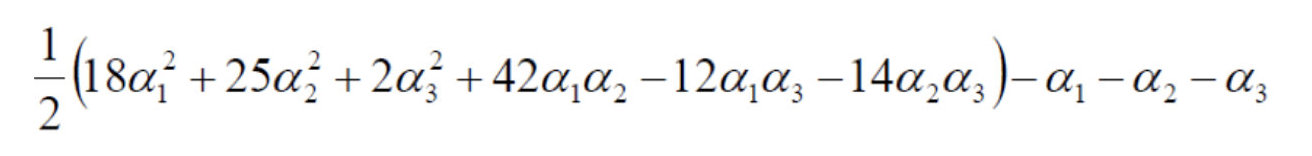
- 由于:
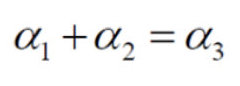
- 化简可得:
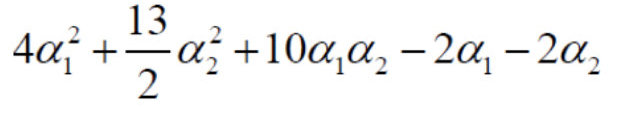
- 对α1,α2 求偏导并令其为0,易知s(α1, α2)在点(1.5, -1)处取极值。
- 而该点不满足条件α2 >= 0,所以,最小值在边界上达到。
- 当α1=0 时,最小值s(0,\frac{2}{13})=-\frac{2}{13}=-0.1538s(0,132)=−132=−0.1538
- 当α2=0 时,最小值s(\frac{1}{4},0)=-\frac{1}{4}=-0.25s(41,0)=−41=−0.25
- 于是,s(α1, α2)在α1=1/4 , α2=0时达到最小,此时:\alpha_3 = \alpha_1+\alpha_2 = \frac{1}{4}α3=α1+α2=41
- 将求得的极值代入从而求得最优参数w,b
-
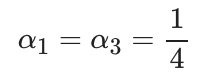 对应的点x1, x3就是支持向量机
对应的点x1, x3就是支持向量机 -
代入公式:
-
将α结果代入求解:
-
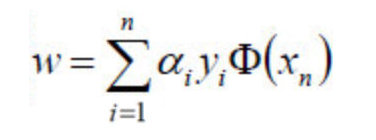
-
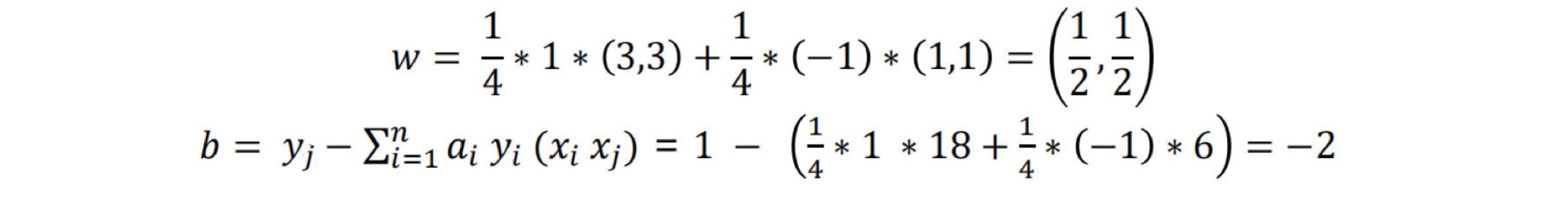
选择α的一个支持向量的正分量αj>0进行计算
-
平面方程为:0.5x_1+0.5x_2-2=00.5x1+0.5x2−2=0
-
-
因此得到分离超平面为: 0.5x_1+0.5x_2-2=00.5x1+0.5x2−2=0
-
得到分离决策函数为:f(x)=sign(0.5x_1+0.5x_2-2)f(x)=sig**n(0.5x1+0.5x2−2)
ps:参考的另一种计算方式: https://blog.csdn.net/zhizhjiaodelaoshu/article/details/97112073
5 小结
-
SVM中目标函数
-
SVM中目标函数的求解过程
-
1)首先是求
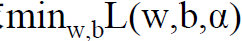 的极大值。即:
的极大值。即: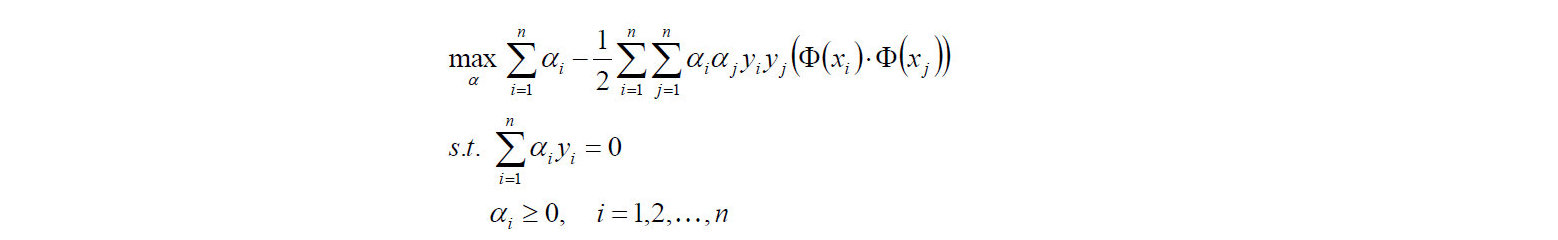
注意有两个约束条件。
-
对目标函数添加符号,转换成求极小值:
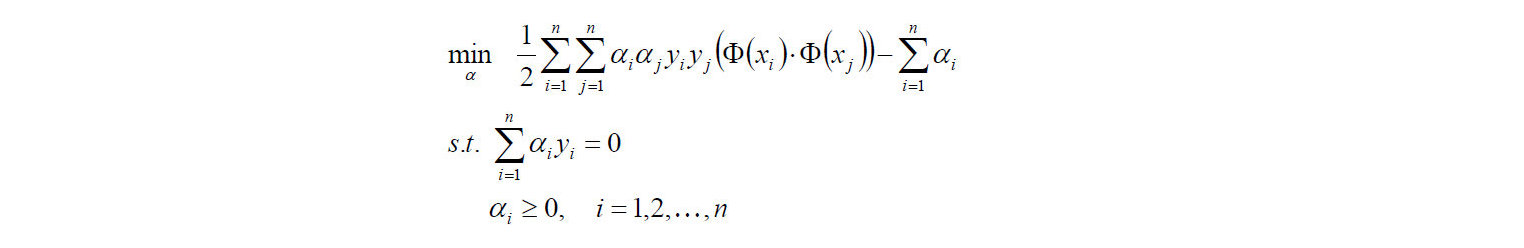
-
2)计算上面式子的极值求出α*;
-
3)将α*代入,计算w,b
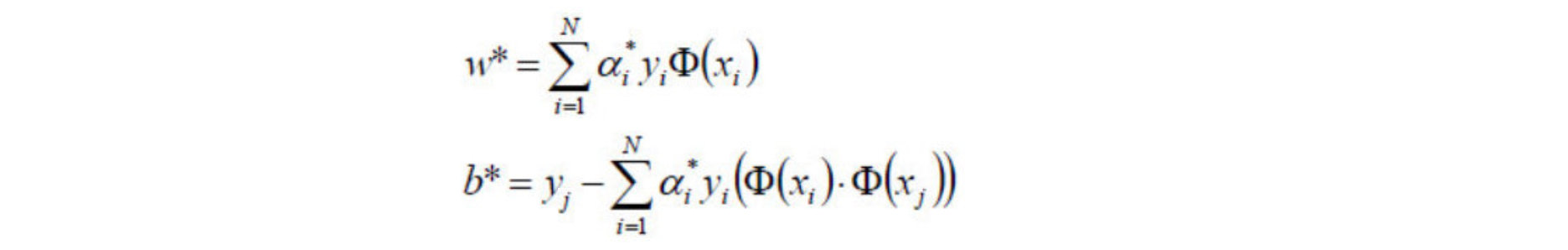
-
4)求得超平面:
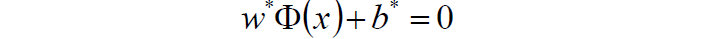
-
5)求得分类决策函数:
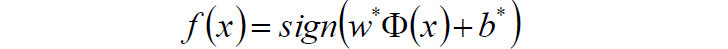
-