最小生成树-Prim + Kruskal算法
目录
- 一、 最小生成树定义及相关约定
- 1. 定义
- 2. 约定
- 二、最小生成树原理
- 1. 数的性质
- 2. 切分定理
- 3. 贪心算法
- 三、Prim算法
- 1. Prim算法流程
- 2. Prim算法实现
- 3. Prim算法实现精简版
- 四、Kruskal算法
- 1. Kruskal算法流程
- 2. Kruskal算法实现
- 3. Kruskal算法实现精简版
一、 最小生成树定义及相关约定
在加权图中,它的边关联了一个权重,那么我们就可以根据这个权重解决最小成本问题,但如何才能找到最小成本对应的顶点和边呢?最小生成树相关算法可以解决。
1. 定义
图的生成树是它的一棵含有其所有顶点的无环连通子图,一副加权无向图的最小生成树它的一棵权值(树中所有边的权重之和)最小的生成树
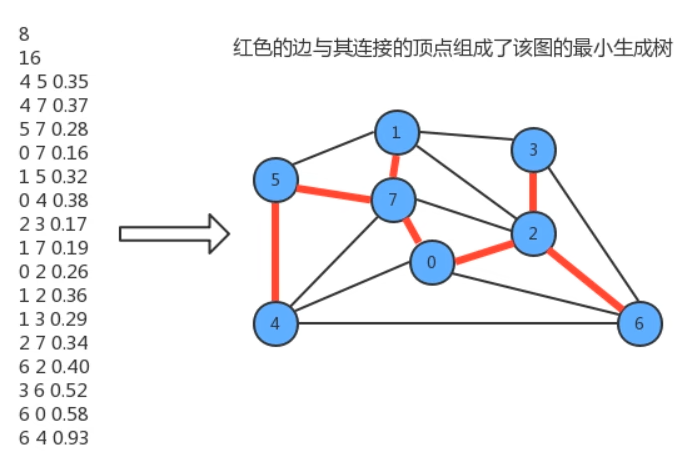
2. 约定
只考虑连通图。最小生成树的定义说明它只能存在于连通图中,如果图不是连通的,那么分别计算每个连通图子图的最小生成树,合并到一起称为最小生成森林。
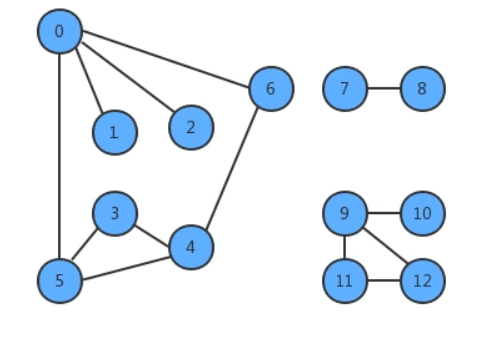
二、最小生成树原理
1. 数的性质
- 用一条边接树中的任意两个顶点都会产生一个新的环
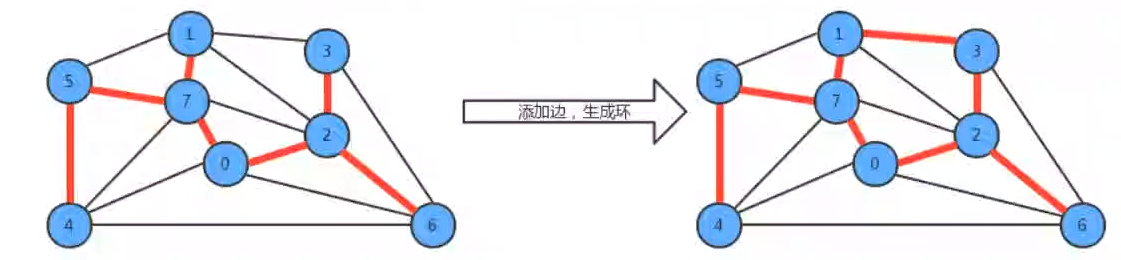
- 从树中删除任意一条边,将会得到两棵独立的树
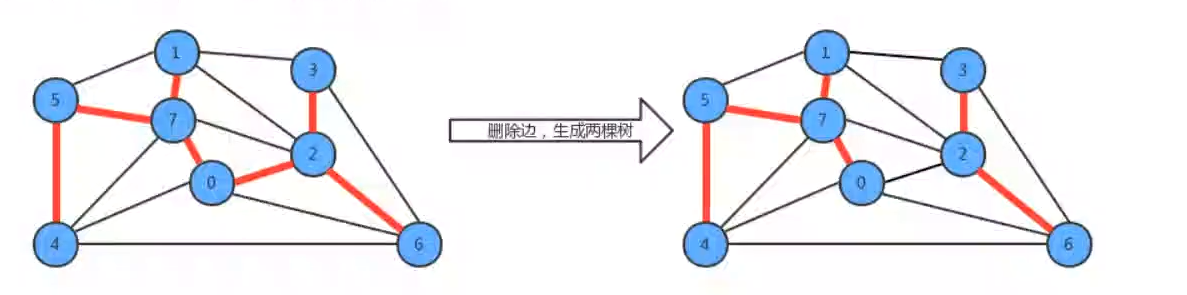
2. 切分定理
要从一副连通图中找出该图的最小生成树,需要通过切分定理完成。
切分
将图的所有顶点按照某些规则分为两个非空且没有交集的集合。
横切边
连接两个属于不同集合的顶点的边称之为横切边。
例如我们将图中的顶点切分为两个集合,灰色顶点属于一个集合,白色顶点属于另外一个集合,那么效果如下:
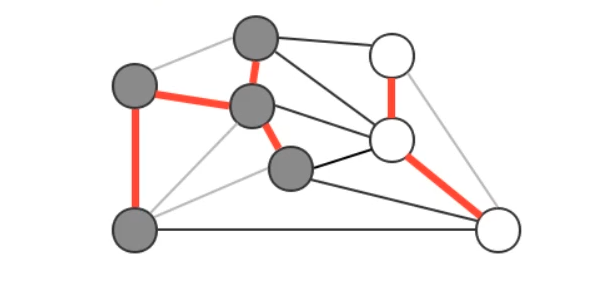
切分定理
在一副加权图中,给定任意的切分,它的横切边中的权重最小者必然属于图中的最小生成树。
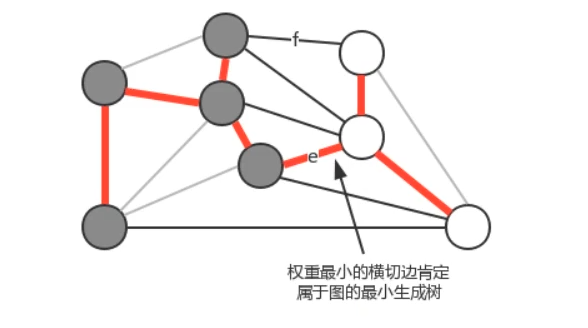
注意:一次切分产生的多个横切边中,权重最小的边不一定是所有横切边中唯一属于图的最小生成树的边。
3. 贪心算法
贪心算法是计算图的最小生成树的基础算法,它的基本原理就是切分定理,使用切分定理找到最小生成树的一条边,不断的重复直到找到最小生成树的所有边。如果图有V个顶点,那么需要找到V - 1条边,就可以表示该图的最小生成树。
计算图的最小生成树的算法有很多种,但这些算法都可以看做是贪心算法的一种特殊情况,这些算法的不同之处在于保存切分和判定权重最小的横切边的方式。
三、Prim算法
Prim算法,它的每一步都会为一棵生成中的树添加一条边。一开始这棵树只有一个顶点,然后会向它添加V - 1条边,每次总是将下一条连接树中的顶点与不在树中的顶点且权重最小的边加入到树中。
Prim算法的切分规则
把最小生成树中的顶点看做是一个集合,把不在最小生成树中的顶点看做是另外一个集合。

1. Prim算法流程
Prim算法始终将图中的顶点切分成两个集合,最小生成树顶点和非最小生成树顶点,通过不断的重复做某些操作,可以逐渐将非最小生成树中的顶点加入到最小生成树中,直到所有的顶点都加入到最小生成树中。
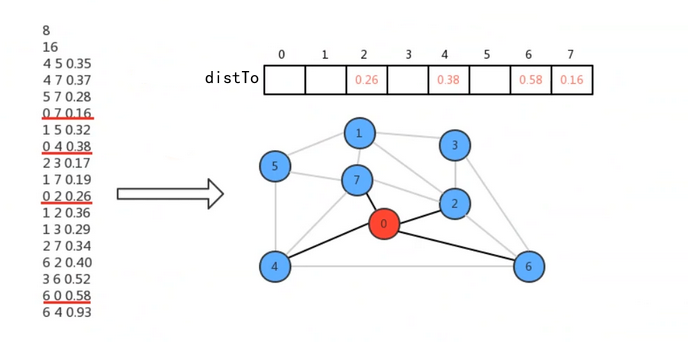
2. Prim算法实现
代码中提到的Edge、EdgeWeightedGraph 类可详见Java数据结构-图
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.PriorityQueue;
public class PrimMST {
// 索引代表顶点,值表示当前顶点和最小生成树之间的最短边
private Edge[] edgeTo;
// 索引代表顶点,值表示当前顶点和最小生成树之间的最短边的权重
private double[] distTo;
// 索引代表顶点,如果当前顶点已经在生成树中,则值为true,否则为false
private boolean[] marked;
/*
存放树中顶点与非树中顶点之间的有效横切边
使用优先队列,Edge实现了 Comparable
每次返回权重最小的边
*/
private PriorityQueue<Edge> pq;
// 根据一副加权无向图,创建最小生成树计算对象
public PrimMST(EdgeWeightedGraph G) {
// 初始化edgeTo
this.edgeTo = new Edge[G.V()];
// 初始化distTo
this.distTo = new double[G.V()];
Arrays.fill(distTo, Double.POSITIVE_INFINITY);
// 初始化marked
this.marked = new boolean[G.V()];
// 初始化pq
pq = new PriorityQueue<Edge>(G.V());
visit(G, 0);
//遍历索引最小优先队列,拿到最小和N切边对应的顶点,把该顶点加入到最小生成树中
while (!pq.isEmpty()){
// 取出当前距离生成树权重最小的边
Edge e = pq.poll();
// 获取两个顶点的索引
int v = e.either(), w = e.other(v);
// 如果两个点现在均已加入了生成树,则不做处理
if (marked[v] && marked[w])
continue;
// 当前 v 点未加入
if (!marked[v])
visit(G, v);
// 当前 w 点未加入
if (!marked[w])
visit(G, w);
}
}
// 将顶点v添加到最小生成树中,并且更新数据
private void visit(EdgeWeightedGraph G, int v) {
// 把顶点v添加到最小生成树中
marked[v] = true;
// 更新数据
for (Edge e : G.adj(v)) {
// 获取e边的另外一个顶点(当前顶点是v)
int w = e.other(v);
/*
判断另外一个顶点是不是已经在生成树中,
如果在树中,则不做任何处理,如果不在树中,更新数据
*/
if (marked[w]){
continue;
}
// 判断边e的权重是否小于从w顶点到树中已经存在的最小边的权重;
if (e.weight() < distTo[w]){
// 更新数据
edgeTo[w] = e;
distTo[w] = e.weight();
pq.offer(e);
}
}
}
// 获取最小生成树的所有边
public List<Edge> edges() {
// 创建队列对象
List<Edge> allEdges = new ArrayList<>();
// 遍历edgeTo数组,拿到每一条边,如果不为null,则添加到列表中
for (Edge edge : edgeTo) {
if (edge != null) {
allEdges.add(edge);
}
}
return allEdges;
}
}
3. Prim算法实现精简版
上述算是Prim算法的标准版,但如果对于解决一些小算法题,设计边、加权有向图类,在代码中还是比较臃肿,以下实现一个Prim算法的精简版,使用邻接矩阵来存储图。
public class PrimMST {
// 图类
static class Graph{
// 顶点数量
int v;
// 使用邻接矩阵存放边,weights[i][j] 代表 i -> j 的权重
double[][] weights;
public Graph(int v, double[][] weights) {
this.v = v;
this.weights = weights;
}
}
/*
根据传入的图,计算最下生成树的权重;
若不存在生成树,返回 -1
*/
public static double prim(Graph graph){
// 标记已加入最小生成树的顶点
int[] visited = new int[graph.v];
// 标记每个顶点到生成树的最短距离
double[] distTo = new double[graph.v];
// 所有点到生成树的距离都设为正无穷
Arrays.fill(distTo, Double.MAX_VALUE);
/*
等会遍历时会从 0 作为起始点, 0 号一定会加入生成树,
所以赋值它到生成树的距离为 0
*/
distTo[0] = 0;
double sumWeight = 0;
// 遍历 graph.v 次
for (int k = 0; k < graph.v; ++k){
// 找到目前距离生成树距离最小的顶点的索引
int tempIndex = -1;
for (int i = 0; i < graph.v; ++i) {
if (visited[i] == 0 && (tempIndex == -1 || distTo[i] < distTo[tempIndex])) {
tempIndex = i;
}
}
if (k != 0 && distTo[tempIndex] == Double.MAX_VALUE){
/*
当前点不为起始点并且距离生成树的距离已为正无穷,说明图已经不连通了,
不存在生成树,直接返回 -1
*/
return -1;
}
// 将该点到生成树的距离加入总权重
sumWeight += distTo[tempIndex];
// 标记该点已经加入生成树
visited[tempIndex] = 1;
for (int j = 0; j < graph.v; ++j){
/*
用以上加入生成树的点更新其他点到生成树的距离
主要是解决 tempIndex 点的连接点
这可以比喻为 tempIndex 处的顶点当上了驸马加入了皇家
那么跟他有关系的顶点距离皇家的距离也更近了
*/
distTo[j] = Math.min(distTo[j], graph.weights[tempIndex][j]);
}
}
return sumWeight;
}
}
四、Kruskal算法
kruskal算法是计算一副加权无向图的最小生成树的另外一种算法,它的主要思想是按照边的权重(从小到大)处理它们,将边加入最小生成树中,加入的边不会与已经加入最小生成树的边构成环,直到树中含有V - 1条边为止。
kruskal算法和prim算法的区别:
Prim算法是一条边一条边的构造最小生成树,每一步都为一棵树添加一条边。kruskal算法构造最小生成树的时候也是一条边一条边地构造,但它的切分规则是不一样的。它每一次寻找的边会连接一片森林中的两棵树。如果一副加权无向图由V个顶点组成,初始化情况下每个顶点都构成一棵独立的树,则V个顶点对应V棵树,组成一片森林,
kruskal算法每一次处理都会将两棵树合并为一棵树,直到整个森林中只剩一棵树为止。
1. Kruskal算法流程
初始化先将所有边加入优先队列,每次使用poll()取出权重最小的边,并得到该边关联的两个顶点v和w,通过uf.connect(v, w)判断v和w是否已经连通,如果连通,则证明这两个顶点在同一棵树中,那么就不能再把这条边添加到最小生成树中,因为在一棵树的任意两个顶点上添加一条边,都会形成环,而最小生成树不能有环的存在,如果不连通,则通过uf.union(v, w)把顶点v所在的树和顶点w所在的树合并成一棵树,并把这条边加入到mst列表中,这样如果把所有的边处理完,最终mst中存储的就是最小生树的所有边。
2. Kruskal算法实现
同样的,代码中提到的Edge、EdgeWeightedGraph 类可详见Java数据结构-图
同时,在这里还使用了另外一个数据结构-并查集,可详见Java数据结构-并查集
import java.util.ArrayList;
import java.util.List;
import java.util.PriorityQueue;
public class KruskalMST {
// 保存最小生成树的所有边
private List<Edge> mst;
/*
索引代表顶点,使用uf.connect(v,w)可以判断顶点v和顶点w是否在同一颗树中,
使用uf.union(v,w)可以把顶点v所在的树和顶点w所在的树合并
*/
private UF_Tree_Weighted uf;
// 存储图中所有的边,使用优先队列,对边按照权重进行排序
private PriorityQueue<Edge> pq;
// 根据一副加权无向图,创建最小生成树计算对象
public KruskalMST(EdgeWeightedGraph G) {
// 初始化mst
this.mst = new ArrayList<>();
// 初始化uf
this.uf = new UF_Tree_Weighted(G.V());
// 初始化 pq
this.pq = new PriorityQueue<>();
// 把图中所有的边存储到pq中
for (Edge e : G.edges()) {
pq.offer(e);
}
// 遍历pq队列,拿到最小权重的边,进行处理
while(!pq.isEmpty() && mst.size() < G.V() - 1){
// 找到权重最小的边
Edge e = pq.poll();
// 找到该边的两个顶点
int v = e.either();
int w = e.other(v);
/*
判断这两个顶点是否已经在同一颗树中,
如果在同一颗树中,则不对该边做处理,
如果不在一棵树中,则让这两个顶点属于的两棵树合并成一棵树
*/
if (uf.connected(v, w)){
continue;
}
uf.union(v,w);
// 让边e进入到mst队列中
mst.add(e);
}
}
// 获取最小生成树的所有边
public List<Edge> edges() {
return mst;
}
}
3. Kruskal算法实现精简版
在三中我们使用了Prim算法的精简版,同样的,上述算是kruskal算法的标准版,但如果对于解决一些小算法题,设计边、加权有向图类、以及并查集,在代码中还是比较臃肿,以下实现一个kruskal算法的精简版,使用邻接矩阵来存储图。
public class KruskalMST {
// 图类
static class Graph{
// 顶点数量
int v;
// 使用邻接矩阵存放边,weights[i][j] 代表 i -> j 的权重
double[][] weights;
/*
存放边的信息
way[i][0] way[i][1] way[i][2]
分别代表 第 i 条边的起点、终点、权重
用 Number 类是因为 索引为整数 但是权重为小数
*/
List<Number[]> way;
public Graph(int v, double[][] weights) {
this.v = v;
this.weights = weights;
this.way = new ArrayList<>();
for (int i = 0; i < weights.length; ++i){
for (int j = 0; j < weights[i].length; ++j){
/*
因为是无向图,一条边就有两种形容方式 i -> j 与 j -> i
此处只取一种
*/
if (weights[i][j] != Double.MAX_VALUE && i < j)
way.add(new Number[]{i, j, weights[i][j]});
}
}
// 按照权重排序,(这就类似上述使用的优先队列了)
Collections.sort(way, new Comparator<Number[]>() {
@Override
public int compare(Number[] o1, Number[] o2) {
double r = (double)o1[2] - (double) o2[2];
return r < 0 ? -1 : r > 0 ? 1 : 0;
}
});
}
}
// 将 a, b 归为一组
public static void connection(int[] groups, int a, int b){
int gA = groups[a];
int gB = groups[b];
// 全部化为 gA 的 值
for (int i = 0; i < groups.length; ++i){
if (groups[i] == gB)
groups[i] = gA;
}
}
// 返回 a 所在分组
public static int find(int[] groups, int a){
return groups[a];
}
/*
根据传入的图,计算最下生成树的权重;
若不存在生成树,返回 -1
*/
public static double kruskal(Graph graph){
// 建立 并查集
int[] groups = new int[graph.v];
for (int i = 0; i < groups.length; ++i)
groups[i] = i;
// 统计待会找到的边数
int countE = 0;
double sumWeight = 0;
for (int i = 0; i < graph.way.size(); ++i){
// 获取边的 起点、终点、权值
int a = (int) graph.way.get(i)[0];
int b = (int) graph.way.get(i)[1];
double w = (double) graph.way.get(i)[2];
int gA = find(groups, a);
int gB = find(groups, b);
if (gA != gB){
// 若 a、b 不属于同一组,则将他们分为同一组
connection(groups, a, b);
sumWeight += w;
countE += 1;
}
}
// 找到的边的数量不为 结点数 - 1, 不存在生成树
if (countE < graph.v - 1)
return -1;
return sumWeight;
}
}
