数据结构与算法(java版)第二季 - 4 快速、希尔排序(未完)
目录
快速排序(Quick Sort)
希尔排序(Shell Sort)
快速排序(Quick Sort)

快速排序 – 执行流程
①从序列中选择一个轴点元素(pivot)
✓ 假设每次选择0位置的元素为轴点元素

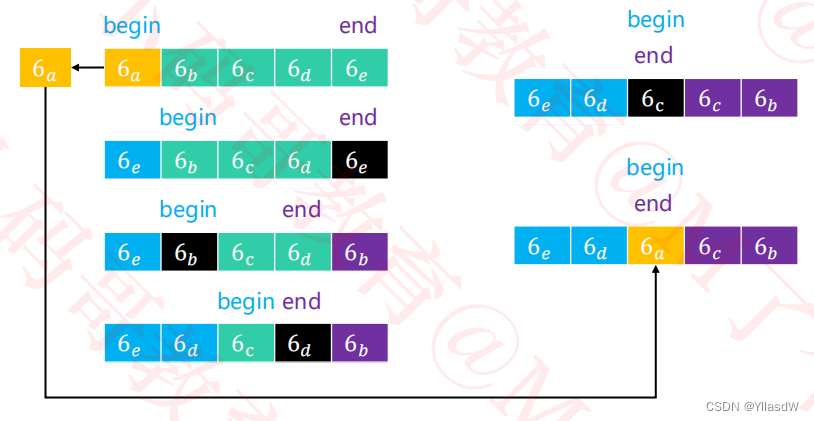
上述的扫描过程:
①首先将6a进行一个备份;
②首先将end-1,扫描到7,其大于6,将end--;
③发现end的这个位置的数字是比原来的6a小的,将5覆盖掉原来的begin位置,在这个时候将begin进行一个++操作;
依次进行上述的操作,注意:这里我们将两个相同的元素之中,将一样的元素看成是比原来的元素小的,为什么这样做呢?后面会说到的。
从左往右进行扫描,如果要是扫描到比轴点坐标小于等于的,则不发生改变,要是扫描到比轴点大,那么就是会发生一个位置的调换。同理,从右往左进行相应的扫描。
代码如下所示:
package com.mj.sort.cmp;
import com.mj.sort.Sort;
public class QuickSort1<T extends Comparable<T>> extends Sort<T> {
@Override
protected void sort() {
sort(0, array.length);
}
/*
对于[begin,end)之中的元素进行相应的
*/
private void sort(int begin, int end) {
if (end - begin < 2) return;
// 确定轴点位置 O(n)
int mid = pivotIndex(begin, end);
// 对子序列进行快速排序
sort(begin, mid);
sort(mid + 1, end);
}
/**
* 构造出 [begin, end) 范围的轴点元素
*
* @return 轴点元素的最终位置
*/
private int pivotIndex(int begin, int end) {
// 随机选择一个元素跟begin位置进行交换
swap(begin, begin + (int) (Math.random() * (end - begin)));
// 备份begin位置的元素---这里就是在图示之中的6a
T pivot = array[begin];
// end指向最后一个元素---将最后的一个位置进行--操作
end--;
//下面是两种操作,分情况进行讨论
while (begin < end) {
while (begin < end) {
if (cmp(pivot, array[end]) < 0) { // 右边元素 > 轴点元素
end--;
} else { // 右边元素 <= 轴点元素 右边的元素是小于或者等于轴点的大小的时候,将右边的值之间进行覆盖掉左边的begin位置的值
array[begin++] = array[end];
break;
}
}
//下面是进行掉头的一段代码,使用的是进行掉头的方式.
while (begin < end) {
if (cmp(pivot, array[begin]) > 0) { // 左边元素 < 轴点元素
begin++;
} else { // 左边元素 >= 轴点元素
array[end--] = array[begin];
break;
}
}
}
//使用备份的轴点元素放入到最终的位置之中
array[begin] = pivot;
//返回轴点元素
return begin;
}
}

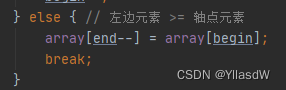
进行掉头换方向,为什么要这么做呢?
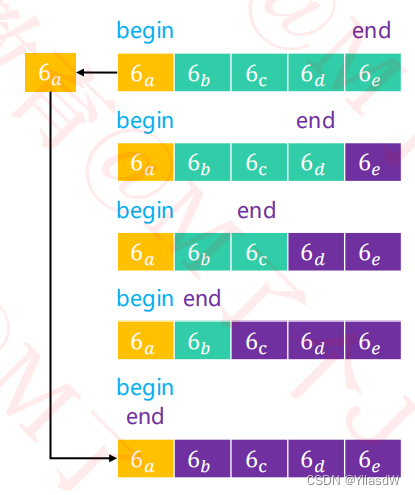
最坏情况的出现,使得相应的使用了五次的轴点过程,是非常麻烦的.
 我们在使用这种方式之后是仍然能够做到相应的平均分割的过程实现,为了避免出现下面的最坏的情况出现,什么是所谓的最坏情况,下面是进行了相应的解释.
我们在使用这种方式之后是仍然能够做到相应的平均分割的过程实现,为了避免出现下面的最坏的情况出现,什么是所谓的最坏情况,下面是进行了相应的解释.
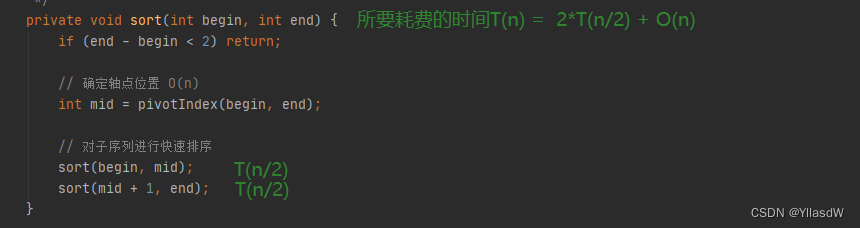
为什么这里的复杂度是相应的nlog(n)见下面的递推式与复杂度关系
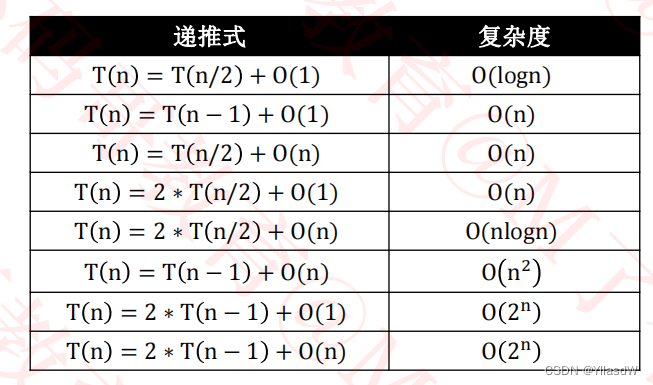
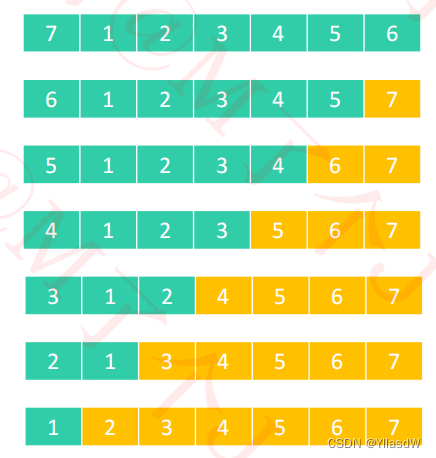
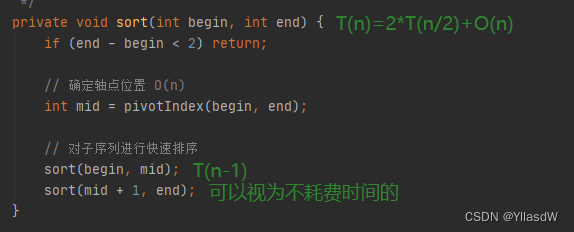
T (n) = T (n − 1) + O (n) = O(n^2)极其不均匀的情况出现
为了避免上面的情况的出现,使用随机选择元素的方式作为轴点元素,只是需要将最初的位置之中的代码进行相应的交换过程.
这里的Math.random()是不包含1的----[0,1)
上面的不均匀过程极端等情况的出现可能会导致在这里栈溢出的问题,如果要是尽量让他在栈溢出的范围以内.
希尔排序(Shell Sort)
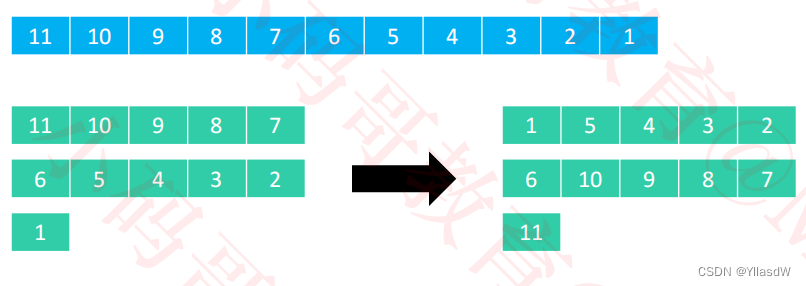
希尔排序的例子[看了很长时间,没看懂,后面补上]
栗子一:
①将上面的序列分成八列进行排序

这个地方没有懂,但是知道这个过程就是可以的,后面依次类推
②分成四列进行排序
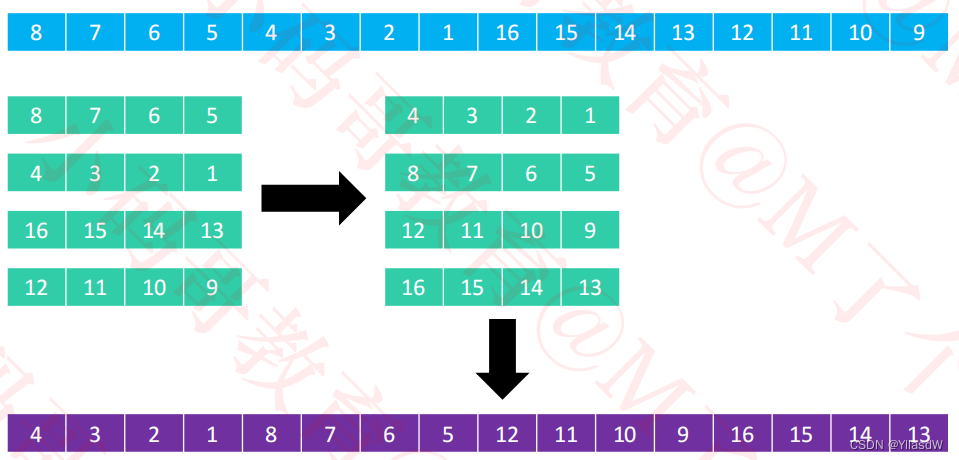
③分成两列进行排序
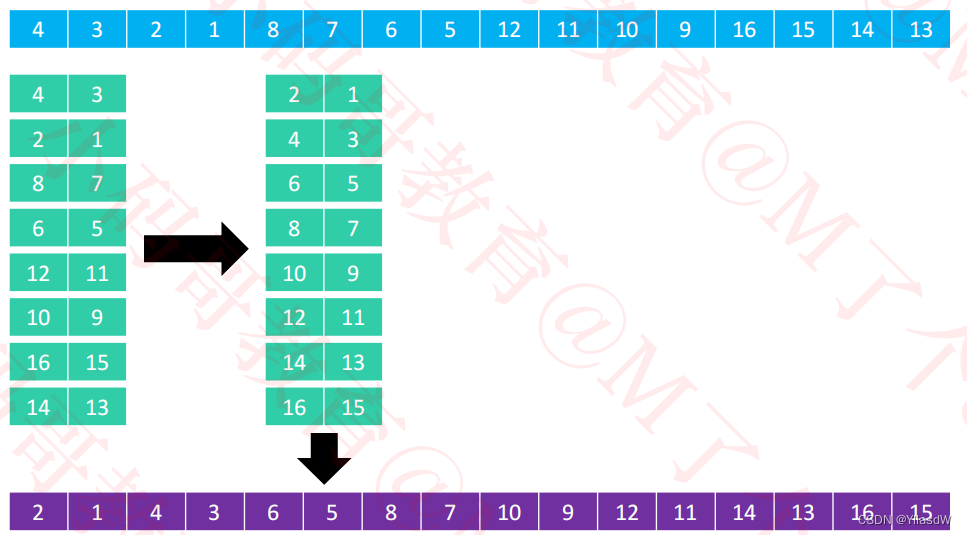
④分成一列进行排序
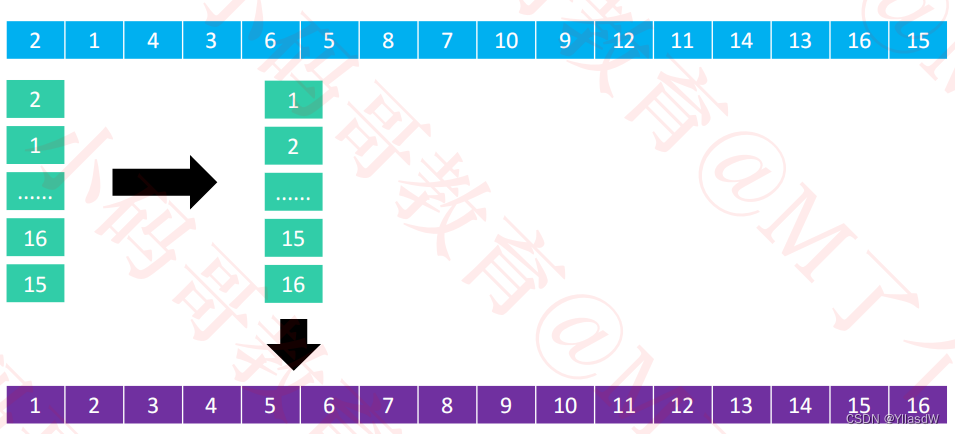 问:为什么一开始直接分成一列不就好了吗?
问:为什么一开始直接分成一列不就好了吗?
①直接分成一列是没有意义的,那干脆就不要分了[老师原话].
②上面的过程之中,从八列变成一列的过程之中,逆序对是越来越少的.[前面是有意义的]
③并且希尔排序底层一般使用插入排序对每一列进行排序,也很多资料认为希尔排序是插入排序的改进版
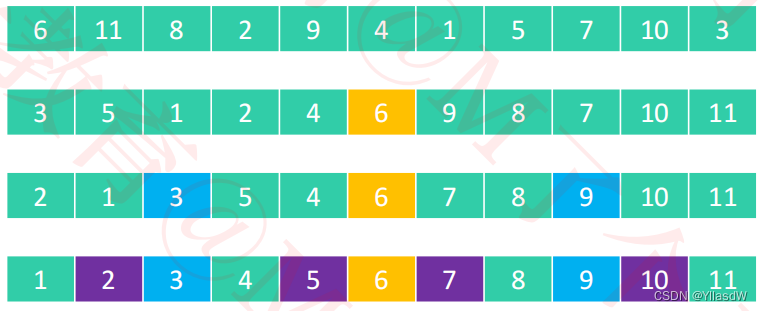
栗子二:
假设是存在相应的11个元素的,步长序列是{1,2,5}