粒子群算法PSO求解最大值和最小值案例(超详细注释)
目录
前言
1.粒子群算法简介和难点理解
1.1概念理解
①非劣解集和支配
②个体极值和群体极值
③个体适应度值和群体适应度值
1.2 算法流程和理解
1.3 速度和位置更新公式
1.4 rand、randn、rands、randi函数说明
2. 粒子群算法求解最大值问题
2.1 常数惯性权重因子求解最大值问题
2.1.1最优个体适应度计算
2.2 线性递减惯性权重因子求解最大值问题
2.3 非线性递减惯性权重因子形①求解最大值问题
2.4 非线性递减惯性权重因子形②求解最大值问题
2.5 非线性递减惯性权重因子形③求解最大值问题
2.6 非线性递减惯性权重因子形④求解最大值问题
2.7 汇总对比
3. 粒子群算法求解最小值问题
4.总结
前言
上篇文章详细介绍了常规遗传算法、遗传算法封装库函数ga和gamultiobj,以及optimtool工具箱的使用,这篇文章将介绍常规粒子群算法、例子全封装库函数particleswarm,以及如何结合粒子群算法和simulink联合仿真优化PID。
1.粒子群算法简介和难点理解
1.1概念理解
在这里解释一下几个概念:
①非劣解集和支配
非劣解集可以理解等价于支配,其实就是最优解的意思
②个体极值和群体极值
个体极值指的是所有个体寻优自变量x解的集合,指的是所有粒子/个体;群体极值指的是种群中的最优自变量解,指的是一个粒子。即指的是目标函数自变量的取值。
③个体适应度值和群体适应度值
个体适应度值指的是所有个体寻优目标函数解xfval的集合,指的是所有粒子/个体;群体适应度值指的是种群中的最优解xfval,指的是一个粒子。即指的是目标函数xfval的取值。
1.2 算法流程和理解

粒子群寻优的算法流程
可以这样理解PSO:有一群鸟去寻找食物,其目的在于找到食物最多的地方,然后再大家一起去那里定居,但是每只鸟都会找到自己认为食物最多的地方,这个就叫做局部最优;为了防止陷入局部最优,所以大家定期会聚集在一起讨论,并进行食物量多少的比较,最终找到食物最多的地方,便是全局最优解。
为了方便让大家理解,这里展示同一个多峰函数求解最大值和最小值的问题,而两个代码之间做一些稍微的修改即可转换。
另外这里推荐大家可以参照这个b站up的视频进行学习,因为毕竟有人觉得看文字费劲,可以先看视频再来结合本篇文章进行阅读,b站视频链接:
【粒子群优化算法】手把手带你编写粒子群优化算法的matlab代码_哔哩哔哩_bilibili
1.3 速度和位置更新公式


1.4 rand、randn、rands、randi函数说明
rand(m,n) : 在 ( 0~1 ) 内生成m行n列均匀分布的伪随机数矩阵;
randn (m,n) : 生成m行n列标准正态分布 ( 均值为0,方差为1 ) 的伪随机数矩阵;
rands(m,n) : 在 ( -1~1 ) 内生成m行n列均匀分布的伪随机数;
randi( [min,max] , m , n) : 在 [min,max] 内生成m行n列的均匀分布的随机整数矩阵;
2. 粒子群算法求解最大值问题
问题:

x和y取值均为[-2 2],求该非线性函数的最大值。
2.1 常数惯性权重因子求解最大值问题
2.1.1最优个体适应度计算
最优个体适应度应该 = 种群中后一代粒子适应度值/前一代粒子适应度值
或者说有k个这样种群同时进化,最优个体适应度应该 =每个种群个体适应度值总和/k
实现程序:
适应度函数:
function y = myfitness1(x)
%x 输入粒子的位置
%y 输出粒子适应度值
y=-(sin( sqrt(x(1).^2+x(2).^2) )./sqrt(x(1).^2+x(2).^2)+exp((cos(2*pi*x(1))+cos(2*pi*x(2)))/2)-2.71289);
主程序:
clc
clear
%% 参数初始化
c1 = 2;c2 = 2;%速度更新参数
maxgen = 300;%迭代次数
sizepop = 20;%粒子数量/种群大小
Vmax = 0.5;Vmin = -0.5;%粒子的最大和最小速度,这个可以根据自己的需求定义
popmax = 2;popmin = -2;%粒子的最大和最小位置,即x的取值范围,或者说是粒子的搜索范围
dim = 2;%维度,可以理解为自变量数
ws = 0.9;%初始惯性权重
we = 0.4;%迭代至最大次数时的惯性权重
%% 开始100次试验
for g =1:100 %假设有100个这样的种群同时在进化/或者说这个种群重复100次进化
%% 随机初始化粒子速度和粒子位置(先速度后位置),并根据适应度函数计算粒子适应度值
g %第g次试验
for i = 1:sizepop %20个粒子,每个都要初始化
%随机产生一个种群
pop(i,:) = 2*rands(1,dim);%将粒子位置都随机分布在-2~2之间
V(i,:) = 0.5*rands(1,dim);%将粒子速度都随机分布在-0.5~0.5之间
%计算粒子/个体适应度值
fitness(i) = myfitness1(pop(i,:));%将粒子位置代入适应度函数(这里2个变量/2维),求解出粒子适应度值
end
%% 寻找初值个体极值和群体极值,用于后续迭代过程
[bestfitness,bestindex] = max(fitness);
gbest = pop;%因为是初始时刻,所以个体极值位置/所有粒子最好位置的集合,就是初始时刻粒子位置的集合
fitnessgbest = fitness;%个体适应度值,即初始时刻(此次迭代)所有个体/粒子位置代入适应度函数得到适应度函数的最大/小取值
zbest = pop(bestindex,:);%群体极值位置,即初始时刻(此次迭代)是群体中最好的那个粒子位置
fitnesszbest = bestfitness;%群体适应度值/群体极值,即初始时刻(此次迭代)是群体中最好粒子位置代入适应度函数得到适应度函数的最大/小取值
%% 迭代寻优
for k = 1:maxgen
%计算惯性权重
% w = 1;%常数惯性权重因子
w = ws*(ws-we)*(maxgen-k)/maxgen;%线性递减惯性权重
% w = ws-(ws-we)*(k/maxgen);%非线性递减惯性权重①
% w = ws-(ws-we)*(k/maxgen)^2;%非线性递减惯性权重②
% w = ws+(ws-we)*(2*k/maxgen-(k/maxgen)^2);%非线性递减惯性权重③
% w = we*(ws/we)^(1/(1+10*k/maxgen));%非线性递减惯性权重④
%粒子位置和速度更新
for i = 1:sizepop
%速度更新
V(i,:) = w*V(i,:)+c1*rand*(gbest(i,:)-pop(i,:))+c2*rand*(zbest-pop(i,:));
flagVub = find(V(i,:) > Vmax);%找出迭代过程中超出最大速度的粒子的列数,这里2维,所以有:
%如果粒子的第一个维度的速度 > Vmax,则find(V(i,:) > Vmax)=[1,0]
%如果粒子的第二个维度方向的速度 > Vmax,则find(V(i,:) > Vmax)=[0,2]
%如果两个维度速度都>Vmax,则为[1,2]
V(i,flagVub) = Vmax;
flagVlb = find(V(i,:) < Vmin);%同理找出迭代过程中小于最小速度粒子的列数
V(i,flagVlb) = Vmin;
%位置更新
pop(i,:) = pop(i,:)+V(i,:);%
flagXub = find(pop(i,:) > popmax);
pop(i,flagXub) = popmax;%同理如果位置某个维度的位置>最大位置,则该次迭代产生的粒子该维度位置=最大位置
flagXlb = find(pop(i,:) < popmin);
pop(i,flagXlb) = popmin;
%产生的新粒子适应度值
fitness(i) = myfitness1(pop(i,:));
end
%个体极值和群体极值更新
for j = 1:sizepop
%个体极值更新
if fitness(j) > fitnessgbest(j)%注:因为个体极值是一维数组,所以要一个索引下标
gbest(j,:) = pop(j,:);
fitnessgbest(j) = fitness(j);
end
%群体极值更新
if fitness(j) > fitnesszbest%注:因为个体极值是一个数,所以不需要索引值
zbest = pop(j,:);
fitnesszbest = fitness(j);
end
end
result(k) = fitnesszbest;%记录群体极值,即目标函数最优解
end
s(g,:)=result;%重复100次试验+本身1次,所以最终k = 101
end
%% 绘图
%画出每代最优个体适应度值
for m=1:300
s(101,m)=sum( s(:,m) )/100;%将100次试验的个体适应度值放在最后一行
end
figure(1)
plot(s(101,:),'g','linewidth',1)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);
%画出整个迭代的寻优过程
figure(2)
plot(result,'r','linewidth',1)
title('寻优过程')
xlabel('进化代数','fontsize',12);ylabel('群体极值(最优解)','fontsize',12);
%画出目标函数三维图像
figure(3)
[x,y]=meshgrid(-2:0.01:2);
z=sin( sqrt(x.^2+y.^2) )./sqrt(x.^2+y.^2)+exp((cos(2*pi*x)+cos(2*pi*y))/2)-2.71289;
mesh(x,y,z)
hold on
plot(zbest,fitnesszbest,'*r')
运行结果:



注:
①先速度更新再位置更新
②有sizepop个粒子、maxgen次迭代,g次试验,所以嵌套关系维g > maxgen > sizepop
③为防止迭代寻优过程有位置或者速度越界/超出最大范围的情况,会进行越界处理
④由于目标函数峰谷较多,所以并非每次都能找到全局最优1.0054,有可能会找到局部最优0.8544、1.0053等,所以后面会改进权重因子。
2.2 线性递减惯性权重因子求解最大值问题
![]()



2.3 非线性递减惯性权重因子形①求解最大值问题

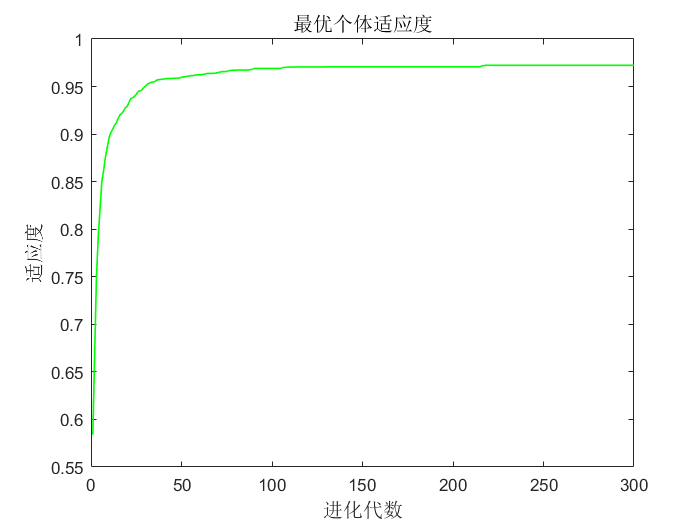

2.4 非线性递减惯性权重因子形②求解最大值问题



2.5 非线性递减惯性权重因子形③求解最大值问题

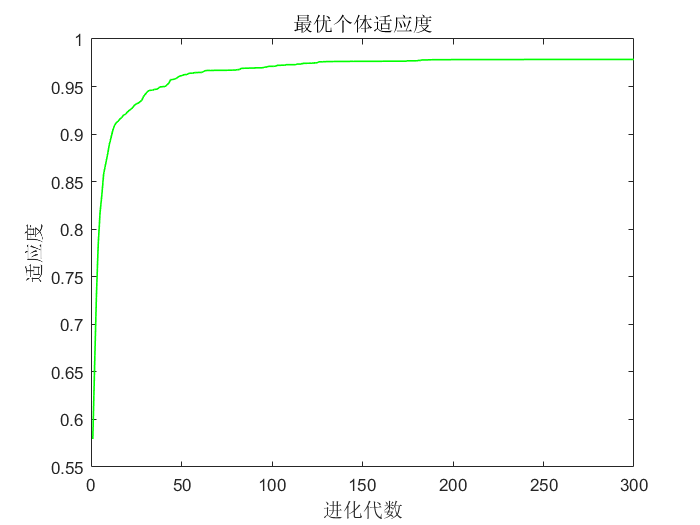

2.6 非线性递减惯性权重因子形④求解最大值问题


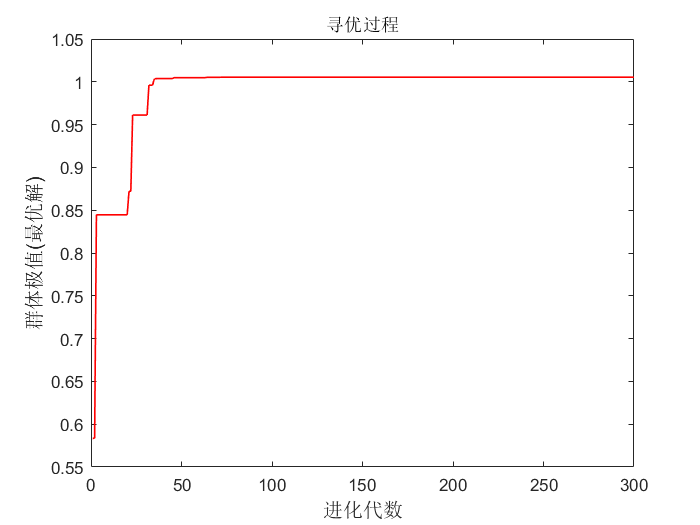
2.7 汇总对比
首先看一下ω惯性权重随迭代次数的动态变化:

再对比个体适应度值和目标函数寻优过程:


3. 粒子群算法求解最小值问题
如果是求解最小值,这个时候有两种方法:
①仍将适应度值定义为函数值,但此时无法正常求解适应度,但是可以正常得到寻优过程
将上述程序中这几行变动即可:
[bestfitness,bestindex] = min(fitness);
if fitness(j) < fitnessgbest(j)%仍将适应度值=目标函数值,即寻找最小的适应度
if fitness(j) < fitnesszbest%注:因为个体极值是一个数,所以不需要索引值
求解结果(常数惯性权重):

x=-1.5414,y=-1.5414时,最小值=-1.9562.
②将适应度函数取为目标函数的相反数,这样适应度越大,目标函数便越小,但是结果需要取反,因为目标函数那里取反了一次。
主程序主需将结果取反即可,即在记录群体极值前取反:
fitnesszbest = -fitnesszbest;
result(k) = fitnesszbest;%记录群体极值,即目标函数最优解

注:若使用常数惯性权重,并非每次都是找到全局最优。
4.总结
①可以看到常数惯性权重的粒子群算法虽然有较快的收敛速度,但是容易在后期陷入局部最优(因为后期适应度值很接近),导致求解精度低或者求解的是局部最优解;而几种动态的惯性权重虽然在迭代初期收敛较慢,但是后期局部搜索能力强,有利于跳出局部最优而求得最优解,提高了算法的求解精度。 所以ω和搜索能力的关系为,ω大全局寻优能力强,局部寻优能力弱。
②大家学习的时候一定要将去动态看程序,推荐使用断点调试去运行,结合工作区间去看变量变化,这样才能弄懂算法流程和感受算法的迭代。
注:本人也是在学习摸索的过程之中,如果有什么错误,欢迎指教,谢谢理解!
