当前位置：首页 > news >正文

二叉树9：二叉树的最大深度

news 来源：原创 2024/11/18 22:26:39

主要是我自己刷题的一些记录过程。如果有错可以指出哦，大家一起进步。
转载代码随想录
原文链接：
代码随想录
leetcode链接：
104. 二叉树的最大深度
559.n叉树的最大深度

104.二叉树的最大深度

题目：

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：

示例：
给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

思路：

看完本篇可以一起做了如下两道题目：

104.二叉树的最大深度
559.n叉树的最大深度

递归法

本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）
而根节点的高度就是二叉树的最大深度，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。

这一点其实是很多同学没有想清楚的，很多题解同样没有讲清楚。

我先用后序遍历（左右中）来计算树的高度。

确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。
代码如下：

int getdepth(treenode* node)

确定终止条件：如果为空节点的话，就返回0，表示高度为0。
代码如下：

if (node == NULL) return 0;

确定单层递归的逻辑：先求它的左子树的深度，再求右子树的深度，最后取左右深度最大的数值再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。
代码如下：

int leftdepth = getdepth(node->left);       // 左
int rightdepth = getdepth(node->right);     // 右
int depth = 1 + max(leftdepth, rightdepth); // 中
return depth;

所以整体c++代码如下：

class solution {
public:
    int getdepth(treenode* node) {
        if (node == NULL) return 0;
        int leftdepth = getdepth(node->left);       // 左
        int rightdepth = getdepth(node->right);     // 右
        int depth = 1 + max(leftdepth, rightdepth); // 中
        return depth;
    }
    int maxdepth(treenode* root) {
        return getdepth(root);
    }
};

代码精简之后c++代码如下：

class solution {
public:
    int maxdepth(treenode* root) {
        if (root == null) return 0;
        return 1 + max(maxdepth(root->left), maxdepth(root->right));
    }
};

精简之后的代码根本看不出是哪种遍历方式，也看不出递归三部曲的步骤，所以如果对二叉树的操作还不熟练，尽量不要直接照着精简代码来学。

本题当然也可以使用前序，代码如下：(充分表现出求深度回溯的过程)

class solution {
public:
    int result;
    void getdepth(treenode* node, int depth) {
        result = depth > result ? depth : result; // 中

        if (node->left == NULL && node->right == NULL) return ;

        if (node->left) { // 左
            depth++;    // 深度+1
            getdepth(node->left, depth);
            depth--;    // 回溯，深度-1
        }
        if (node->right) { // 右
            depth++;    // 深度+1
            getdepth(node->right, depth);
            depth--;    // 回溯，深度-1
        }
        return ;
    }
    int maxdepth(treenode* root) {
        result = 0;
        if (root == NULL) return result;
        getdepth(root, 1);
        return result;
    }
};

可以看出使用了前序（中左右）的遍历顺序，这才是真正求深度的逻辑！

注意以上代码是为了把细节体现出来，简化一下代码如下：

class solution {
public:
    int result;
    void getdepth(treenode* node, int depth) {
        result = depth > result ? depth : result; // 中
        if (node->left == NULL && node->right == NULL) return ;
        if (node->left) { // 左
            getdepth(node->left, depth + 1);
        }
        if (node->right) { // 右
            getdepth(node->right, depth + 1);
        }
        return ;
    }
    int maxdepth(treenode* root) {
        result = 0;
        if (root == 0) return result;
        getdepth(root, 1);
        return result;
    }
};

迭代法

使用迭代法的话，使用层序遍历是最为合适的**，因为最大的深度就是二叉树的层数**，和层序遍历的方式极其吻合。

在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，如图所示：
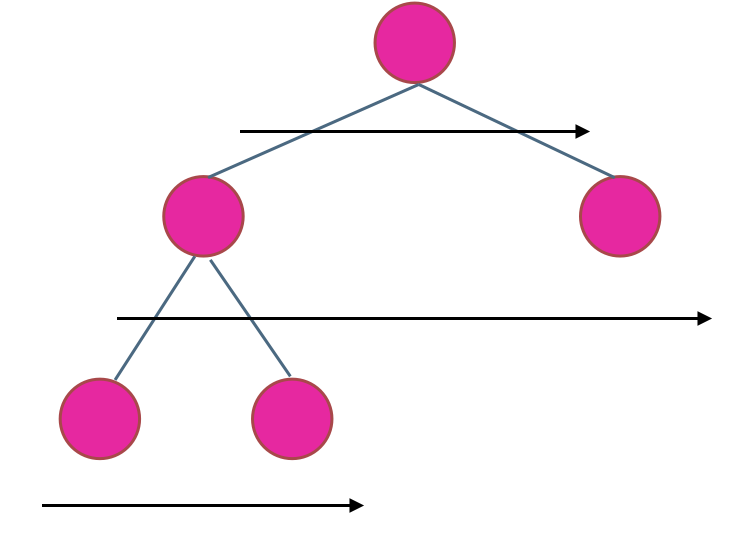
在这里插入图片描述
所以这道题的迭代法就是一道模板题，可以使用二叉树层序遍历的模板来解决的。
c++代码如下：

class solution {
public:
    int maxdepth(treenode* root) {
        if (root == NULL) return 0;
        int depth = 0;
        queue<treenode*> que;
        que.push(root);
        while(!que.empty()) {
            int size = que.size();
            depth++; // 记录深度
            for (int i = 0; i < size; i++) {
                treenode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return depth;
    }
};

那么我们可以顺便解决一下n叉树的最大深度问题

自己的代码

我自己这个其实是深度优先搜索的套路吧，只需要一个数值记录最大深度，然后用每一层的深度去和他做比较，保留最大深度就好了

class Solution {
public:
	void dfs(TreeNode* node, int depth, int& maxdepth) {
		if (!node) return;
		maxdepth = max(maxdepth, depth); //最大深度和当前深度比 取最大
		if(node->left)  dfs(node->left, depth+1, maxdepth);
		if (node->right) dfs(node->right, depth + 1, maxdepth);
	}

	int maxDepth(TreeNode* root) {
		if (!root) return 0;
		int depth = 1;
		int maxdepth = 1;
		dfs(root, depth, maxdepth);
		return maxdepth;
	}
};

559.n叉树的最大深度

题目

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

示例

示例 1：

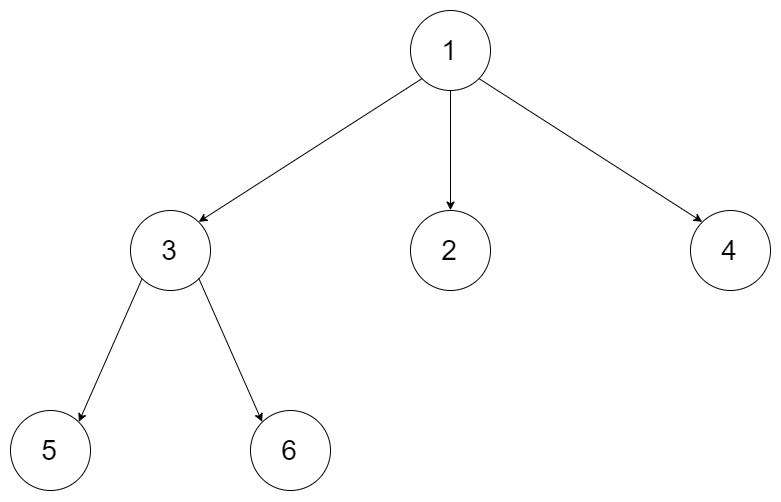
在这里插入图片描述

输入：root = [1,null,3,2,4,null,5,6]
输出：3

示例 2：

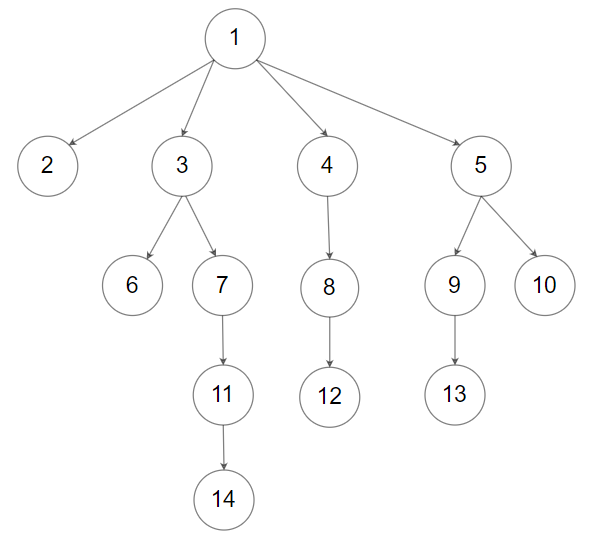
在这里插入图片描述

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：5

提示

树的深度不会超过 1000 。
树的节点数目位于 [0, 10⁴] 之间。

思路：

依然可以提供递归法和迭代法，来解决这个问题，思路是和二叉树思路一样的，直接给出代码如下：

递归法

c++代码：

class solution {
public:
    int maxdepth(node* root) {
        if (root == 0) return 0;
        int depth = 0;
        for (int i = 0; i < root->children.size(); i++) {
            depth = max (depth, maxdepth(root->children[i]));
        }
        return depth + 1;
    }
};

迭代法

依然是层序遍历，代码如下：

class solution {
public:
    int maxdepth(node* root) {
        queue<node*> que;
        if (root != NULL) que.push(root);
        int depth = 0;
        while (!que.empty()) {
            int size = que.size();
            depth++; // 记录深度
            for (int i = 0; i < size; i++) {
                node* node = que.front();
                que.pop();
                for (int j = 0; j < node->children.size(); j++) {
                    if (node->children[j]) que.push(node->children[j]);
                }
            }
        }
        return depth;
    }
};

自己的代码

思路和上面的递归法差不多，但是有一点点不一样吧。

class Solution {
public:
    int getMaxDepth(Node* node){
        if(!node) return 0;
        if(node->children.size()==0)return 1;
        int childrenMaxDepth=getMaxDepth(node->children[0]);
        for(int i=1;i<node->children.size();++i){
            childrenMaxDepth = max(childrenMaxDepth,getMaxDepth(node->children[i]));
        }
        return 1 + childrenMaxDepth;
    }

    int maxDepth(Node* root) {
        if(!root) return 0;
        return getMaxDepth(root);
    }
};