Cartesian product
In mathematics, specifically set theory, the Cartesian product of two sets A and B, denoted A × B, is the set of all ordered pairs (a, b) where a is in A and b is in B.[1] In terms of set-builder notation, that is
{\displaystyle A\times B={(a,b)\mid a\in A\ {\mbox{ and }}\ b\in B}.}{\displaystyle A\times B={(a,b)\mid a\in A\ {\mbox{ and }}\ b\in B}.}[2][3]
A table can be created by taking the Cartesian product of a set of rows and a set of columns. If the Cartesian product rows × columns is taken, the cells of the table contain ordered pairs of the form (row value, column value).[4]
One can similarly define the Cartesian product of n sets, also known as an n-fold Cartesian product, which can be represented by an n-dimensional array, where each element is an n-tuple. An ordered pair is a 2-tuple or couple. More generally still, one can define the Cartesian product of an indexed family of sets.
The Cartesian product is named after René Descartes,[5] whose formulation of analytic geometry gave rise to the concept, which is further generalized in terms of direct product.
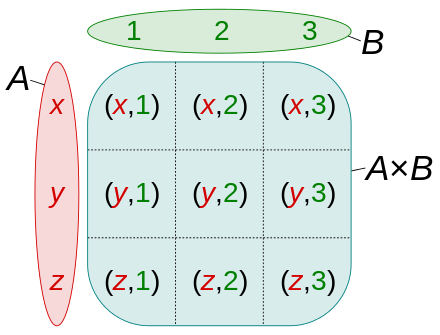
Cartesian product {\displaystyle \scriptstyle A\times B}\scriptstyle A\times B of the sets {\displaystyle \scriptstyle A={x,y,z}}\scriptstyle A={x,y,z} and {\displaystyle \scriptstyle B={1,2,3}}\scriptstyle B={1,2,3}
Contents
1 Examples
1.1 A deck of cards
1.2 A two-dimensional coordinate system
2 Most common implementation (set theory)
2.1 Non-commutativity and non-associativity
2.2 Intersections, unions, and subsets
2.3 Cardinality
3 Cartesian products of several sets
3.1 n-ary Cartesian product
3.2 n-ary Cartesian power
3.3 Infinite Cartesian products
4 Other forms
4.1 Abbreviated form
4.2 Cartesian product of functions
4.3 Cylinder
5 Definitions outside set theory
5.1 Category theory
5.2 Graph theory
6 See also
