三角函数公式
三角函数的定义
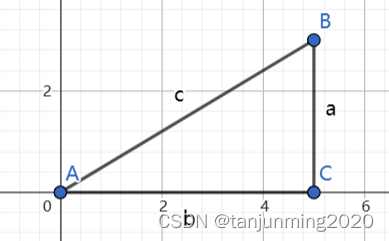
| 锐角三角函数 | 任意角三角函数 | |
|---|---|---|
| 正弦 | sin A = a c \sin A=\dfrac ac sinA=ca | sin θ = y r \sin \theta=\dfrac yr sinθ=ry |
| 余弦 | cos A = b c \cos A=\dfrac bc cosA=cb | cos θ = x r \cos \theta=\dfrac xr cosθ=rx |
| 正切 | tan A = a b \tan A=\dfrac ab tanA=ba | tan θ = y x \tan \theta=\dfrac yx tanθ=xy |
| 余切 | cot A = b a \cot A=\dfrac ba cotA=ab | cot θ = x y \cot \theta=\dfrac xy cotθ=yx |
| 正割 | sec A = c b \sec A=\dfrac cb secA=bc | sec θ = r x \sec \theta=\dfrac rx secθ=xr |
| 余割 | csc A = c a \csc A=\dfrac ca cscA=ac | csc θ = r y \csc \theta=\dfrac ry cscθ=yr |
函数的关系
- tan α cot α = 1 \tan \alpha\cot \alpha=1 tanαcotα=1
- sin α csc α = 1 \sin \alpha\csc \alpha=1 sinαcscα=1
- cos α sec α = 1 \cos \alpha\sec\alpha=1 cosαsecα=1
- tan α = sin α cos α \tan \alpha=\dfrac{\sin \alpha}{\cos \alpha} tanα=cosαsinα
- sin 2 α + cos 2 α = 1 \sin^2\alpha+\cos^2\alpha=1 sin2α+cos2α=1
三角函数公式
诱导公式
公式1
sin
(
2
k
π
+
α
)
=
sin
α
(
k
∈
Z
)
\sin(2k\pi+\alpha)=\sin \alpha \qquad (k\in Z)
sin(2kπ+α)=sinα(k∈Z)
cos
(
2
k
π
+
α
)
=
cos
α
(
k
∈
Z
)
\cos(2k\pi+\alpha)=\cos \alpha \qquad (k\in Z)
cos(2kπ+α)=cosα(k∈Z)
tan
(
2
k
π
+
α
)
=
tan
α
(
k
∈
Z
)
\tan(2k\pi+\alpha)=\tan \alpha \qquad (k\in Z)
tan(2kπ+α)=tanα(k∈Z)
cot
(
2
k
π
+
α
)
=
cot
α
(
k
∈
Z
)
\cot(2k\pi+\alpha)=\cot \alpha \qquad (k\in Z)
cot(2kπ+α)=cotα(k∈Z)
公式2
sin
(
π
+
α
)
=
−
sin
α
\sin(\pi+\alpha)=-\sin \alpha
sin(π+α)=−sinα
cos
(
π
+
α
)
=
−
cos
α
\cos(\pi+\alpha)=-\cos \alpha
cos(π+α)=−cosα
tan
(
π
+
α
)
=
tan
α
\tan(\pi+\alpha)=\tan \alpha
tan(π+α)=tanα
cot
(
π
+
α
)
=
cot
α
\cot(\pi+\alpha)=\cot \alpha
cot(π+α)=cotα
公式3
sin
(
−
α
)
=
−
sin
α
\sin(-\alpha)=-\sin \alpha
sin(−α)=−sinα
cos
(
−
α
)
=
cos
α
\cos(-\alpha)=\cos \alpha
cos(−α)=cosα
tan
(
−
α
)
=
−
tan
α
\tan(-\alpha)=-\tan \alpha
tan(−α)=−tanα
cot
(
−
α
)
=
−
cot
α
\cot(-\alpha)=-\cot \alpha
cot(−α)=−cotα
公式4
sin
(
π
−
α
)
=
sin
α
\sin(\pi-\alpha)=\sin \alpha
sin(π−α)=sinα
cos
(
π
−
α
)
=
−
cos
α
\cos(\pi-\alpha)=-\cos \alpha
cos(π−α)=−cosα
tan
(
π
−
α
)
=
−
tan
α
\tan(\pi-\alpha)=-\tan \alpha
tan(π−α)=−tanα
cot
(
π
−
α
)
=
−
cot
α
\cot(\pi-\alpha)=-\cot \alpha
cot(π−α)=−cotα
公式5
sin
(
2
π
−
α
)
=
−
sin
α
\sin(2\pi-\alpha)=-\sin \alpha
sin(2π−α)=−sinα
cos
(
2
π
−
α
)
=
cos
α
\cos(2\pi-\alpha)=\cos \alpha
cos(2π−α)=cosα
tan
(
2
π
−
α
)
=
−
tan
α
\tan(2\pi-\alpha)=-\tan \alpha
tan(2π−α)=−tanα
cot
(
2
π
−
α
)
=
−
cot
α
\cot(2\pi-\alpha)=-\cot \alpha
cot(2π−α)=−cotα
公式6
sin ( π 2 + α ) = cos α cos ( π 2 + α ) = − sin α tan ( π 2 + α ) = − cot α cot ( π 2 + α ) = − tan α \sin(\dfrac{\pi}{2}+\alpha)=\cos \alpha \quad \cos(\dfrac{\pi}{2}+\alpha)=-\sin \alpha \quad \tan(\dfrac{\pi}{2}+\alpha)=-\cot \alpha \quad \cot(\dfrac{\pi}{2}+\alpha)=-\tan \alpha sin(2π+α)=cosαcos(2π+α)=−sinαtan(2π+α)=−cotαcot(2π+α)=−tanα
sin ( π 2 − α ) = cos α cos ( π 2 − α ) = sin α tan ( π 2 − α ) = cot α cot ( π 2 − α ) = tan α \sin(\dfrac{\pi}{2}-\alpha)=\cos \alpha \quad \cos(\dfrac{\pi}{2}-\alpha)=\sin \alpha \quad \tan(\dfrac{\pi}{2}-\alpha)=\cot \alpha \quad \cot(\dfrac{\pi}{2}-\alpha)=\tan \alpha sin(2π−α)=cosαcos(2π−α)=sinαtan(2π−α)=cotαcot(2π−α)=tanα
sin ( 3 π 2 + α ) = − cos α cos ( 3 π 2 + α ) = sin α tan ( 3 π 2 + α ) = − cot α cot ( 3 π 2 + α ) = − tan α \sin(\dfrac{3\pi}{2}+\alpha)=-\cos \alpha \quad \cos(\dfrac{3\pi}{2}+\alpha)=\sin \alpha \quad \tan(\dfrac{3\pi}{2}+\alpha)=-\cot \alpha \quad \cot(\dfrac{3\pi}{2}+\alpha)=-\tan \alpha sin(23π+α)=−cosαcos(23π+α)=sinαtan(23π+α)=−cotαcot(23π+α)=−tanα
sin ( 3 π 2 − α ) = − cos α cos ( 3 π 2 − α ) = − sin α tan ( 3 π 2 − α ) = cot α cot ( 3 π 2 − α ) = tan α \sin(\dfrac{3\pi}{2}-\alpha)=-\cos \alpha \quad \cos(\dfrac{3\pi}{2}-\alpha)=-\sin \alpha \quad \tan(\dfrac{3\pi}{2}-\alpha)=\cot \alpha \quad \cot(\dfrac{3\pi}{2}-\alpha)=\tan \alpha sin(23π−α)=−cosαcos(23π−α)=−sinαtan(23π−α)=cotαcot(23π−α)=tanα
口诀:奇变偶不变,符号看象限。
\qquad
如果加的常数是
π
2
\dfrac{\pi}{2}
2π的奇数倍,则函数名称要变,正弦边余弦,余弦变正弦,正切变余切,余切变正切。是偶数倍则不变。
\qquad 因为 α \alpha α是任意角,在记公式的时候,我们不妨将 α \alpha α看作第一象限的角,那么此时 sin α , cos α tan α , cot α \sin \alpha,\cos \alpha\tan \alpha,\cot \alpha sinα,cosαtanα,cotα都为正。然后根据原函数的角度所在的象限来判断新函数的符号。
\qquad 举例:对于 sin ( 3 π 2 + α ) \sin(\dfrac{3\pi}{2}+\alpha) sin(23π+α),首先 3 π 2 \dfrac{3\pi}{2} 23π是 π 2 \dfrac{\pi}{2} 2π的三倍,所以要变函数名;又因为当 α \alpha α的终边在第一象限的时候 3 π 2 + α \dfrac{3\pi}{2}+\alpha 23π+α在第四象限,而正弦函数在第四象限值为负,所以 sin ( 3 π 2 + α ) = − cos α \sin(\dfrac{3\pi}{2}+\alpha)=-\cos \alpha sin(23π+α)=−cosα。
倍角公式
sin 2 α = 2 sin α cos α \sin 2\alpha=2\sin \alpha\cos \alpha sin2α=2sinαcosα
cos 2 α = cos 2 α − sin 2 α = 1 − 2 sin α = 2 cos 2 α − 1 \cos 2\alpha=\cos^2\alpha-\sin^2\alpha=1-2\sin \alpha=2\cos^2\alpha-1 cos2α=cos2α−sin2α=1−2sinα=2cos2α−1
tan 2 α = 2 tan α 1 − tan 2 α \tan 2\alpha=\dfrac{2\tan \alpha}{1-\tan^2\alpha} tan2α=1−tan2α2tanα
降幂公式
sin 2 α = 1 2 ( 1 − cos 2 α ) \sin^2\alpha=\dfrac 12(1-\cos2\alpha) sin2α=21(1−cos2α)
cos 2 α = 1 2 ( 1 + cos 2 α ) \cos^2\alpha=\dfrac 12(1+\cos2\alpha) cos2α=21(1+cos2α)
半角公式
sin α 2 = ± 1 − cos α 2 \sin\dfrac{\alpha}{2}=\pm\sqrt{\dfrac{1-\cos \alpha}{2}} sin2α=±21−cosα
cos α 2 = ± 1 + cos α 2 \cos\dfrac{\alpha}{2}=\pm\sqrt{\dfrac{1+\cos \alpha}{2}} cos2α=±21+cosα
tan α 2 = sin α 1 + cos α = 1 − cos α sin α = ± 1 − cos α 1 + cos α \tan\dfrac{\alpha}{2}=\dfrac{\sin \alpha}{1+\cos \alpha}=\dfrac{1-\cos \alpha}{\sin \alpha}=\pm\sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}} tan2α=1+cosαsinα=sinα1−cosα=±1+cosα1−cosα
正负由 α 2 \dfrac{\alpha}{2} 2α所在象限决定。因为带根号的数一定是非负数,所以可以根据原函数在对应象限的正负来判断新函数的正负。
和差公式
sin ( α ± β ) = sin α cos β ± cos α sin β \sin(\alpha\pm\beta)=\sin \alpha\cos \beta\pm\cos \alpha\sin \beta sin(α±β)=sinαcosβ±cosαsinβ
cos ( α ± β ) = cos α cos β ∓ sin α sin β \cos(\alpha\pm\beta)=\cos \alpha\cos \beta\mp\sin \alpha\sin \beta cos(α±β)=cosαcosβ∓sinαsinβ
tan ( α ± β ) = tan α ± tan β 1 ∓ tan α tan β \tan(\alpha\pm\beta)=\dfrac{\tan \alpha\pm\tan\beta}{1\mp\tan \alpha\tan \beta} tan(α±β)=1∓tanαtanβtanα±tanβ
积化和差公式
sin α cos β = 1 2 [ sin ( α + β ) + sin ( α + β ) ] \sin \alpha\cos \beta=\dfrac 12[\sin(\alpha+\beta)+\sin(\alpha+\beta)] sinαcosβ=21[sin(α+β)+sin(α+β)]
cos α sin β = 1 2 [ sin ( α + β ) − sin ( α − β ) ] \cos \alpha\sin \beta=\dfrac 12[\sin(\alpha+\beta)-\sin(\alpha-\beta)] cosαsinβ=21[sin(α+β)−sin(α−β)]
cos α cos β = 1 2 [ cos ( α + β ) + cos ( α − β ) ] \cos \alpha\cos \beta=\dfrac 12[\cos(\alpha+\beta)+\cos(\alpha-\beta)] cosαcosβ=21[cos(α+β)+cos(α−β)]
sin α sin β = 1 2 [ cos ( α − β ) − cos ( α + β ) ] \sin \alpha\sin \beta=\dfrac 12[\cos(\alpha-\beta)-\cos(\alpha+\beta)] sinαsinβ=21[cos(α−β)−cos(α+β)]
和差化积公式
sin α + sin β = 2 sin α + β 2 cos α − β 2 \sin \alpha+\sin \beta=2\sin\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2} sinα+sinβ=2sin2α+βcos2α−β
sin α − sin β = 2 cos α + β 2 sin α − β 2 \sin \alpha-\sin \beta=2\cos\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2} sinα−sinβ=2cos2α+βsin2α−β
cos α + cos β = 2 cos α + β 2 cos α − β 2 \cos \alpha+\cos \beta=2\cos\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2} cosα+cosβ=2cos2α+βcos2α−β
cos α − cos β = − 2 sin α + β 2 sin α − β 2 \cos \alpha-\cos \beta=-2\sin\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2} cosα−cosβ=−2sin2α+βsin2α−β
口诀
正加正,正在前;余加余,余并肩。
正减正,余在前;余减余,负正弦。
万能公式
sin α = 2 tan α 2 1 + tan 2 α 2 \sin \alpha=\dfrac{2\tan \frac{\alpha}{2}}{1+\tan^2\frac{\alpha}{2}} sinα=1+tan22α2tan2α
cos α = 1 − tan 2 α 2 1 + tan 2 α 2 \cos \alpha=\dfrac{1-\tan^2\frac{\alpha}{2}}{1+\tan^2 \frac{\alpha}{2}} cosα=1+tan22α1−tan22α
tan α = 2 tan α 2 1 − tan 2 α 2 \tan \alpha=\dfrac{2\tan\frac{\alpha}{2}}{1-\tan^2\frac{\alpha}{2}} tanα=1−tan22α2tan2α
