一.选择判断

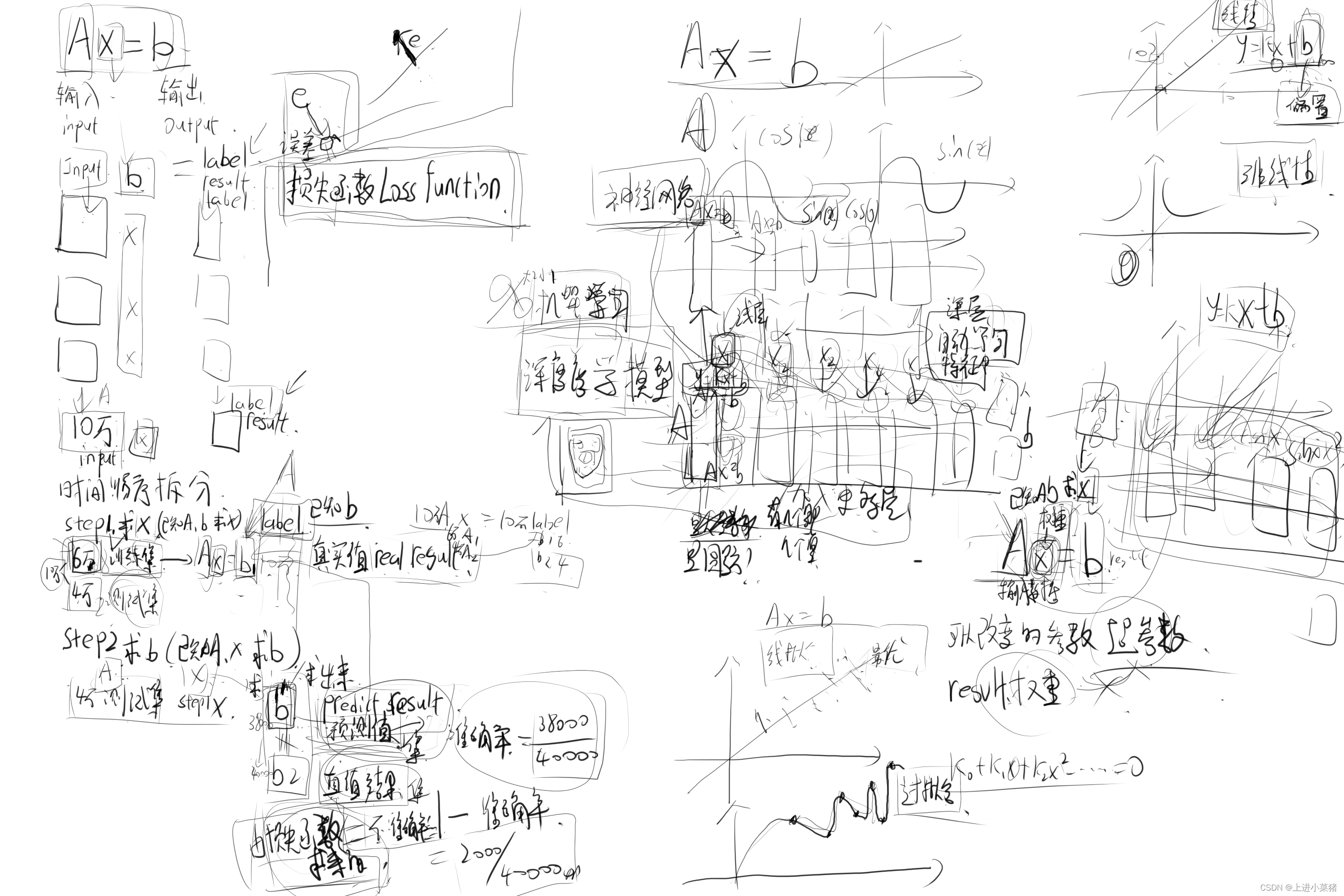
（输入值）input*b=lable（结果） 10万数据，进行拆分（时间、顺序）拆分。6w训练集 4万测试集

原：10w个input*b=10w个lable

step1：求x（已知A，b求X）AX=b1。这个b1为真实值（real result）

step2：求b（已知A，X求b） AX=b2。这个b2为预测结果（predict result）

假如在4万测试集里，有4W个结果

• b2(预测)不等于b(真实值结果)

• 准确率=38000/40000

• 损失函数=1-准确率 损失函数越大，准确率越低。

• 损失函数和预测值和真实结果有关。和训练集、测试集无关。

1.1矩阵与 神经网络模型 与 深度学习模型 关系

神经网络：一层：简单神经网络 多层：深度学习模型（加入了更多的层）

• 每一层解决不同的问题。

• 自动学习特征。

题目要点：

• 矩阵，输入的矩阵数据。

• 多个经网络模型就是深度学习模型

1.2 机器学习 与 深度学习 在训练数据中的区别

题目要点：

机器学习自己找特征，深度学习可以自己找特征。

1.3点乘与叉乘区别

点乘是两个向量的数量积，点乘后为一个数，而叉乘的结果为一个向量。

点乘，也叫数量积。结果是一个向量在另一个向量方向上投影的长度，是一个标量。

叉乘，也叫向量积。结果是一个和已有两个向量都垂直的向量。

1.4 深度学习模型 浅层与深层 关系

浅层与深层在神经网络中：

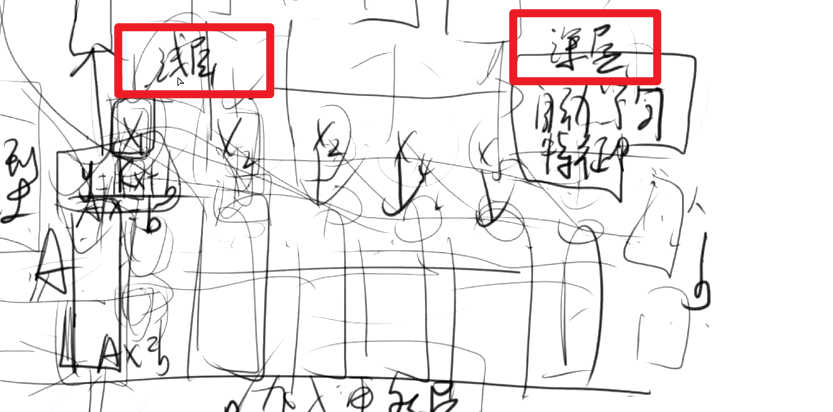
深层比浅层可以解决更多复杂的问题。

题目要点：

• 浅层指简单问题。
• 深层指更复杂的问题。

1.5线性关系与非线性 权重和偏置

• 线性关系与非线性：

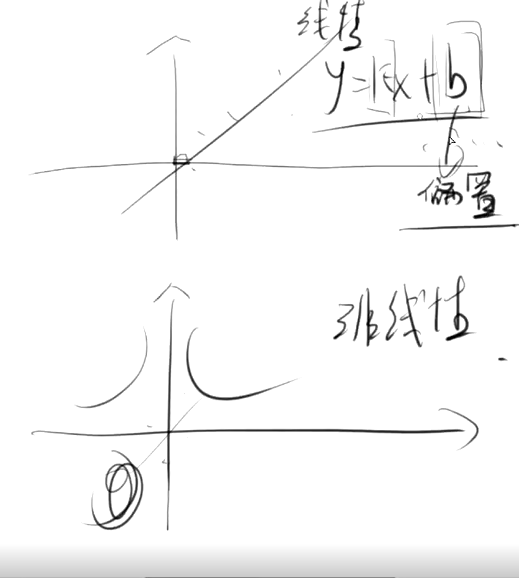
题目要点：

• y=kx+b ：b就是偏置。

• 线性关系里用到了偏置。

1.6 超参数（训练数据与可调整数据（var））

A(输入数据)x(权重)=b 已知Ab求X。

A和b可以改变，x不能改变

• 训练当中可以改变的量：超参数

• result权重不是超参数

• 训练数据不属于超参数

• 可调整数据不一定是超参数（因为里面还包含训练数据）

• 超参数一定是可调整数据

1,7 误差其他说法 损失函数Loss fuction 预测值与真实值之间的差距

• 预测值：通过一部分的训练集得到x，然后在训练集里已知A，x求b ，b就是预测值
• 真实值：给的结果。
• 损失函数：不准确率和损失函数有关。
• 损失函数=1-准确率 损失函数越大，准确率越低。

1.8 线性，非线性与过拟合

线性关系不能拟合全部的点：最优。有误差

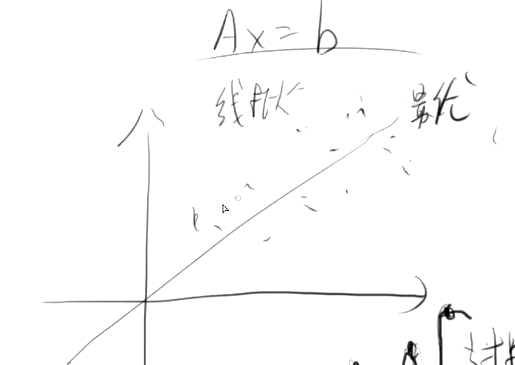
非线性完全拟合全部的点

非线性才有过拟合。

二.大题

数据去粗取精，求最优

稀疏矩阵特点以及应用

2.1作业一： 开放性的问题 1.数据选择的问题，选择什么样的数据进行分析？如果出现数据与当前分析内容预测不一致，该如何解决？

有目的的收集数据，是确保数据分析过程有效的基础。组织需要对收集数据的内容、渠道、方法进行策划。策划时应考虑
①将识别的需求转化为具体的要求，如评价供方时，需要收集的数据可能包括其过程能力、测量系统不确定度等相关数据
②明确由谁在何时何处，通过何种渠道和方法收集数据
③记录表应便于使用；
④采取有效措施，防止数据丢失和虚假数据对系统的干扰。
2.如果出现数据与当前分析内容预测不一致，该如何解决？
当数据出现不一致性时，需要对数据进行清洗和集成操作，去除冗余数据、统一变量名、统一数据的计量单位等，并使用最新的数据来消除不一致性。
第一，查看原始数据中都会存在不完整，不一致、数据异常等问题，这类数据会降低数据的质量，影响数据分析的结果。第二，数据的缺失一般是指观测的缺失和观测中变量值的缺失，两者都会造成分析结果的不准确。可以忽略确实值的误差

2.2作业二补充（选做的）：稀疏矩阵问题 ，我们在学习的过成功什么地方提到了稀疏矩阵，稀疏矩阵的特点是什么。

稀疏矩阵算法的最大特点是通过只存储和处理非零元素从而大幅度降低存储空间需求以及计算复杂度，代价则是必须使用专门的稀疏矩阵压缩存储数据结构。

对于矩阵而言，稀疏矩阵，就是大部分数据都为0，少部分不为0，稀疏正是指”非0数据很少。
对于大型矩阵，例如矩阵维度超过10000，那么稀疏矩阵不仅节省存储空间，并且可以让线性代数算法得到极大的加速。

2.3作业四 ： Ax=0 与 Ax=b 他们之间的关系。 文字进行叙述 。

1.Ax=0有解不一定Ax=b有解
2.Ax=b的任意两个不相同的解得差就是Ax=0的一个非零解。
3.Ax=b有解的话，Ax=0必有解
4.Ax=b的通解是Ax=0的解

Ax=0与Ax=b的解的关系：
1、AX=0有解不一定AX=b有解，即是AX=B有解是AX=0有解的充分非必要条件。
2、假设b1和b2都是Ax=b的解，那么有Ab1=b，Ab2=b，将两式相减，Ab1-Ab2=b-b，即A(b1-b2)=0，则b1-b2是齐次方程Ax=0的解。即AX=b的任意两个不相同的解得差就是AX=0的一个非零解。
Ax=0通解的表示：设R(A)=R(B)=r；把行最简形中r个非零行的非0首元所对应的未知数用其余n-r个未知数（自由未知数）表示，即可写出含n-r个参数的通解。
Ax=b的通解=Ax=b的通解=Ax=0的通解+Ax=b的一个特解（η=ζ+η*）。
扩展资料：
非齐次线性方程组Ax=b有解的充分必要条件是：系数矩阵的秩等于增广矩阵的秩，即rank(A)=rank(A, b)（否则为无解）。
非齐次线性方程组有唯一解的充要条件是rank(A)=n。
非齐次线性方程组有无穷多解的充要条件是rank(A)<n。（rank(A)表示A的秩）

AX=0是AX=B的齐次线性方程
两个解得关系
AX=0有解不一定AX=B有解，反之则成立。即是AX=B有解是AX=0有解的充分非必要条件。
假设X1，X2是AX=B的两个不相同的解，则X1-X2是AX=0的一个非零解，即AX=B的任意两个不相同的解得差就是AX=0的一个非零解
通解表示
若AX=B有解，假设Y是AX=B一个特解
先解AX=0，得出其基础解系为X1，X2，X3，X4。。。。XN
折AX=B的通解就可以表示成X=K1X1+K2X2+K3X3+。。。。+KNXN+Y
其中K1,K2,K3,.......KN是任意常数

2.4作业四补充（选做的） Ax=0 与 Ax=b 他们之间的关系 补充加入 零空间 列空间 y的转置乘以A 行空间之间的关系。 可以用写下来 用文字也可以用公式推导，也可以二者结合