【矩阵论】7. 范数理论——非负/正矩阵

7.5 非负/正矩阵

7.5.1 定义

a. 非负/正矩阵定义

一个实矩阵 $A=(a_{ij})\in R^{m\times n}$

• 若对每一 $i$ 和 $j$ ，$a_{ij}\ge 0$ ，则称A是非负矩阵，$A\ge 0$

• 若对每一 $i$ 和 $j$ ，$a_{ij}>0$ ，则称A是正矩阵，$A>0$

b. 矩阵大小关系

设 $A,B\in C^{n\times n}$

• 如果 $A-B\ge 0$ ，则写 $A\ge B$
• 如果 $A-B>0$ ,则 $A>B$

c. 绝对矩阵

设 $A=(a_{ij}{)}_{m\times n}$ ，规定其绝对矩阵为 $|A|\stackrel{\Delta }{=}(|a_{ij}|)$

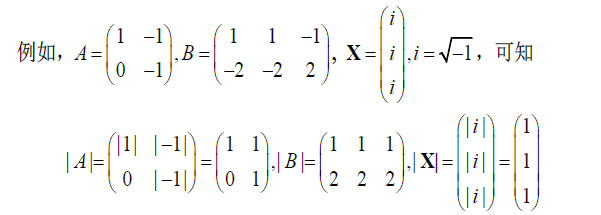
7.5.2 性质

设 $A=(a_{ij}{)}_{m\times n}，B=(b_{ij}{)}_{m\times n}$ ，有

1. $|A|=(|a_{ij}|)\ge 0$ ；$|A|=0$ 当且仅当 $A=0$

2. $|kA|=|k|\cdot |A|,k\in C$

3. $|A^k|\le |A{|}^k,k=1,2,\cdots$

4. 若 $A>0$ ，则 $A^k>0，k=1,2,\cdots$

5. $|A+B|\le |A|+|B|$

6. 如果 $A\ge 0，A\ne 0$ ，则 $A>0$ 不一定成立

   $\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\ge 0$ ，但 $A$ 不是正矩阵

7. 若 $A\ge 0,B\ge 0,a\ge 0,b\ge 0$ ，则 $aA+bB\ge 0$

8. $A\ge B,C\ge D$，则 $A+C\ge B+D$

9. $A\ge B,B\ge C$ ，则 $A\ge C$

设 $A，B，C，D\in C^{n\times n}$ ，$x,y\in C^n$

1. $|Ax|\le |A|\cdot |x|$

2. 若 $0\le A\le B,0\le C\le D$ ，则 $0\le AC\le AD \le BD $

3. 若 $0\le A\le B$ ，则 $0\le A^k\le B^k,k=1,2,\cdots$

4. 若 $|A|\le |B|$ ，则范数 $\Vert A{\Vert }_F\le \Vert B{\Vert }_F$ ，且 $\Vert A{\Vert }_1\le \Vert B{\Vert }_1$

5. $非负向量\times 正矩阵\Rightarrow 正向量$ ：若 $A>0$，且 $ x\ge 0$ ，则 $Ax>0$

   $正向量\times 非负矩阵(不存在0行)\Rightarrow 正向量$ ：若 $A\ge 0,x>0$ ,且 $A的各行不是0$ ，则也有 $Ax>0$

   $正向量\times 非负矩阵=\vec{0}\Rightarrow A是0阵$ ：若 $A\ge 0,x>0$ 且 $Ax=0$ ，则 $A=0$

   若 $A\ge B,x>0$ ，且 $Ax=Bx$ ，则 $A=B$

7.5.3 正矩阵与谱半径定理

a. 范数约束谱半径

设非负阵 $A=(a_{ij}{)}_{n\times n}\ge 0$ ，

• 令 $h=A的最小行和$ ,$l=A的最小列和$

  $h\le \rho (A)\le \Vert A{\Vert }_{\infty }$

  $l\le \rho (A)\le \Vert A{\Vert }_1$

• $A$ 的各行(或列)的和为正，则 $\rho (A)>0$

• A没有0行（或0列），则可知 $\rho (A)>0$

设正矩阵 $A=(a_{ij}{)}_{n\times n}>0$ ，令 $h=A的最小行和$ ,$l=A的最小列和$

• $h<\rho (A)<\Vert A{\Vert }_{\infty }$
• $l<\rho (A)<\Vert A{\Vert }_1$
• $\rho (A)>0$

eg

$$\begin{array}{rl}& B为正矩阵，h=\frac{4}{5},\Vert B{\Vert }_{\infty }=1,l=\frac{47}{60},\Vert B{\Vert }_1=\frac{62}{60}\\ & \frac{4}{5}<\rho (B)<1,\frac{47}{60}<\rho (B)<\frac{62}{60}\end{array}$$

b. 矩阵间谱半径关系

设 $A,B\in C^{n\times n}$ ，$|A|\le B$ ，则 $\rho (A)\le \rho (|A|)<\rho (B)$

$0\le A\le B$ ，则 $\rho (A)\le \rho (B)$

$A\ge 0$ ，D为A中任一主子阵，则 $\rho (A)\ge \rho (D)$

$A>0$ ，则 $\rho (A)>0$

$0\le A<B$ ，则 $\rho (A)<\rho (B)$ ，

设 $A\ge 0$

• 若 $A$ 的每个行和为常数 $a$ ，则 $\rho (A)=a=\Vert A{\Vert }_{\infty }$

• 若 $A$ 的每个列和为常数 $b$ ，则 $\rho (A)=b=\Vert A{\Vert }_1$

c. 谱半径与特向特根关系

引理：

设 $A=(a_{ij}{)}_{n\times n}\ge 0$ ，任取正向量 $X=\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right)>0$ ，则

• $\underset{i}{\min }\left(\frac{1}{x_i}\sum _{j=1}^n{a}_{ij}{x}_j\right)\le \rho (A)\le \underset{i}{\max }\left(\frac{1}{x_i}\sum _{j=1}^n{a}_{ij}{x}_j\right)$

  $\rho (A)$ 的范围与乘积元素的最小值和最大值有关

  $\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{i1}& a_{i2}& \cdots & a_{in}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right)\left(\begin{array}{c}{x}_1\\ ⋮\\ x_i\\ ⋮\\ x_n\end{array}\right)=\left(\begin{array}{c}\sum _{j=1}^n(a_{1j}{x}_j)\\ ⋮\\ \sum _{j=1}^n(a_{ij}{x}_j)\\ ⋮\\ \sum _{j=1}^n(a_{nj}{x}_j)\end{array}\right)$

设 $A=(a_{ij}{)}_{n\times n}\ge 0$ ，$AX={\lambda }_{1}X$ ，$X=\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right)>0(正向量)$ 则有 $\rho (A)={\lambda }_1$

证明：
$$\begin{array}{rl}& 若AX={\lambda }_{1}X,则\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{i1}& a_{i2}& \cdots & a_{in}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right)\left(\begin{array}{c}{x}_1\\ ⋮\\ x_i\\ ⋮\\ x_n\end{array}\right)=\left(\begin{array}{c}\sum _{j=1}^n(a_{1j}{x}_j)\\ ⋮\\ \sum _{j=1}^n(a_{ij}{x}_j)\\ ⋮\\ \sum _{j=1}^n(a_{nj}{x}_j)\end{array}\right)\\ & \therefore \sum _{j=1}^n(a_{ij}{x}_j)={\lambda }_1{x}_i\Rightarrow {\lambda }_1=\frac{1}{x_i}\sum _{j=1}^n(a_{ij}{x}_j)\\ & 由引理，{\lambda }_1=\underset{i}{\min }\left(\frac{1}{x_i}\sum _{j=1}^n{a}_{ij}{x}_j\right)\le \rho (A)\le \underset{i}{\max }\left(\frac{1}{x_i}\sum _{j=1}^n{a}_{ij}{x}_j\right)={\lambda }_1\\ & \therefore {\lambda }_1恰为谱半径\rho (A)\end{array}$$

推论

设 $x=\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right)>0$ ，$A=(a_{ij}{)}_{n\times n}\ge 0$ ， $a\ge 0,b\ge 0$

• 若 $aX\le Ax\le bX$ ，则 $a\le \rho (A)\le b$
• 若 $aX<Ax<bX$ ，则 $a<\rho (A)<b$

若 $X\ge 0$ ，$A>0$

• 若 $AX=\lambda X$ ，则 $A$ 有正特征向量 $X>0$ ，且 $\lambda =\rho (A)$

配龙定理

设 $A=A_{n\times n}>0$

• $\rho (A)>0$ 且 $\rho (A)$ 恰是 $A$ 的正特根
• 存在正特根 $x>0$ ，使 $Ax=\rho (A)x$
• $\rho (A)$ 是 $A$ 的单特根
• 若特根 $\lambda \ne \rho (A)$ ，则 $|\lambda |<\rho (A)$ （$\rho (A)$为唯一极大模特征根）