NewStarCTF公开赛week3密码学前两道题的wp
目录
- 一、keyExchange
- 1.原题
- 2.考察知识点与解题思路
- Diffie-Hellman密钥交换
- 3.解题脚本
- 二、Prof. Shamir's Secret
- 1.原题
- 2.考察知识点与解题思路
- Shamir 门限方案
- 3.解题脚本
一、keyExchange
1.原题
题目给出的是题目给出的是加密过程和输出:
from secret import flag, gb, g, p, Diffie_Hellman_KEY_EXCHANGE
from Crypto.Util.number import *
from base64 import b64encode
from Crypto.Cipher import AES
from hashlib import md5
from Crypto.Util.Padding import pad
plaintext = pad(flag, 16)
a = getRandomNBitInteger(1024)
shared = Diffie_Hellman_KEY_EXCHANGE(a) # the original one, not the elliptic curve version!!!!
key = md5(str(shared).encode()).digest()
cipher = AES.new(key, AES.MODE_ECB)
ciphertext = cipher.encrypt(plaintext)
print(f'师傅给你送了一个flag')
print(f'加密的flag = {b64encode(ciphertext)}')
print(f'p = {p}')
print(f'your secret key {a}')
print(f'g = {g}')
print(f'师傅的公钥 = {gb}')
可以从加密过程的说明脚本中看出,输出的信息有:经过AES加密后又base64编码的flag(所以解AES前要先解码base64呀)、p、g、我方私钥a和师傅的公钥gb:
师傅给你送了一个flag
加密的flag = b'w8OCrexPPqnv2hR+xKeHhXIp0Blp1DYCV4LeZeeLpv5MzUL71raTOeOs4SQBySHH'
p = 133448764119399847876731592238604881175769007976799828874328988761588128500145459082023001027383524831194316266946485380737147372837136403065060245135035225976604193830121124575947440188318348815263642243784574567832213775382081426762862856428888257126982268557543952549848053225651398101391048467656128070913
your secret key 141940531741414073502483547551457269459744373002985569536254444581939073930343975447649087549033350166772929396986965301002444997704537487577508504709368627174241095027876996113941220579274986994026832534664179333669861059196192190040046004398523932288881838011696679341328520530265002776147308306715042734185
g = 3
师傅的公钥 = 89434791765835058026108803508194156525355359465406829253856379139334424137549915669535243140614128105195584073112084994777148895681804127886440617684648237403345873311011154293855911891719204975035914932661810961867593769891076834656437254428353814290948181922438812745384577094827728409350756648446941874382
2.考察知识点与解题思路
Diffie-Hellman密钥交换
具体的理论知识可参考博客:http://t.csdn.cn/fjnn8
Diffie-Hellman算法可以使两个用户之间安全地交换一个密钥,但不能用于加密或解密信息。(但这里感觉也不能说“安全”因为无法抵御中间人攻击?
为了方便思路与代码对照,我还是说一下理论知识和思路。
在题目中都是已知的g和p,分别是算法中的底数g和模数p。
设有两个要交换密钥(公钥)的用户A和用户B
用户A的私钥是a,计算g^a mod p = AKey,AKey是用户A要发送给用户B的公钥
用户B的私钥是b,计算g^b mod p = BKey,BKey是用户B要发送给用户A的公钥
用户A拿到B发来的BKey后,计算BKey^a mod p=key,用户B拿到用户A发来的AKey后,计算AKey^b mod p=key,这二者的值应该是相同的key,也就是两人协商出的密钥。
现在根据题目已经已知了我方私钥a、对方公钥BKey、模数p,已经可以直接计算BKey^a mod p得到双方协商出的密钥key(脚本中命名为shared)。
然后根据题目脚本中key = md5(str(shared).encode()).digest(),要将shared转str、encode后再做md5得到AES加密用的密钥key,就原样复制这条语句到解密脚本中即可。
再根据之前对题目脚本中输出内容的分析,对密文形式的flag先做base64解码。
最后用密钥key解密AES得到明文flag。
3.解题脚本
import base64
import hashlib
from Crypto.Cipher import AES
a=141940531741414073502483547551457269459744373002985569536254444581939073930343975447649087549033350166772929396986965301002444997704537487577508504709368627174241095027876996113941220579274986994026832534664179333669861059196192190040046004398523932288881838011696679341328520530265002776147308306715042734185
p=133448764119399847876731592238604881175769007976799828874328988761588128500145459082023001027383524831194316266946485380737147372837136403065060245135035225976604193830121124575947440188318348815263642243784574567832213775382081426762862856428888257126982268557543952549848053225651398101391048467656128070913
BKey=89434791765835058026108803508194156525355359465406829253856379139334424137549915669535243140614128105195584073112084994777148895681804127886440617684648237403345873311011154293855911891719204975035914932661810961867593769891076834656437254428353814290948181922438812745384577094827728409350756648446941874382
shared=pow(BKey,a,p)
key = hashlib.md5(str(shared).encode()).digest() #key=b'\xaep\x1f\xb5\x04\x9b.\x94\xd2:C\x1a\xd4<,\xce'
flag=b'w8OCrexPPqnv2hR+xKeHhXIp0Blp1DYCV4LeZeeLpv5MzUL71raTOeOs4SQBySHH'
flag=base64.b64decode(flag) #先解码base64
cipher = AES.new(key, AES.MODE_ECB)
flag=cipher.decrypt(flag) #对base64解码后的密文做AES解密
print(flag)
flag: flag{d1ff1e_h311m4n_is_4_p13c3_0f_c4k3}
二、Prof. Shamir’s Secret
1.原题
题目给出的是加密过程和输出:
from Crypto.Util.number import *
from secret import flag
a = getPrime(256)
b = getPrime(256)
c = getPrime(256)
d = bytes_to_long(flag)
n = getStrongPrime(2048)
def poly(x):
return (a * x ** 3 + b * x ** 2 + c * x + d) % n
for _ in range(4):
x = getRandomNBitInteger(256)
print(f'({x}, {poly(x)})')
print(n)
从脚本可以看出,输出的是循环中的4个(x值, 当前x对应的poly(x)的计算值)和n:
(107156592202708719207677242145785380370925248573491581679548864240229105117413, 130345771647598884054430192964980389494531690916321281560051538057910945565624075918097771618618910263287152864051564635195578796179646674192491555857366963976329072793625649841007238934532144994966695961491116944111900519450656607199501654544809304677384301432194356761274376314501143216649135187625964931902)
(90629424458637844580841178302065768114471702341586161908858665404968070428143, 78858394764644720845979385422903377630845158220853604360871859882044655577246282808874532941560824773914594412415345616068416548364923695233972936176087206729847544516343237888024173952758718279163069742944961359652574962129434781851767007643037433981750489254639449637677610354746497770492254725894119193662)
(100626477579781167218124067468465940736522526684796828200460725563611057086831, 107938673826832098883774065383352754899611421173786919174851524067358319831595518533880365335333592351382030254987030861475878447430100862628809476494215295084769705787398168068863060859122952000010558086859754975554734850230223040925027217057055876423229204027280075168615462165634569977166298865366648414270)
(93935717805931479760310332373603550626215862380271563609987050092246456803681, 87807687834883656794449107852803757931909462710953942209358337840912886376275257864214018767300085688088981183791568376874906785193974861264511995029891797395218085734556515485224508250678274640400740193260888803386269425525930551167801371074041851406813322268615707951973495879968706624649318162995708734670)
31332583438236375592937719796184754941510418106758544436807128579095975774977164550965999210436423180868482749439792419270701760326867558983833590368116755394302102816558834270767750410927007254951332459412016857259923960095221831744199277859298274645778838122123090174549834537459028702418645316659860963695912411044490603690484176741018002722235584411422885336520840416125528921196994346534698226763483608314982898155320734426983215291745003213365884087604024203316024824786079501166114638727651689476288442288919373885358425210859822108037791909364199015379638899887715692181883916583183449343868694265742569597579
2.考察知识点与解题思路
Shamir 门限方案
关于Shamir门限的理论知识可以参考博客:http://t.csdn.cn/wvS1Z
我就是从这里学到的O(∩_∩)O
放到这题大概就是:
1)有秘密藏在了多项式里,想恢复出秘密需要“多项式的次数+1”个子密钥,这里的“多项式次数+1”就是“门限”,子密钥即多项式的计算值f(x),这里是三次多项式,又已知了4个x和4个多项式的计算结果,模数n也已知,所以可以解题。
2)将已知条件代入,利用公式计算出结果转成bytes输出即是flag。
解密公式:
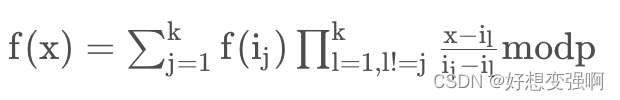
ps:公式中的p,在题目中对应的是n,f(i)即poly(x)的值
对应到题目,有k=4,在累加项中,j取1~4,f(i)取f(x1)~f(x4),f(i)后面累乘项的分子是用x(这里x就是字母x本身!)分别减去除当前的x值(注意是“值”,指x1/x2/x3/x4中的某一个)之外的3个x值,分母是用当前x值减去除当前的x值(指x1/x2/x3/x4中的某一个)之外的3个x值。将4组运算结果累加,得到的多项式中的字母x取0(即只保留常数项),最后再去模大数n。
3.解题脚本
在我的脚本中,x1~x4表示已知的4个x,rm1~rm4代表的是x对应的poly(x)的计算值,因为分子上有三个(x-i)项相乘所以得到的常数项符号位负,所以要在最前面手动添一个负号,对于分母的计算,是对模数n求乘法逆元。
import gmpy2
import libnum
x1=107156592202708719207677242145785380370925248573491581679548864240229105117413
rm1=130345771647598884054430192964980389494531690916321281560051538057910945565624075918097771618618910263287152864051564635195578796179646674192491555857366963976329072793625649841007238934532144994966695961491116944111900519450656607199501654544809304677384301432194356761274376314501143216649135187625964931902
x2=90629424458637844580841178302065768114471702341586161908858665404968070428143
rm2=78858394764644720845979385422903377630845158220853604360871859882044655577246282808874532941560824773914594412415345616068416548364923695233972936176087206729847544516343237888024173952758718279163069742944961359652574962129434781851767007643037433981750489254639449637677610354746497770492254725894119193662
x3=100626477579781167218124067468465940736522526684796828200460725563611057086831
rm3=107938673826832098883774065383352754899611421173786919174851524067358319831595518533880365335333592351382030254987030861475878447430100862628809476494215295084769705787398168068863060859122952000010558086859754975554734850230223040925027217057055876423229204027280075168615462165634569977166298865366648414270
x4=93935717805931479760310332373603550626215862380271563609987050092246456803681
rm4=87807687834883656794449107852803757931909462710953942209358337840912886376275257864214018767300085688088981183791568376874906785193974861264511995029891797395218085734556515485224508250678274640400740193260888803386269425525930551167801371074041851406813322268615707951973495879968706624649318162995708734670
n=31332583438236375592937719796184754941510418106758544436807128579095975774977164550965999210436423180868482749439792419270701760326867558983833590368116755394302102816558834270767750410927007254951332459412016857259923960095221831744199277859298274645778838122123090174549834537459028702418645316659860963695912411044490603690484176741018002722235584411422885336520840416125528921196994346534698226763483608314982898155320734426983215291745003213365884087604024203316024824786079501166114638727651689476288442288919373885358425210859822108037791909364199015379638899887715692181883916583183449343868694265742569597579
m1=-rm1*x2*x3*x4*gmpy2.invert((x1-x2)*(x1-x3)*(x1-x4),n)
m2=-rm2*x1*x3*x4*gmpy2.invert((x2-x1)*(x2-x3)*(x2-x4),n)
m3=-rm3*x1*x2*x4*gmpy2.invert((x3-x1)*(x3-x2)*(x3-x4),n)
m4=-rm4*x1*x2*x3*gmpy2.invert((x4-x1)*(x4-x2)*(x4-x3),n)
m=(m1+m2+m3+m4)%n
print(libnum.n2s(int(m)))
运行脚本可以直接得到flag。
flag: flag{w0w_y0u_k0nw_sham1r_s3cret_5h4r1ng_4nd_1agrange_interpolation!!!}
在别人的博客上看到的另一种解法但没看懂,先记录一下:参考来源
import gmpy2
import libnum
x1=107156592202708719207677242145785380370925248573491581679548864240229105117413
rm1=130345771647598884054430192964980389494531690916321281560051538057910945565624075918097771618618910263287152864051564635195578796179646674192491555857366963976329072793625649841007238934532144994966695961491116944111900519450656607199501654544809304677384301432194356761274376314501143216649135187625964931902
x2=90629424458637844580841178302065768114471702341586161908858665404968070428143
rm2=78858394764644720845979385422903377630845158220853604360871859882044655577246282808874532941560824773914594412415345616068416548364923695233972936176087206729847544516343237888024173952758718279163069742944961359652574962129434781851767007643037433981750489254639449637677610354746497770492254725894119193662
x3=100626477579781167218124067468465940736522526684796828200460725563611057086831
rm3=107938673826832098883774065383352754899611421173786919174851524067358319831595518533880365335333592351382030254987030861475878447430100862628809476494215295084769705787398168068863060859122952000010558086859754975554734850230223040925027217057055876423229204027280075168615462165634569977166298865366648414270
x4=93935717805931479760310332373603550626215862380271563609987050092246456803681
rm4=87807687834883656794449107852803757931909462710953942209358337840912886376275257864214018767300085688088981183791568376874906785193974861264511995029891797395218085734556515485224508250678274640400740193260888803386269425525930551167801371074041851406813322268615707951973495879968706624649318162995708734670
n=31332583438236375592937719796184754941510418106758544436807128579095975774977164550965999210436423180868482749439792419270701760326867558983833590368116755394302102816558834270767750410927007254951332459412016857259923960095221831744199277859298274645778838122123090174549834537459028702418645316659860963695912411044490603690484176741018002722235584411422885336520840416125528921196994346534698226763483608314982898155320734426983215291745003213365884087604024203316024824786079501166114638727651689476288442288919373885358425210859822108037791909364199015379638899887715692181883916583183449343868694265742569597579
def GCRT(x,rm):
curx,currm=x[0],rm[0]
for (xi,rmi) in zip(x[1:],rm[1:]):
d=gmpy2.gcd(curx,xi)
c=rmi-currm
assert (c%d == 0)
K=c // d *gmpy2.invert(curx//d,xi//d)
currm+=curx*K
curx=curx * xi // d
currm %=curx
return (currm % curx ,curx)
x=[x1,x2,x3,x4]
rm=[rm1,rm2,rm3,rm4]
s,aa=GCRT(x,rm)
s%=n
print(s)
print(libnum.n2s(int(s)))
