1 题目

题源链接
给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置 （索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

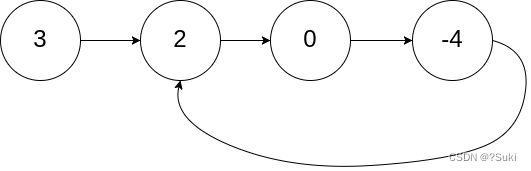
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

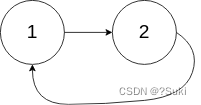
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

提示：

链表中节点的数目范围在范围 [0, 104] 内
-105 <= Node.val <= 105
pos 的值为 -1 或者链表中的一个有效索引

2 思路

这里大家可以去看：Carl老师的视频讲解
思路整理也是摘录Carl老师的代码随想录

这道题目，不仅考察对链表的操作，而且还需要一些数学运算。
主要考察两知识点：

• 判断链表是否环
• 如果有环，如何找到这个环的入口

2.1 判断链表是否有环–快慢指针法

快慢指针法：

分别定义 fast 和 slow 指针，从头结点出发，fast指针每次移动两个节点，slow指针每次移动一个节点，如果 fast 和 slow指针在途中相遇 ，说明这个链表有环。

首先第一点：fast指针一定先进入环中，如果fast指针和slow指针相遇的话，一定是在环中相遇，这是毋庸置疑的。

那么来看一下，为什么fast指针和slow指针一定会相遇呢？

可以画一个环，然后让 fast指针在任意一个节点开始追赶slow指针。

会发现最终都是这种情况， 如下图：

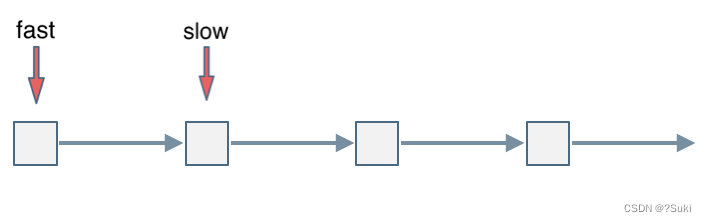
fast和slow各自再走一步， fast和slow就相遇了。

这是因为fast是走两步，slow是走一步，其实相对于slow来说，fast是一个节点一个节点的靠近slow的，所以fast一定可以和slow重合。

动画

2.2 如果有环，如何找到这个环的入口

此时已经可以判断链表是否有环了，那么接下来要找这个环的入口了。

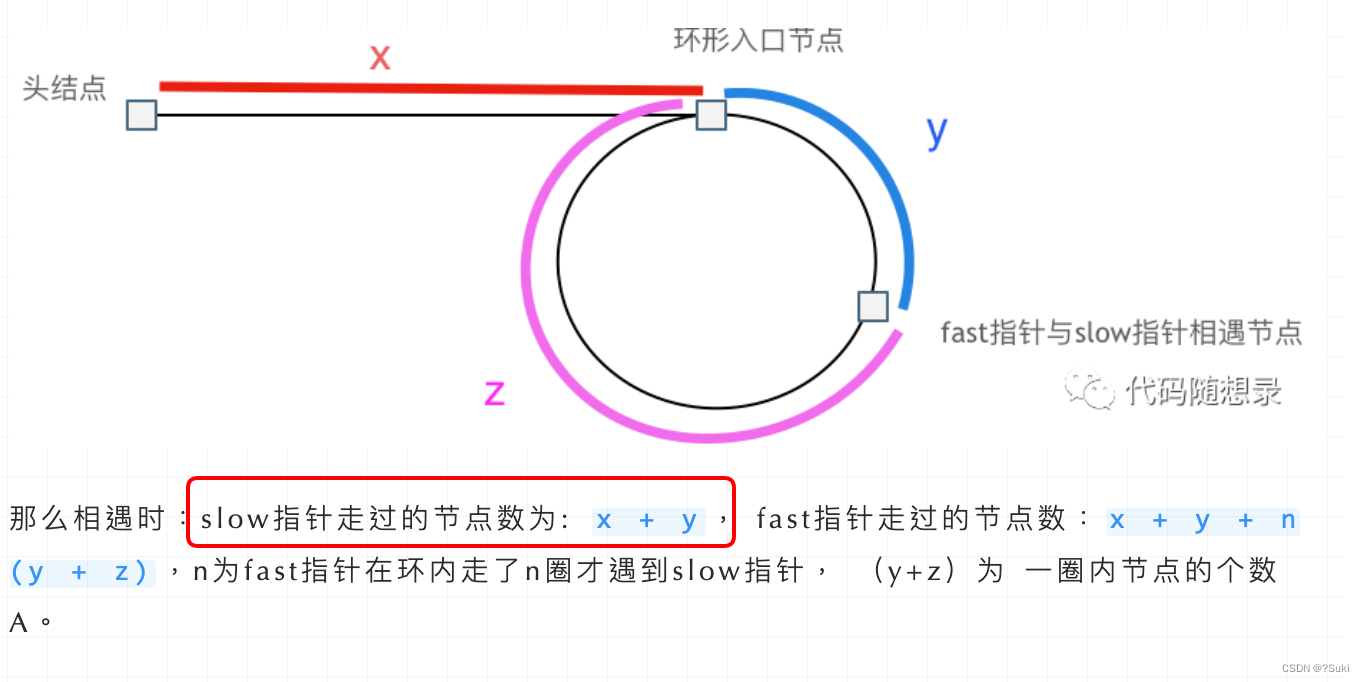
假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。 如图所示：

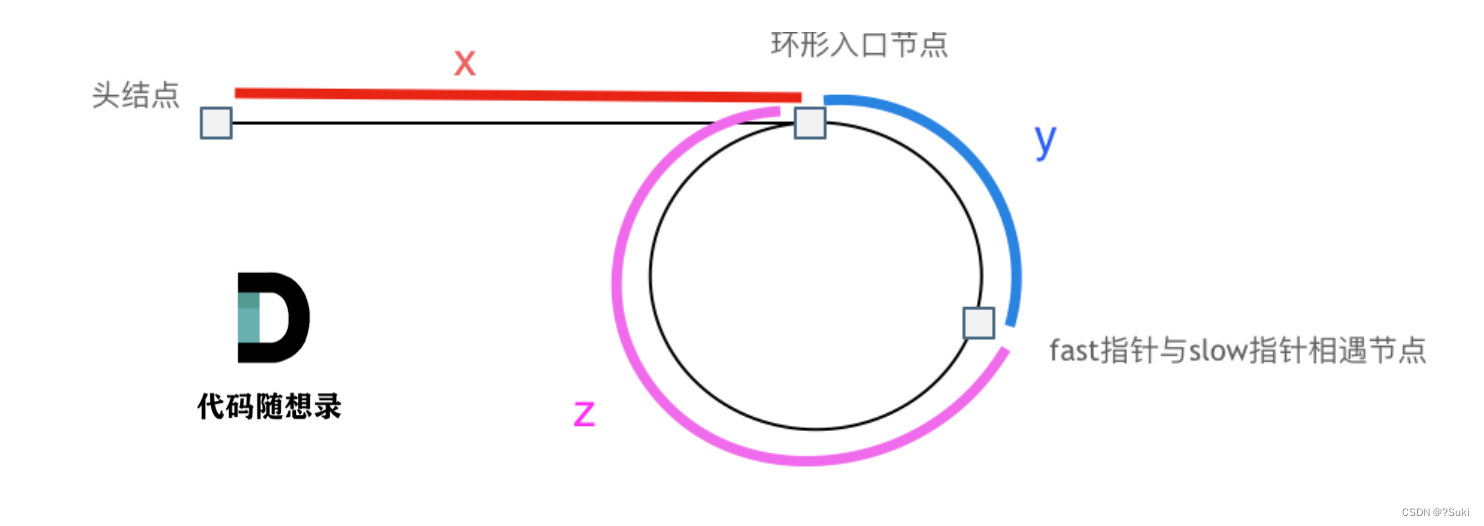
那么相遇时：
slow指针走过的节点数为: x + y，
fast指针走过的节点数：x + y + n (y + z)，
n为fast指针在环内走了n圈才遇到slow指针，
（y+z） 为 一圈内节点的个数A。

因为fast指针是一步走两个节点，slow指针一步走一个节点，
所以 fast指针走过的节点数 = slow指针走过的节点数 * 2：

(x + y) * 2 = x + y + n (y + z)

两边消掉一个（x+y）:
x + y = n (y + z)

因为要找环形的入口，那么要求的是x，因为x表示 头结点到 环形入口节点的的距离。

所以要求x ，将x单独放在左面：
x = n (y + z) - y ,

再从n(y+z)中提出一个 （y+z）来，
整理公式之后为如下公式：
x = (n - 1) (y + z) + z

注意这里n一定是大于等于1的，因为 fast指针至少要多走一圈才能相遇slow指针。

-这个公式说明什么呢？

拿n为1的情况来举例，意味着fast指针在环形里转了一圈之后，就遇到了 slow指针了。

当 n为1的时候，公式就化解为 x = z，

这就意味着，

从头结点出发一个指针，从相遇节点 也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候就是 环形入口的节点。

也就是在相遇节点处，定义一个指针index1，在头结点处定一个指针index2。

让index1和index2同时移动，每次移动一个节点， 那么他们相遇的地方就是 环形入口的节点。
动画

那么 n如果大于1是什么情况呢，就是fast指针在环形转n圈之后才遇到 slow指针。

其实这种情况和n为1的时候 效果是一样的，一样可以通过这个方法找到 环形的入口节点，只不过，index1 指针在环里 多转了(n-1)圈，然后再遇到index2，相遇点依然是环形的入口节点。

2.3 补充

在推理过程中，大家可能有一个疑问就是：
为什么第一次在环中相遇，slow的 步数 是 x+y 而不是 x + 若干环的长度 + y 呢？

首先slow进环的时候，fast一定是先进环来了。

如果slow进环入口，fast也在环入口，那么把这个环展开成直线，就是如下图的样子：

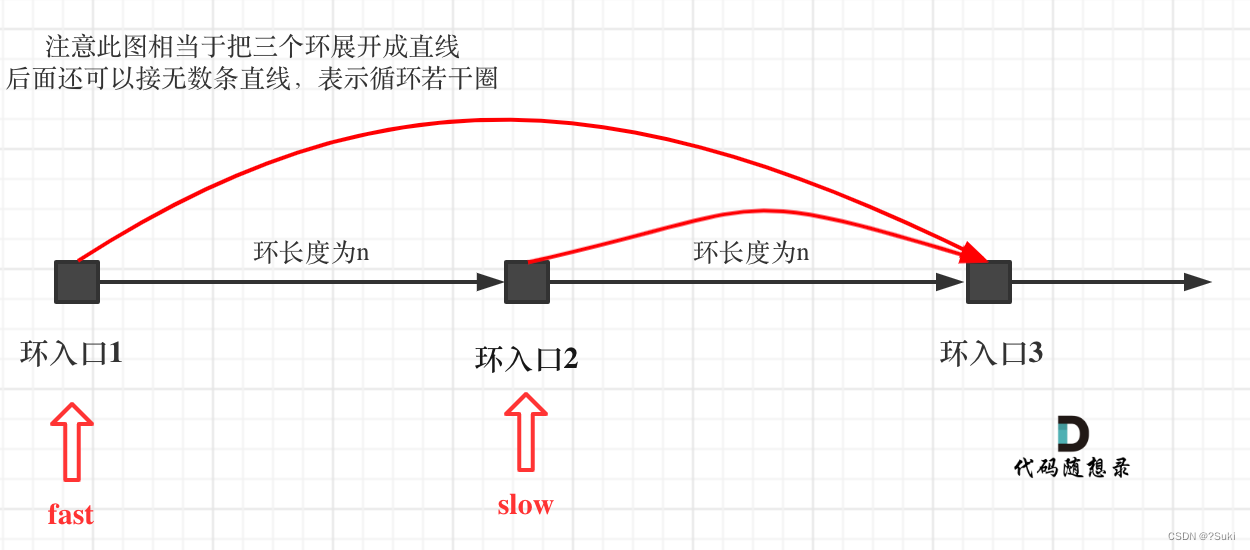
可以看出如果slow 和 fast同时在环入口开始走，一定会在环入口3相遇，slow走了一圈，fast走了两圈。

重点来了，slow进环的时候，fast一定是在环的任意一个位置，如图：

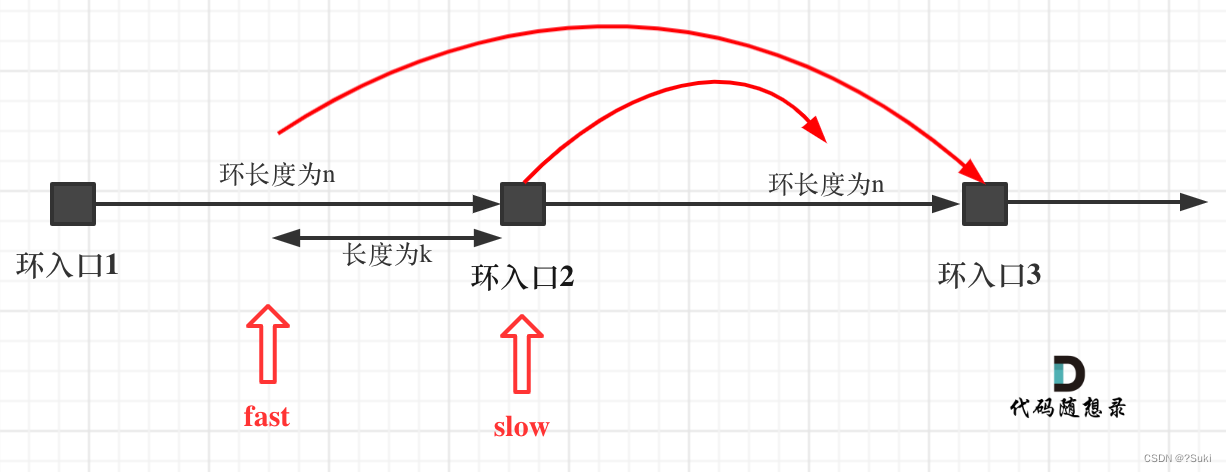
那么fast指针走到环入口3的时候，已经走了k + n 个节点，slow相应的应该走了(k + n) / 2 个节点。

因为k是小于n的（图中可以看出），所以(k + n) / 2 一定小于n。

也就是说 slow一定没有走到环入口3，而fast已经到环入口3了

这说明什么呢？

在slow开始走的那一环已经和fast相遇了。

那有同学又说了，为什么fast不能跳过去呢？ 在刚刚已经说过一次了，fast相对于slow是一次移动一个节点，所以不可能跳过去。

3 代码

3.1 C++版本

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast != NULL && fast->next != NULL) {
            slow = slow->next;
            fast = fast->next->next;
            // 快慢指针相遇，此时从head 和 相遇点，同时查找直至相遇
            if (slow == fast) {
                ListNode* index1 = fast;
                ListNode* index2 = head;
                while (index1 != index2) {
                    index1 = index1->next;
                    index2 = index2->next;
                }
                return index2; // 返回环的入口
            }
        }
        return NULL;
    }
};

3.2 C版本

ListNode *detectCycle(ListNode *head) {
    ListNode *fast = head, *slow = head;
    while (fast && fast->next) {
        // 这里判断两个指针是否相等，所以移位操作放在前面
        slow = slow->next;
        fast = fast->next->next;
        if (slow == fast) { // 相交，开始找环形入口：分别从头部和从交点出发，找到相遇的点就是环形入口
            ListNode *f = fast, *h = head;
            while (f != h) f = f->next, h = h->next;
            return h;
        }
    }
    return NULL;
}

3.3 Java版本

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {// 有环
                ListNode index1 = fast;
                ListNode index2 = head;
                // 两个指针，从头结点和相遇结点，各走一步，直到相遇，相遇点即为环入口
                while (index1 != index2) {
                    index1 = index1.next;
                    index2 = index2.next;
                }
                return index1;
            }
        }
        return null;
    }
}

3.4 JavaScript版本

// 两种循环实现方式
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
// 先判断是否是环形链表
var detectCycle = function(head) {
    if(!head || !head.next) return null;
    let slow =head.next, fast = head.next.next;
    while(fast && fast.next && fast!== slow) {
        slow = slow.next;
        fast = fast.next.next; 
    }
    if(!fast || !fast.next ) return null;
    slow = head;
    while (fast !== slow) {
        slow = slow.next;
        fast = fast.next;
    }
    return slow;
};

var detectCycle = function(head) {
    if(!head || !head.next) return null;
    let slow =head.next, fast = head.next.next;
    while(fast && fast.next) {
        slow = slow.next;
        fast = fast.next.next;
        if(fast == slow) {
            slow = head;
            while (fast !== slow) {
                slow = slow.next;
                fast = fast.next;
            }
            return slow;
        }
    }
    return null;
};

4 总结

主要考察两知识点：

• 判断链表是否环
• 如果有环，如何找到这个环的入口

自己动手推算一遍公式便很好理解啦~
如果还有不懂可以去看Carl老师：

Carl老师的视频讲解
思路整理也是摘录Carl老师的代码随想录

By Suki —2023/1/15