【数据结构与算法】第十八篇：递归，尾递归，尾调用
知识概览
- 一、递归的引入（递归现象）
- 二、递归的调用过程与实例分析
- 三、递归的基本思想
- 小tip:链表递归的具体实例
- 四、递归的一般使用条件
- 五、实例分析：斐波那契数列
- 1.原理剖析
- 2.fib优化1 – 记忆化
- 3.fib优化2
- 4.fib优化3
- 六、实例分析：青蛙跳台阶问题
- 七、实例分析：汉诺塔问题
- 八、递归转非递归分析
- 九、尾调用，尾递归（了解）
- 1. 尾调用的优化（了解）
一、递归的引入（递归现象）
递归思想想必大家都不陌生。它分为“递”和“归”两个过程。是一种常见的算法策略。类似于以下的故事场景：
1.从前有座山，山里有座庙，庙里有个老和尚，正在给小和
尚讲故事呢！故事是什么呢？【从前有座山，山里有座庙，
庙里有个老和尚，正在给小和尚讲故事呢！故事是什么呢？
『从前有座山，山里有座庙，庙里有个老和尚，正在给小
和尚讲故事呢！故事是什么呢？……』】
2.GNU 是 GNU is Not Unix 的缩写
GNU → GNU is Not Unix → GNU is Not Unix is Not Unix → GNU is Not Unix is Not Unix is Not Unix
3.假设A在一个电影院，想知道自己坐在哪一排，但是前面人很多，
A 懒得数，于是问前一排的人 B【你坐在哪一排？】，只要把 B 的答案加一，就是 A 的排数。
B 懒得数，于是问前一排的人 C【你坐在哪一排？】，只要把 C 的答案加一，就是 B 的排数。
C 懒得数，于是问前一排的人 D【你坐在哪一排？】，只要把 D 的答案加一，就是 C 的排数。
…
二、递归的调用过程与实例分析
以下面这段代码为例
/**
* 计算n的阶乘
* 1*2*3*4......*(n-1)*n
*/
public int Fac(int n){
if(n<=1)return n;
return n*Fac(n-1);
}
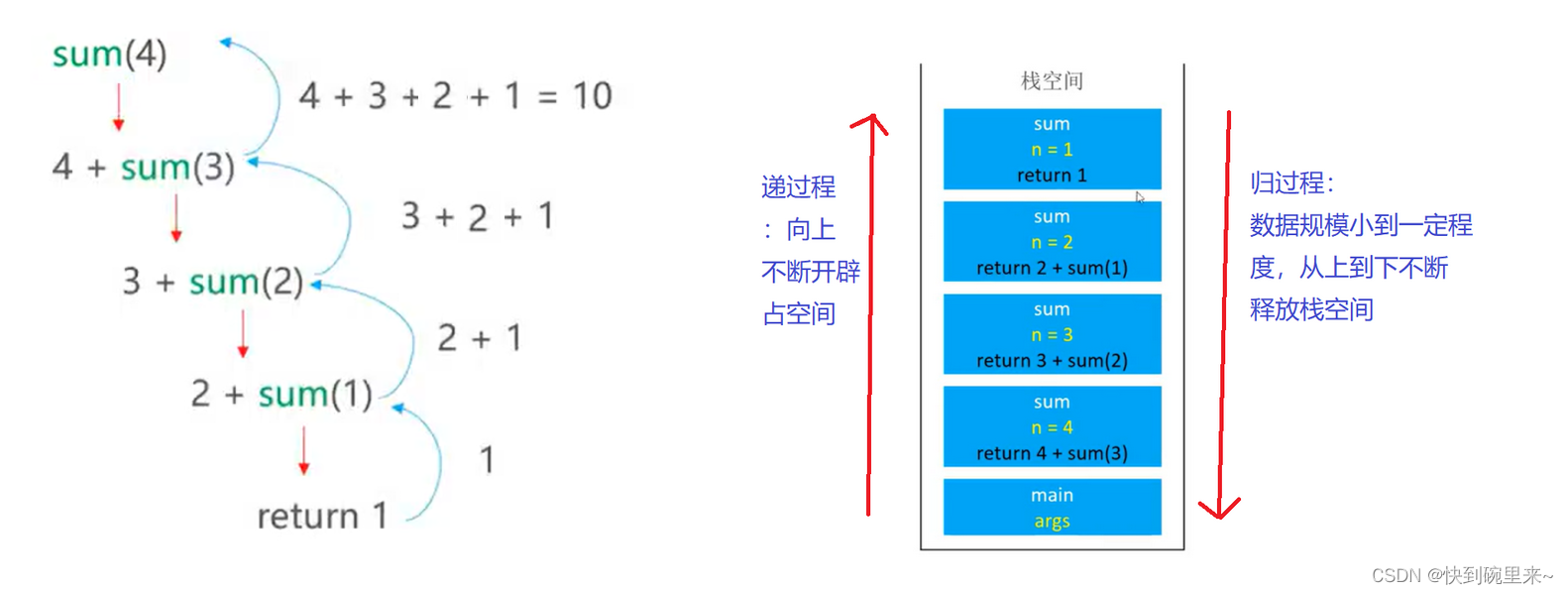
时间，空间复杂度分析
递归所需要的时间：T(n)=T(n-1)+O(1)
根据时间对应表如下：
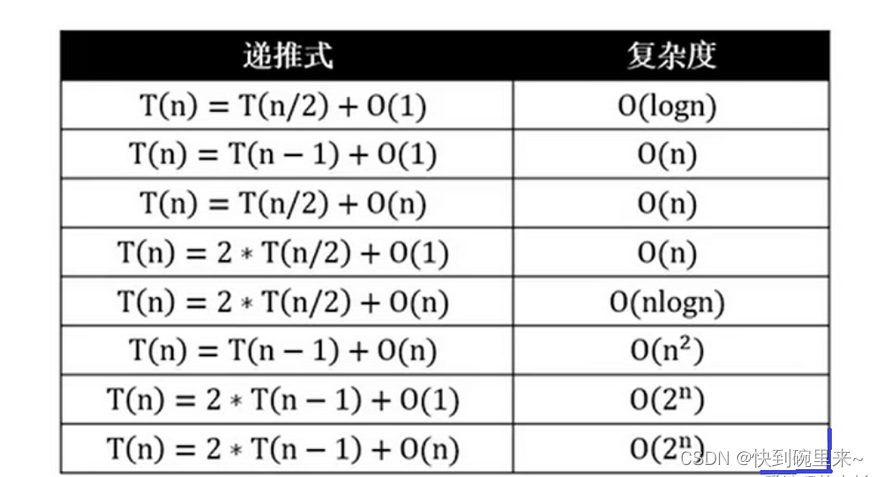可以得出时间复杂度为 : O(n)
空间复杂度为: O(n) (开辟了n个占空间)
几种优化思想
三、递归的基本思想
拆解思想
1.把规模较大的问题转化为同类型的规模较小的问题。
2.把规模较小的问题转化为规模更小的问题。
3.规模较小的问题可以直接得出他的答案。
求解
1.由最小规模问题的解得出较大规模问题的解
2.由较大规模问题的解不断得出规模更大问题的解
3.最后得出原来问题的解
这两种思想正好体现了递归的 ‘递’和‘归’两个过程
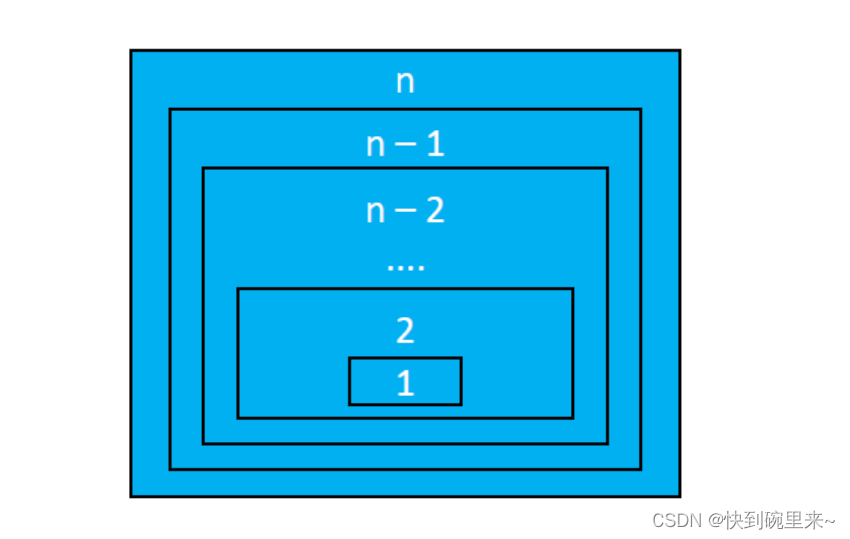类似于可以利用上面这种思想解题的都可以考虑递归，递归不是为了得到最优解,而是为了简化解题思想。
很多链表、二叉树相关的问题都可以使用递归来解决
✓ 因为链表、二叉树本身就是递归的结构（链表中包含链表，二叉树中包含二叉树）
小tip:链表递归的具体实例
2.两数相加
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
if(l1==null)return l2;
if(l2==null)return l1;
int sum=l1.val+l2.val;
ListNode head=new ListNode(sum%10);
head.next=addTwoNumbers(l1.next,l2.next);
if(sum>9)head.next=addTwoNumbers(head.next,new ListNode(1));
return head;
}
}
四、递归的一般使用条件
① 明确函数的功能 (重要！！！)
先不要去思考里面代码怎么写，首先搞清楚这个函数的干嘛用的，能完成什么功能？
② 明确原问题与子问题的关系
寻找 f(n) 与 f(n – 1) 的关系
③ 明确递归基（边界条件）
递归的过程中，子问题的规模在不断减小，当小到一定程度时可以直接得出它的解
重要：寻找递归基，相当于是思考：问题规模小到什么程度可以直接得出解？
五、实例分析：斐波那契数列
斐波那契数列：1、1、2、3、5、8、13、21、34、……
F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n≥3）
◼ 编写一个函数求第 n 项斐波那契数
以上写法的空间复杂度为O（n）.
你可能会疑惑为什么双路递归那么重复调用，为什么空间复杂度才O(n)级别，而时间复杂度却达到了恐怖的O(2n)?这里我们先抛出一个计算递归空间复杂度复杂度的通式
递归调用的空间复杂度=递归深度*每次递归调用所需要的辅助空间。
具体原理我们下文细细剖析~
1.原理剖析
根据以上的复杂度分析，对于斐波那契这种多路递归，时间复杂度为O(2n),这个时间复杂度是十分恐怖的。双路递归不可避免的重复计算很多。
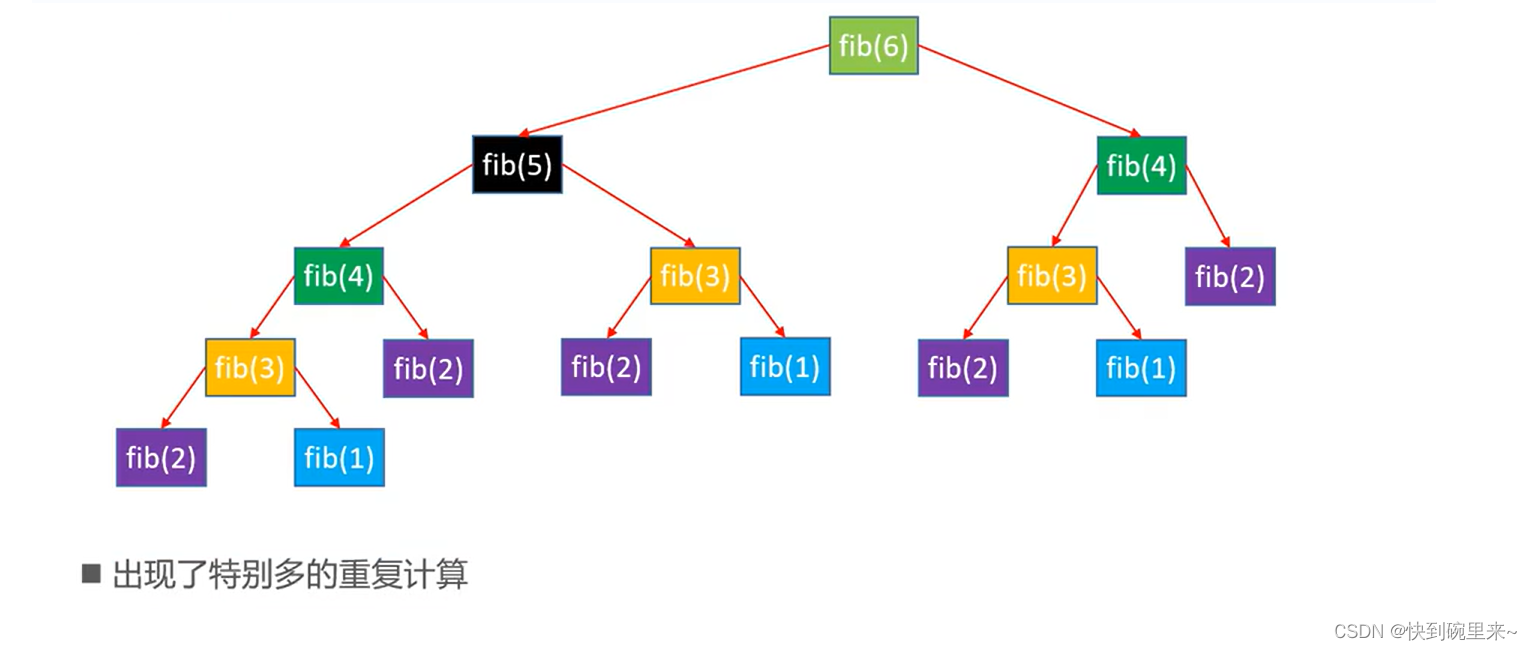
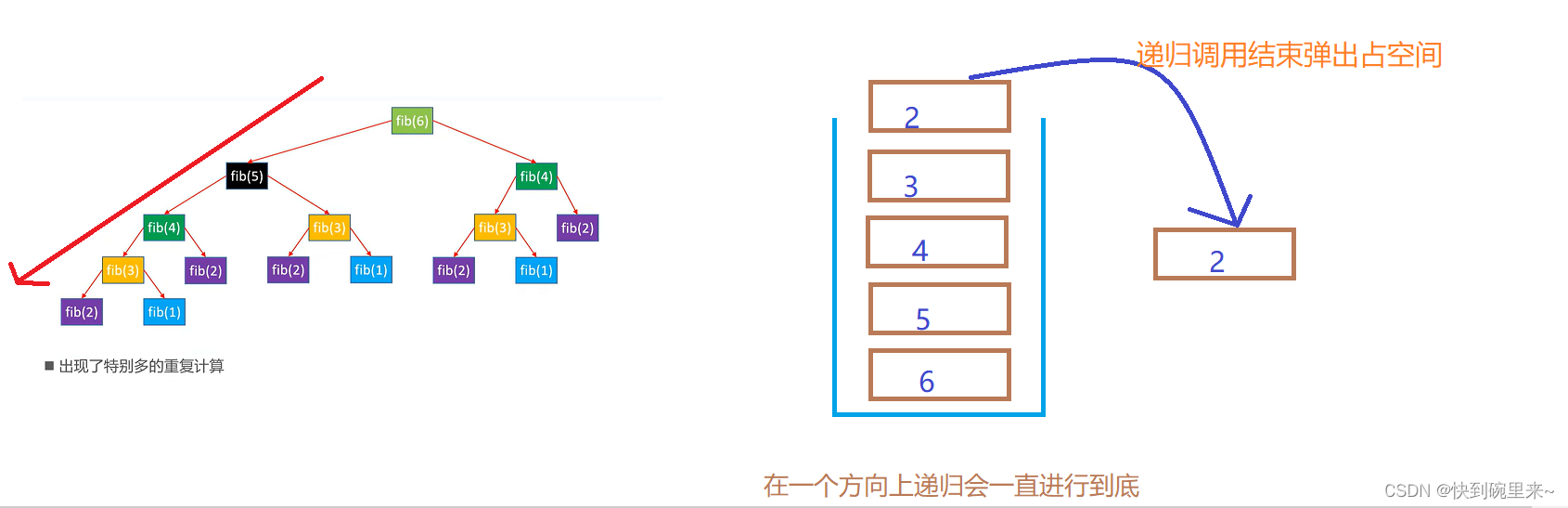
2.fib优化1 – 记忆化
在上面的介绍种，斐波那契额数列性能差的一个重要因素就是拥有大量的重复计算。
假如我们从根节点向着一个方向先进行递归，记住已经算过的递归调用的返回值
然后在进行另一个分支计算时就不用再次进行重复计算了，大大减少了重复计算。我们用数组来实现这个思想。
public static int fib2(int n){
if(n<=2)return 1;
int [] array=new int [n+1];
array[1]=array[2]=1;
return fib3(n,array);
}
public static int fib3(int n,int []array){
if(array[n]==0){//说明该位置还没有赋值
array[n]=fib3(n-1,array)+fib3(n-2,array);
}
return array[n];
}
}
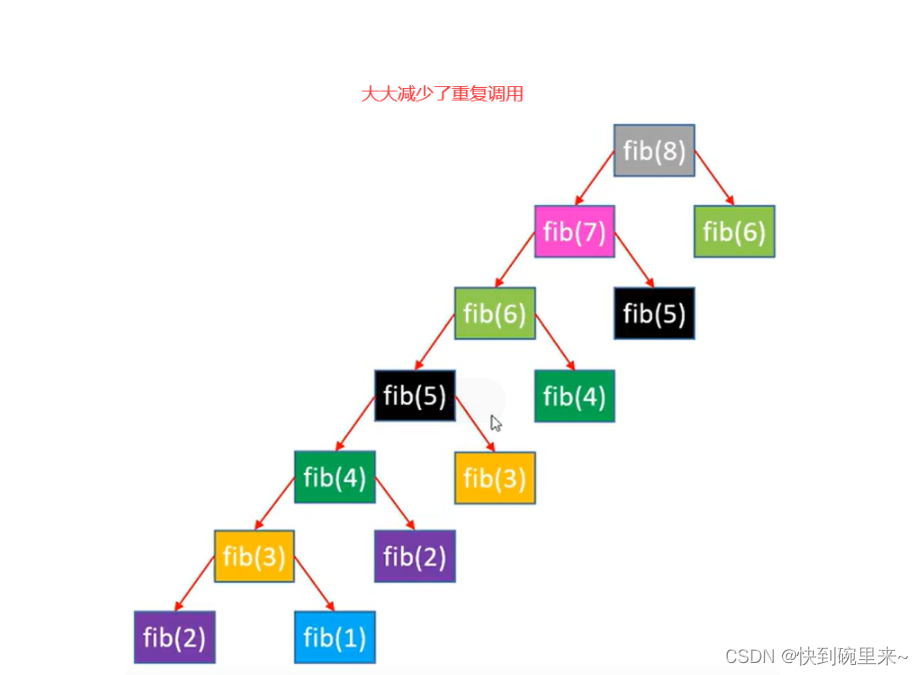
◼ 时间复杂度：O(n)，空间复杂度：O(n)
3.fib优化2
去除递归操作
//去除递归优化时间复杂度O(n)
public static int fib1(int n){
int [] array=new int[n+1];
array[1]=array[2]=1;
for(int i=3;i<=n;i++){
array[i]=array[i-1]+array[i-2];
}
return array[n];
}
4.fib优化3
由于每次运算只需要用到数组中的 2 个元素，所以可以使用滚动数组来优化,创建一个空间为2的数组每次，依次向下更新数组元素的值。
这里的&运算符就是%运算符的作用。
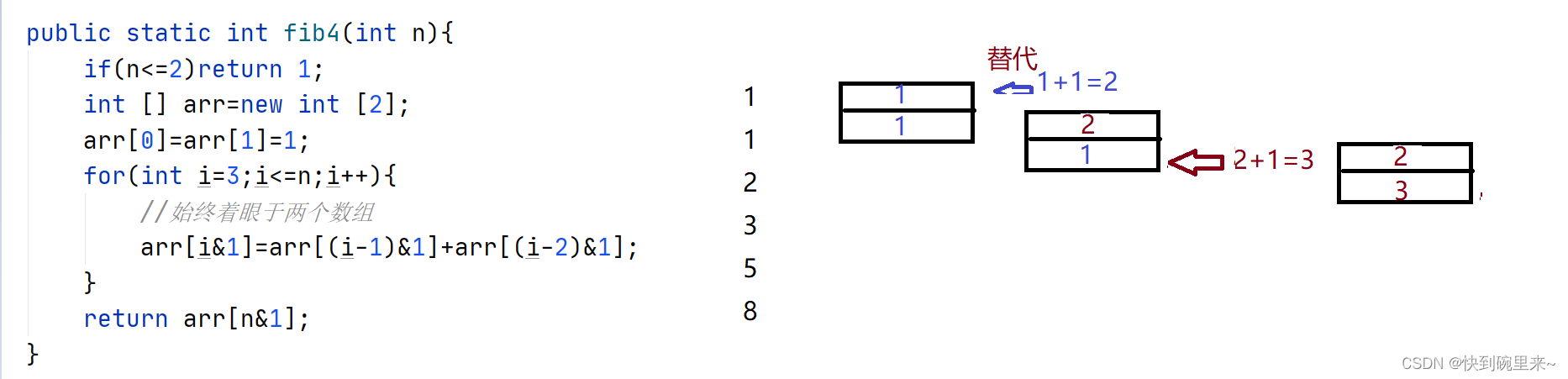
public static int fib4(int n){
if(n<=2)return 1;
int [] arr=new int [2];
arr[0]=arr[1]=1;
for(int i=3;i<=n;i++){
//始终着眼于两个数组
arr[i&1]=arr[(i-1)&1]+arr[(i-2)&1];
}
return arr[n&1];
}
//上台阶
public static int f(int n){
if(n<=2)return n;
return f(n-1)+f(n-2);
}
这里为什么可以用&取代%（%2都可以改成&1）
六、实例分析：青蛙跳台阶问题
楼梯有 n 阶台阶，上楼可以一步上 1 阶，也可以一步上 2 阶，走完 n 阶台阶共有多少种不同的走法？
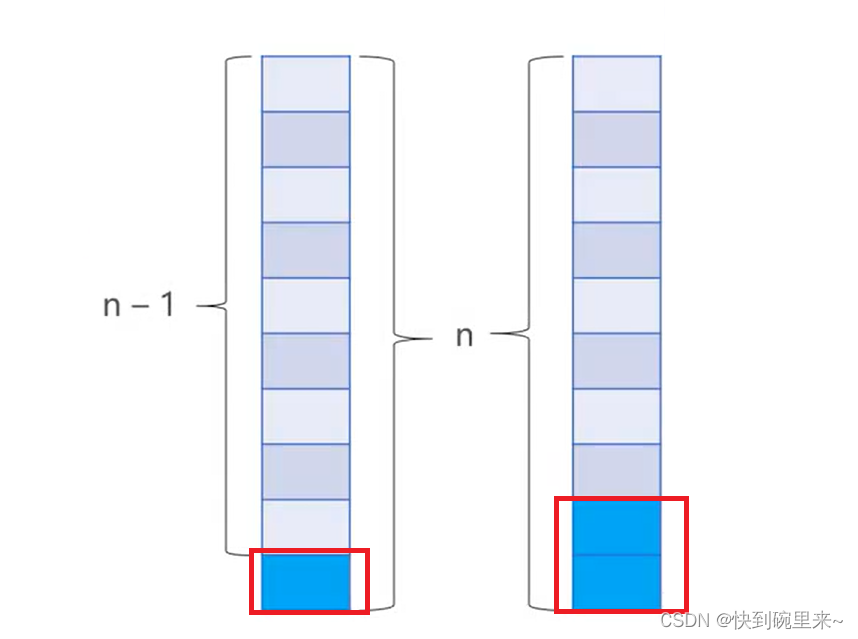
√假设 n 阶台阶有 f(n) 种走法，第 1 步有 2 种走法
✓ 如果上 1 阶，那就还剩 n – 1 阶，共 f(n – 1) 种走法
✓ 如果上 2 阶，那就还剩 n – 2 阶，共 f(n – 2) 种走法
√所以 f(n) = f(n – 1) + f(n – 2)
public int climbStairs(int n){
if(n<=2)return n;
return climbStairs(n-1)+climbStairs(n-2);
}
迭代优化
public int climbStairs1(int n){
if(n<=2)return n;
int first=1;
int second=2;
for(int i=3;i<=n;i++){
second=first+second;
first=second-first;
}
return second;
}
七、实例分析：汉诺塔问题
编程实现把 A 的 n 个盘子移动到 C（盘子编号是 [1, n] ）
1.每次只能移动1个盘子
2.大盘子只能放在小盘子下面
递归的基本思想，找到递归是条件
最初的思想是将n个木盘从A移动到C，B作为中间过渡柱子。
现在可以找到共同性（1）先将n-1个柱子从A移动到B，C作为中间过渡柱子。
（2）然后再将第n个柱子移动到C.（3）然后再将n-1个柱子从B移动到C，A最为中间过渡柱子。
找到则会个规律我们用代码来实现以下。
/**
* 柱子p1 p2 p3
* 木板：
* 1
* 2
* 3
* 4
* .......
* n-1
* n
* 按位置来说：p1:起始位置 p2:中间过渡位置 p3:最终位置
*
*/
//找到递归规律
public static void hanoi(int n,String p1,String p2,String p3){
//就一块板子
if(n==1){
move(n,p1,p3);
return;
}
hanoi(n-1,p1,p3,p2);
move(n,p1,p3);
hanoi(n-1,p2,p1,p3);
}
public static void move(int n,String from,String to){
System.out.println("将"+n+"号盘子从"+from+"移动到"+to);
}
八、递归转非递归分析
递归分为递和归两个过程，所以再递的过程中，先一直向更深的方向递归，然后数据规模小到一定程度，直接返回一个数然后递归的空间按时间开辟晚到近依次释放。这和栈的先进后出的特点十分相似。不出所料递归的底层也是通过栈实现的，所以一般递归都可以通过栈转化为非递归。
实例一：递归形式
public void log(int n){
if(n<1)return;
log(n-1);
int v=n+10;
System.out.println(v);
}
非递归实现（创建辅助对象）
//非递归实现
public void log1(int n){
Stack<Model> stack=new Stack<>();
while(n>0){
stack.push(new Model(n,n+10));
n--;
}
while(!stack.isEmpty()){
System.out.println(stack.pop().getV());
}
}
package Test01;
public class Model {
private int n;
private int v;
public Model(int n, int v) {
this.n = n;
this.v = v;
}
public int getN() {
return n;
}
public void setN(int n) {
this.n = n;
}
public int getV() {
return v;
}
public void setV(int v) {
this.v = v;
}
}
九、尾调用，尾递归（了解）
◼ 尾调用：一个函数的最后一个动作是调用函数
◼如果最后一个动作是调用自身，称为尾递归（Tail Recursion），是尾调用的特殊情况
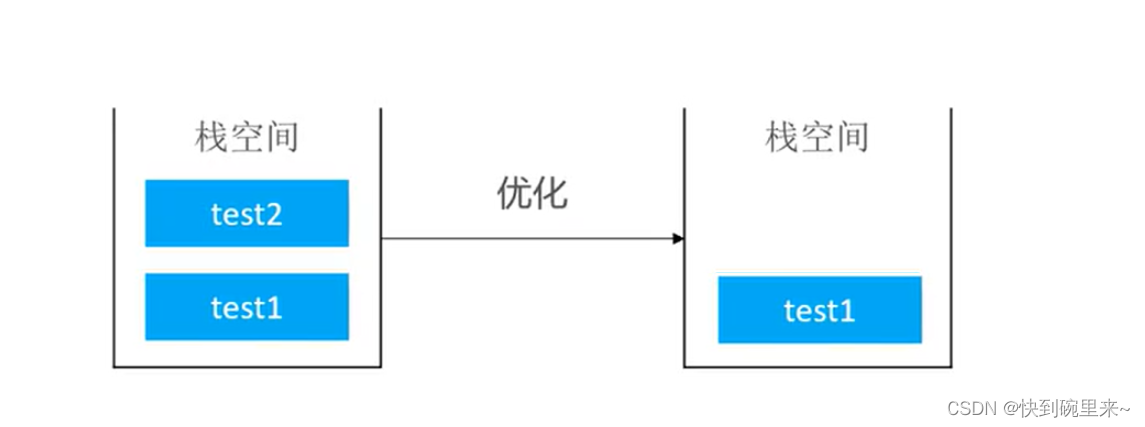
◼ 一些编译器能对尾调用进行优化，以达到节省栈空间的目的（但是java编译器并不支持）
上面图中的代码为例，按照代码中的调用应该会向上不断开辟空间，但是如果是尾调用优化的话则不会在想上开辟空间直接重复利用test1的空间。
那么问题来了：如果是尾递归肯定没得说，每次调用的栈空间肯定是相同大小的，如果是尾调用，调用其他方法，栈空间不一样大怎么办？
答：这个大可不必担心，因为，某些编译器的底层会对其在原有基础上进行扩容。
尾调用判断
}
/**
* 计算n的阶乘
* 1*2*3*4......*(n-1)*n
*/
public int Fac(int n){
if(n<=1)return n;
return n*Fac(n-1);
}
这个不是尾调用因为，最后一步执行的是*，而不是调用函数。
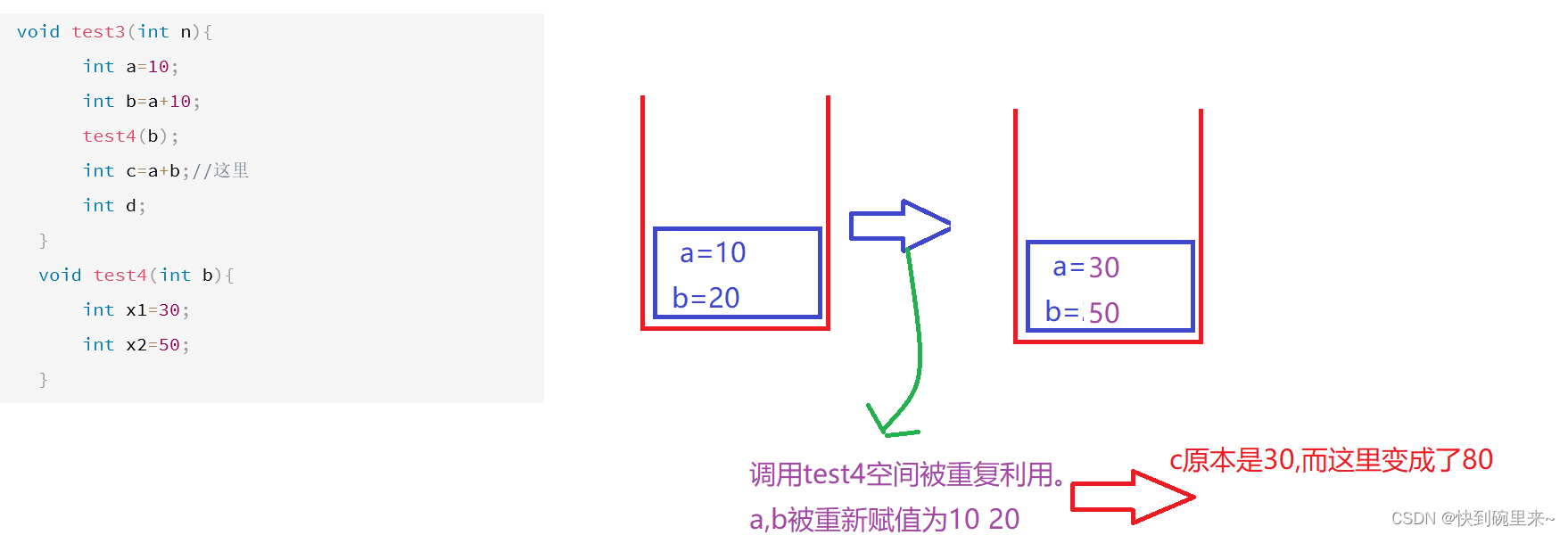
void test3(int n){
int a=10;
int b=a+10;
test4(b);
int c=a+b;//这里
int d;
}
void test4(int b){
int x1=30;
int x2=50;
}
不是尾调用，只有最后一句是调用函数的时候才是尾调用
为什么只有最后一句是尾调用的时候才是尾调用？
一上面这段代码为例。
1. 尾调用的优化（了解）
实例一：n的阶乘改成非递归
//改成尾调用优化
public int Fac1(int n) {
return Fac2(n,1);
}
public int Fac2(int n,int result){
if(n<=1)return n;
//result:之前的结果
return Fac2(n-1,result*n);
}
实例二：斐波那契改成非递归
//斐波那契实现为调用
public int Fib(int n){
return Fib1(n,1,1);
}
public int Fib1(int n,int first,int second){
if(n<=1)return first;
return Fib1(n-1,second,first+second);
}
