0 写在前面

机器学习强基计划聚焦深度和广度，加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理；“广”在分析多个机器学习模型：决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。强基计划实现从理论到实践的全面覆盖，由本人亲自从底层编写、测试与文章配套的各个经典算法，不依赖于现有库，可以大大加深对算法的理解。

🚀详情：机器学习强基计划(附几十种经典模型源码)

在机器学习强基计划6-2：详细推导马尔科夫随机场(MRF)及其应用(附例题)中我们系统地介绍了引入马尔科夫随机场的动机及其基本概念，但由于公式繁多，很难理解这个模型如何应与实际相结合，本文结合一个计算机视觉领域的经典问题——图像分割讲解马尔科夫随机场的应用，加深对概率图模型的理解。为了便于说明，先引入计算机视觉中的部分概念。

1 图像分割问题

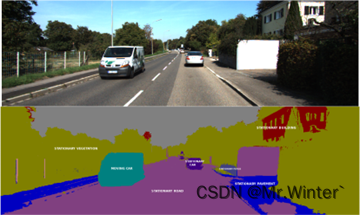
在图像处理与计算机视觉领域，图像分割(image segmentation)是在像素级别将一个完整图像划分为若干具有特定语义区域(region)或对象(object)的过程。每个分割区域是一系列拥有相似特征——例如颜色、强度、纹理等的像素集合，因此图像分割也可视为以图像属性为特征空间，为全体像素赋予标签的分类问题。

图像分割是高级图像处理的基础技术，它将原始冗余而繁杂的图像，转化为一种更具意义且简单紧凑的组织形式。在智能安防、卫星遥感、医学影像处理、生物特征识别等领域，图像分割通过提供精简且可靠的图像特征信息，有效地提高后续从而利于后续图像分析、理解等技术的计算效率，具有重要意义。

2 图像像素邻域

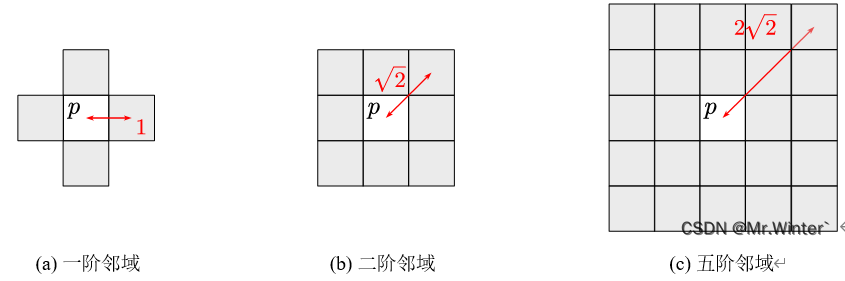
在图像分割中，通常默认图像中某像素点$p\left(i,j\right)$只受相邻像素的影响，较远处的像素对该像素没有作用，或者说其作用已被包含在相邻像素内

例如当前像素语义是天空，那么近邻像素也很可能表示天空。

形式化地，像素$p$的邻域定义为

$${\delta }_d\left(p\right)=\left\{q\in R|\mathrm{dist}\left(p,q\right)⩽\sqrt{d},d\in {\mathbb{N}}^{+},q\ne p\right\}$$

其中$\mathrm{dist}\left(\cdot ,\cdot \right)$表示两个像素间的欧式距离，$d$表示的是邻域的阶次，阶次越高像素包含的邻点越多，且满足当阶次$t>d$时${\delta }_d\left(p\right)\subset {\delta }_t\left(p\right)$

这种邻域特性类似于马尔科夫链的无后效性，参考机器学习强基计划6-1：图文详细总结马尔科夫链及其性质(附例题分析)。由于图像是二维数据，因此用经典的无向图模型——马尔科夫随机场代替一维的马尔科夫链进行建模。马尔科夫随机场中的全局马尔科夫性、局部马尔科夫性和成对马尔科夫性，恰好表征了像素只受邻域影响的假设偏好。

3 观测场与标记场

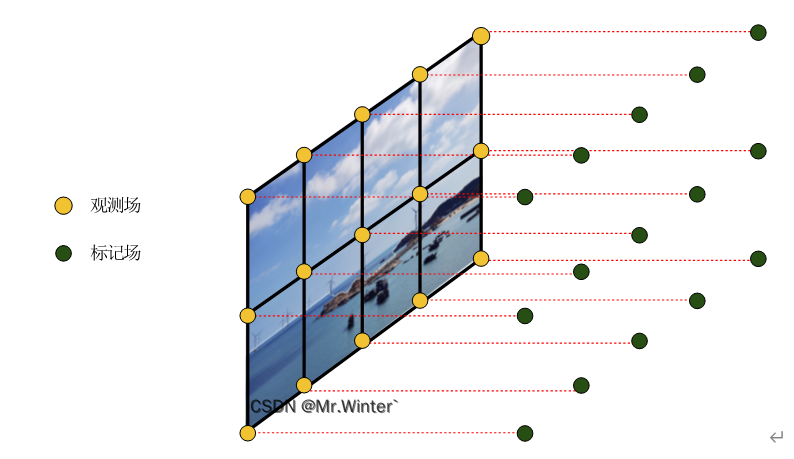
进行图像分割时，需要定义两个随机场：

• 观测场$Y$：指肉眼可见的图像实际像素场
• 标记场$X$：每个可观测像素都赋予一个标记，这些标记组成标记场。这两个随机场一一对应
  

形式化地，设观测场

Y = { y ∣ y ∈ R } Y=\left\{ y|y\in R \right\} Y={y∣y∈R}

其中$y$是图像每个像素的真实取值。标记场

X = { x p ∣ p ∈ R , x p ∈ R } X=\left\{ x_p|p\in R, x_p\in \mathcal{R} \right\} X={xp​∣p∈R,xp​∈R}

其中$x_p$表示像素$p$被赋予的分割区域，总共有$\left|\mathcal{R}\right|$种可能的分割情形。

图像分割的目标是在已有观测图像的情况下，让标记场的概率最大，根据极大后验估计可得

$$\begin{array}{rl}X& =\arg \underset{X}{\max }P\left(X|Y\right)\\ & =\arg \underset{X}{\max }P\left(X\right)P\left(Y|X\right)\\ & =\arg \underset{X}{\max }\left(\ln P\left(X\right)+\ln P\left(Y|X\right)\right)\end{array}$$

为了求解这个优化目标，分别对$P(X)$和$P(Y|X)$建模。

4 马尔科夫随机场建模

根据机器学习强基计划6-2：详细推导马尔科夫随机场(MRF)及其应用(附例题)的讲解，我们可以用马尔科夫随机场对联合分布$P(X)$建模，列出

$$P\left(X\right)=\frac{1}{Z^{\ast }}\prod _{Q\in {\mathcal{C}}^{\ast }}{\varphi }_Q\left({\mathbf{D}}_Q\right)=\frac{1}{Z^{\ast }}\prod _{Q\in {\mathcal{C}}^{\ast }}{e}^{-{\sum }_{u,v\in Q,u\ne v}{\beta }_{uv}\mathbb{I}\left(x_u\ne x_v\right)}$$

这里令能量函数

$$H_Q\left({\mathbf{D}}_Q\right)=\sum _{u,v\in Q,u\ne v}{\beta }_{uv}\mathbb{I}\left(x_u\ne x_v\right)$$

称为Potts马尔科夫随机场，倾向于两个相邻像素取值相同，当相邻像素不等时，整体能量会上升，比如一个表示天空的蓝色像素，我们更倾向于和它属于同一类的像素都是蓝色的。

$P(Y|X)$表示了像素与其标签的匹配程度，可用高斯分布建模

$$P\left(Y|X\right)=\prod _{y\in R}P\left(y|x_y\right)=\prod _{y\in R}\frac{1}{\sqrt{2\pi }{\sigma }_{x_y}}\exp \left[-\frac{{\left(y-{\mu }_{x_y}\right)}^2}{2{\sigma }_{x_y}^2}\right]$$

这里的均值和方差通过图像数据集训练得到，所以这个高斯概率模型就代表了通常意义下某个类的像素分布情况。比如说我们选择一百张标记好的图像，把这些图像中代表天空的像素进行累加，然后求平均就是这里的均值；方差同理

综合$P(X)$和$P(Y|X)$，可以得到优化目标

$$\begin{array}{rl}X& =\arg \underset{X}{\max }P\left(X|Y\right)\\ & =\arg \underset{X}{\max }P\left(X\right)P\left(Y|X\right)\\ & =\arg \underset{X}{\max }\left(\ln P\left(X\right)+\ln P\left(Y|X\right)\right)\\ & =\arg \underset{X}{\min }\left[\sum _{Q\in {\mathcal{C}}^{\ast }}\sum _{u,v\in Q,u\ne v}{\beta }_{uv}\mathbb{I}\left(x_u\ne x_v\right)+\sum _{y\in R}\left(\sqrt{2\pi }{\sigma }_{x_y}+\frac{{\left(y-{\mu }_{x_y}\right)}^2}{2{\sigma }_{x_y}^2}\right)\right]\end{array}$$

用这个目标定义损失函数

$$U\left(X\right)=\sum _{Q\in {\mathcal{C}}^{\ast }}\sum _{u,v\in Q,u\ne v}{\beta }_{uv}\mathbb{I}\left(x_u\ne x_v\right)+\sum _{y\in R}\left(\sqrt{2\pi }{\sigma }_{x_y}+\frac{{\left(y-{\mu }_{x_y}\right)}^2}{2{\sigma }_{x_y}^2}\right)$$

采用模拟退火等方法可以求得近似最优解。

5 Python实现

5.1 计算能量函数

能量函数的定义参加第四节的Potts马尔科夫随机场

def __calEnergy(self, label: int, index: tuple, img: np.ndarray, w: np.ndarray) -> float:
    # get image's shape
    channels = 0
    try:    rows, cols, channels = img.shape
    except: rows, cols = img.shape

    i, j = index
    energy = 0.0
    
    if channels:
        for c in range(channels):
            val = img[i][j][c]
            mean, var = self.class_info[label][c][1], self.class_info[label][c][2]
            energy += np.log(np.sqrt(2 * np.pi * var)) + ((val - mean)**2) / (2 * var)
    else:
        val = img[i][j]
        mean, var = self.class_info[label][0][1], self.class_info[label][0][2]
        energy += np.log(np.sqrt(2 * np.pi * var)) + ((val - mean)**2) / (2 * var)

    # clique energy(Potts model)
    neighbor = [[0, 1], [0, -1], [1, 0], [-1, 0]]
    for dx, dy in neighbor:
        if 0 <= i + dx < rows and 0 <= j + dy < cols:
            energy = energy + self.beta_ if label == w[i + dx][j + dy] else energy

    return energy 

5.2 退火优化

while (iteration < 500):
	# try new label
	x, y = random.randint(0, rows - 1), random.randint(0, cols - 1)
	labels = [i for i in range(len(self.class_info))]
	labels.remove(w[x][y])
	new_label = labels[random.randint(0, len(labels) - 1)]
	
	# delta energy between old label and new label
	delta = self.__calEnergy(new_label, (x, y), img, w) - self.__calEnergy(w[x][y], (x, y), img, w)
	if (delta <= 0):
	    w[i][j] = new_label
	    energy += delta
	else:
	    p = -delta / current_temp
	    if random.uniform(0, 1) < p:
	        w[i][j] = new_label
	        current_energy += delta
	current_temp *= 0.95
	iteration += 1

5.3 效果展示

本文完整工程代码请联系下方博主名片获取

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《机器人原理与技术》
• 《机器学习强基计划》
• 《计算机视觉教程》
• …