1.数组

（1）找到所有数组中消失的数字(448)

给你一个含 n 个整数的数组 nums ，其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字，并以数组的形式返回结果。

输入：nums = [4,3,2,7,8,2,3,1]
输出：[5,6]

输入：nums = [1,1]
输出：[2]

//时间空间复杂度都为O(n)
public class Solution {

    public static void main(String[] args) {
        int[] arr={4,3,2,7,8,2,3,1};
        Solution solution=new Solution();
        System.out.println(solution.findDisappearedNumbers(arr));
    }

    public List<Integer> findDisappearedNumbers(int[] nums) {
        int n= nums.length;
        boolean[] find=new boolean[n+1];//数组中出现的数将该数对应的数组位置置为true
        List<Integer> list=new ArrayList<>();
        for (int i=0;i<n;i++){
            find[nums[i]]=true;
        }
        for (int i=1;i<=n;i++){
            if (!find[i]){
                list.add(i);
            }
        }
        return list;
    }
}


//空间复杂度为O(1)
public class Solution {

    public static void main(String[] args) {
        int[] arr={4,3,2,7,8,2,3,1};
        Solution solution=new Solution();
        System.out.println(solution.findDisappearedNumbers(arr));
    }

    public List<Integer> findDisappearedNumbers(int[] nums) {
        int n= nums.length;
        List<Integer> list=new ArrayList<>();
        //遍历数组 每遇到一个数x 就让nums[x-1]增加n
        //当我们遍历到某个位置时 其中的数可能已经被增加过了 因此需要对n取模
        for (int i=0;i<n;i++){
            int x=(nums[i]-1)%n;
            nums[x]+=n;
        }
        //遍历nums 若nums[i]未大于n 就说明没有遇到过数i+1
        for (int i=0;i<n;i++){
            if (nums[i]<=n){
                list.add(i+1);
            }
        }
        return list;
    }
}

（2）旋转图像(48)

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

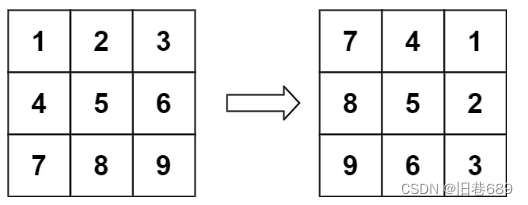
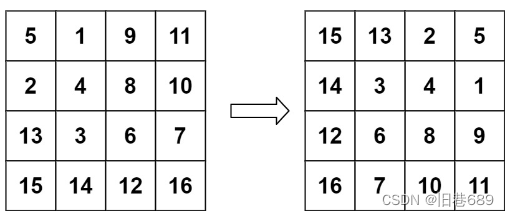
对应位置交换位置，结束条件可以考虑i和j同时向内缩进，也就是一圈一圈考虑

public class Solution {

    public static void main(String[] args) {
        int[][] arr={{5,1,9,11},
                     {2,4,8,10},
                     {13,3,6,7},
                     {15,14,12,16}};
        Solution solution=new Solution();
        solution.rotate(arr);
        for (int i=0;i<arr.length;i++){
            for (int j=0;j< arr[0].length;j++){
                System.out.print(arr[i][j]+" ");
            }
            System.out.println();
        }
    }

    public void rotate(int[][] matrix) {
        int rowMin=0;//从第0行开始 起始行
        int colMin=0;//从第0列开始 起始列
        int rowMax= matrix.length-1;//第一圈可以用到的的最大行数是总行数-1
        int colMax=matrix[0].length-1;//第一圈可以用到的的最大列数是总列数-1
        //旋转完一圈开始下一圈 循环退出条件是 起始行>最大行 起始列>最大列
        while (rowMin<=rowMax&&colMin<=colMax){
            RotateOneCircle(matrix,rowMin,colMin,rowMax,colMax);
            //缩进
            rowMin++;
            colMin++;
            rowMax--;
            colMax--;
        }
    }

    //旋转一圈的方法
    private void RotateOneCircle(int[][] arr, int rowMin, int colMin, int rowMax, int colMax) {
        int temp=0;//辅助数
        //遍历旋转这一圈
        for (int j=0;j<colMax-colMin;j++){
            temp=arr[rowMin][colMin+j];
            arr[rowMin][colMin+j]=arr[rowMax-j][colMin];
            arr[rowMax-j][colMin]=arr[rowMax][colMax-j];
            arr[rowMax][colMax-j]=arr[rowMin+j][colMax];
            arr[rowMin+j][colMax]=temp;
        }
    }
}

（3）搜索二维矩阵 II(240)

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

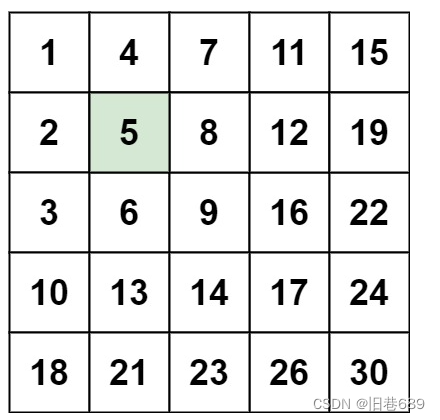
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

从数组的右上角开始遍历，如果target大于当前元素，则用当前元素下方的元素再次比较；如果target小于当前元素，
则用当前元素左边的元素再次比较；以此类推，知道找到target或者到达边界

public class Solution {

    public static void main(String[] args) {
        int[][] arr={{1,4,7,11,15},
                     {2,5,8,12,19},
                     {3,6,9,16,22},
                     {10,13,14,17,24},
                     {18,21,23,26,30}};
        int target=5;
        Solution solution=new Solution();
        System.out.println(solution.searchMatrix(arr,5));
    }

    public boolean searchMatrix(int[][] matrix, int target) {
        int m= matrix.length;
        int n=matrix[0].length-1;//表示列
        int i=0;//表示行
        while (i<m&&n>=0){
            if (target>matrix[i][n]){//target大于当前元素 比较下方元素
                i++;
            } else if (target<matrix[i][n]) {//target小于当前元素 比较左方元素
                n--;
            }else {//找到target
                return true;
            }
        }
        return false;
    }
}

（4）最多能完成排序的块(769)

给定一个长度为 n 的整数数组 arr ，它表示在 [0, n - 1] 范围内的整数的排列。
我们将 arr 分割成若干 块 (即分区)，并对每个块单独排序。将它们连接起来后，使得连接的结果和按升序排序后的原数组相同。
返回数组能分成的最多块数量。

输入: arr = [4,3,2,1,0]
输出: 1
解释:
将数组分成2块或者更多块，都无法得到所需的结果。
例如，分成 [4, 3], [2, 1, 0] 的结果是 [3, 4, 0, 1, 2]，这不是有序的数组。

输入: arr = [1,0,2,3,4]
输出: 4
解释:
我们可以把它分成两块，例如 [1, 0], [2, 3, 4]。
然而，分成 [1, 0], [2], [3], [4] 可以得到最多的块数。
对每个块单独排序后，结果为 [0, 1], [2], [3], [4]

public class Solution {

    public static void main(String[] args) {
        int[] arr={1,0,2,3,4};
        Solution solution=new Solution();
        System.out.println(solution.maxChunksToSorted(arr));
    }

    public int maxChunksToSorted(int[] arr) {
        int n=arr.length;
        if (arr.length==1){
            return 1;
        }
        int maxCount=0;//可以分成的最大块数
        int preMax=0;//当前最大值
        for (int i=0;i<n;i++){
            preMax=Math.max(preMax,arr[i]);
            //如果当前最大值等于当前的i值
            if (preMax==i){
                maxCount++;//可以分块数+1
            }
        }
        return maxCount;
    }
}

2.栈和队列

（1）用栈实现队列(232)

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false
说明：

你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

public class MyQueue {

    Stack<Integer> stack1;
    Stack<Integer> stack2;

    public MyQueue() {
        stack1=new Stack<>();
        stack2=new Stack<>();
    }

    public void push(int x) {
        while (!stack2.isEmpty()){
            stack1.push(stack2.pop());
        }
        stack1.push(x);
    }

    public int pop() {
        if (stack2.isEmpty()){
            while (!stack1.isEmpty()){
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();
    }

    public int peek() {
        if (stack2.isEmpty()){
            while (!stack1.isEmpty()){
                stack2.push(stack1.pop());
            }
        }
        return stack2.peek();
    }

    public boolean empty() {
        if (stack1.empty()&& stack2.empty()){
            return true;
        }
        return false;
    }
}


public class QueueTest {

    public static void main(String[] args) {
        MyQueue queue=new MyQueue();
        queue.push(1);
        queue.push(2);
        queue.push(3);
        //System.out.println("pop():"+queue.pop());
        System.out.println("peak():"+queue.peek());
        System.out.println("empty():"+queue.empty());
        queue.push(4);
        System.out.println("====================");
        System.out.println("pop():"+queue.pop());
        System.out.println("peak():"+queue.peek());
        System.out.println("empty():"+queue.empty());
    }

}

（2）最小栈(155)

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。

public class MinStack {

    Stack<Integer> stack;//普通栈
    Stack<Integer> minStack;//返回最小值的栈

    public MinStack() {
        stack=new Stack<>();
        minStack=new Stack<>();
        minStack.push(Integer.MAX_VALUE);
    }

    public void push(int val) {
        stack.push(val);
        //最小值栈保存当前元素加进来后 栈中的最小值
        minStack.push(Math.min(minStack.peek(),val));
    }

    public void pop() {
        stack.pop();
        //当前元素出栈时 最小值栈对应的位置也要出栈
        minStack.pop();
    }

    public int top() {
        return stack.peek();
    }

    public int getMin() {
        return minStack.peek();
    }

}


public class MinStackTest {

    public static void main(String[] args) {
        MinStack stack=new MinStack();
        stack.push(-3);
        stack.push(1);
        stack.push(23);
        System.out.println(stack.getMin());
    }

}

（3）有效的括号(20)

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。
有效字符串需满足：
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

输入：s = "()"
输出：true

输入：s = "()[]{}"
输出：true

输入：s = "(]"
输出：false

public class Solution {

    public static void main(String[] args) {
        String s="()[]{}";
        Solution solution=new Solution();
        System.out.println(solution.isValid(s));
    }

    public boolean isValid(String s) {
        int n=s.length();
        //长度为奇数直接返回false
        if (n%2!=0){
            return false;
        }
        Stack<Character> stack=new Stack<>();
        Map<Character,Character> map=new HashMap<>();
        //将右括号和左括号分别以 key 和 value 存储
        map.put(')','(');
        map.put('}','{');
        map.put(']','[');
        //遍历字符串匹配括号
        for (int i=0;i<n;i++){
            char ch=s.charAt(i);
            if (map.containsKey(ch)){//如果ch是map集合里的key 也就是右括号
                //先判断stack是否为空或者栈顶元素是否与ch匹配
                if (stack.isEmpty()||stack.peek()!=map.get(ch)){
                    return false;
                }
                //如果匹配
                stack.pop();//弹出栈顶括号
            }else {//如果ch是左括号
                stack.push(ch);
            }
        }
        return stack.isEmpty();
    }
}

3.单调栈

（1）每日温度

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]

输入: temperatures = [30,60,90]
输出: [1,1,0]

public class Solution {

    public static void main(String[] args) {
        int[] arr={73,74,75,71,69,72,76,73};
        Solution solution=new Solution();
        int[] tem = solution.dailyTemperatures(arr);
        for (int i=0;i< tem.length;i++){
            System.out.print(tem[i]+" ");
        }
    }

    public int[] dailyTemperatures(int[] temperatures) {
        int n = temperatures.length;
        if (n==1){
            return new int[1];
        }
        int[] arr=new int[n];
        Stack<Integer> stack=new Stack<>();
        for (int i=0;i<n;i++){
            //当栈不为空并且栈顶温度小于当前温度时
            while (!stack.isEmpty()&&temperatures[i]>temperatures[stack.peek()]){
                arr[stack.peek()]=i-stack.pop();
            }
            //当上边两个条件不全满足时 将当前元素的下标入栈
            stack.push(i);
        }

        return arr;
    }
}

4.优先队列

（1）合并K个升序链表(23)

给你一个链表数组，每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中，返回合并后的链表。

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

输入：lists = []
输出：[]

输入：lists = [[]]
输出：[]

//顺序遍历合并每一个链表
public class Solution {

    public ListNode mergeKLists(ListNode[] lists) {
        ListNode list=null;//需要返回的链表
        //遍历每一个链表 然后与list合并
        for (int i=0;i< lists.length;i++){
            list=mergeTwoLists(lists[i],list);
        }
        return list;
    }

    private ListNode mergeTwoLists(ListNode a,ListNode b){
        if (a==null||b==null){
            return a!=null?a:b;
        }
        ListNode head=new ListNode(0);//设置一个头节点 返回的时候返回他的next节点
        ListNode tail=head;//记录下一个插入位置的前一个位置
        ListNode preA=a;//a链表的当前节点
        ListNode preB=b;//b链表的当前节点
        while (preA!=null&&preB!=null){
            if (preA.val<preB.val){
                tail.next=preA;
                preA=preA.next;
            }else {
                tail.next=preB;
                preB=preB.next;
            }
            tail=tail.next;
        }
        tail.next=preA!=null?preA:preB;
        return head.next;
    }
}


//采用分治合并
public class Solution {

    public ListNode mergeKLists(ListNode[] lists) {
        return merge(lists,0,lists.length-1);
    }

    private ListNode merge(ListNode[] lists,int left,int right){
        if (left==right){
            return lists[left];
        }
        if (left>right){
            return null;
        }
        int mid=(left+right)>>1;//因为lists.length<500 所以这里不用担心越界 可以使用left+right
        return mergeTwoLists(merge(lists, left, mid),merge(lists, mid+1, right));
    }

    private ListNode mergeTwoLists(ListNode a,ListNode b){
        if (a==null||b==null){
            return a!=null?a:b;
        }
        ListNode head=new ListNode(0);//设置一个头节点 返回的时候返回他的next节点
        ListNode tail=head;//记录下一个插入位置的前一个位置
        ListNode preA=a;//a链表的当前节点
        ListNode preB=b;//b链表的当前节点
        while (preA!=null&&preB!=null){
            if (preA.val<preB.val){
                tail.next=preA;
                preA=preA.next;
            }else {
                tail.next=preB;
                preB=preB.next;
            }
            tail=tail.next;
        }
        tail.next=preA!=null?preA:preB;
        return head.next;
    }
} 

5.双端队列

（1）滑动窗口最大值(239)

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

输入：nums = [1], k = 1
输出：[1]

//优先队列
public class Solution {

    public static void main(String[] args) {
        int[] arr={1,3,-1,-3,5,3,6,7};
        int k=3;
        Solution solution=new Solution();
        int[] ints = solution.maxSlidingWindow(arr, k);
        for (int i:ints) {
            System.out.print(i+" ");
        }
    }

    public int[] maxSlidingWindow(int[] nums, int k) {
        int n= nums.length;
        int[] res=new int[n-k+1];
        //定义一个大根堆
        PriorityQueue<int[]> heap=new PriorityQueue<>(new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                if (o1[0]!=o2[0]){//如果元素值不相等 按照元素值降序排序
                    return o2[0]-o1[0];
                }
                //如果元素值相等 按照索引值降序排序
                return o2[1]-o1[1];
            }
        });
        //将数组前k个元素加入大根堆
        for (int i=0;i<k;i++){
            heap.add(new int[]{nums[i],i});
        }
        res[0]=heap.peek()[0];
        //开始滑动窗口
        for (int i=k;i<n;i++){
            heap.add(new int[]{nums[i],i});//当前元素加入大根堆
            //如果此时最大值不在窗口内 就将堆顶元素移除 直到堆顶元素最大值在当前窗口内
            //此时堆顶元素就是当前窗口内的最大值
            while (heap.peek()[1]<=i-k){
                heap.poll();//弹出堆顶元素
            }
            res[i-k+1]=heap.peek()[0];
        }
        return res;
    }
}

6.哈希表

哈希表又称为散列表，使用O(n)的空间复杂度存储数据，通过hash函数映射位置，从而实现近似O(1)的时间
复杂度的插入、删除、查找等操作

（1）两数之和(1)

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。

//暴力遍历
class Solution {

    public static void main(String[] args) {
        int[] arr={2,7,11,15};
        int k=9;
        Solution solution=new Solution();
        int[] ints = solution.twoSum(arr, k);
        for (int i:ints) {
            System.out.print(i+" ");
        }
    }
    
    public int[] twoSum(int[] nums, int target) {
        int n= nums.length;
        for (int i=0;i<n-1;i++){
            for (int j=i+1;j<n;j++){
                if (nums[j]==target-nums[i]){
                    return new int[]{i,j};
                }
            }
        }
        return new int[0];
    }
}


//使用hash表
public class Solution {

    public static void main(String[] args) {
        int[] arr={2,7,11,15};
        int k=9;
        Solution solution=new Solution();
        int[] ints = solution.twoSum(arr, k);
        for (int i:ints) {
            System.out.print(i+" ");
        }
    }

    public int[] twoSum(int[] nums, int target) {
        int n= nums.length;
        Map<Integer,Integer> map=new HashMap<>();
        for (int i=0;i<n;i++){
            //如果map里存在一个key使它和当前值相加等于target 直接返回他们的下标
            if (map.containsKey(target-nums[i])){
                return new int[]{map.get(target-nums[i]),i};
            }
            map.put(nums[i],i);
        }
        return new int[0];
    }
}

（2）最长连续序列(128)

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

输入：nums = [0,3,7,2,5,8,4,6,0,1]
输出：9

public class Solution {

    public static void main(String[] args) {
        int[] arr={100,4,200,1,3,2};
        Solution solution=new Solution();
        System.out.println(solution.longestConsecutive(arr));
    }

    public int longestConsecutive(int[] nums) {
        int n= nums.length;
        if (n==0){
            return 0;
        } else if (n==1) {
            return 1;
        }
        Set<Integer> set=new HashSet<>();
        int longestLen=0;//最长序列长度
        //将数组中元素加入set集合中 并去重
        for (int i=0;i<n;i++){
            set.add(nums[i]);
        }
        //遍历数组中每一个元素
        for (int i=0;i<n;i++){
            //当一个元素在数组中不存在前驱元素时 从这个元素出发才可以得到当前最长序列
            //如果存在前驱元素 那么从前驱元素开始 得到的序列长度一定大于从当前这个元素开始的序列长度
            if (!set.contains(nums[i]-1)){
                int curLen=1;//当前长度
                int curNum=nums[i];//当前元素
                //当当前元素存在后继元素时 当前长度+1
                while (set.contains(curNum+1)){
                    curLen++;
                    curNum++;
                }
                longestLen=Math.max(longestLen,curLen);
            }
        }
        return longestLen;
    }
}

（3）直线上最多的点数

给你一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。

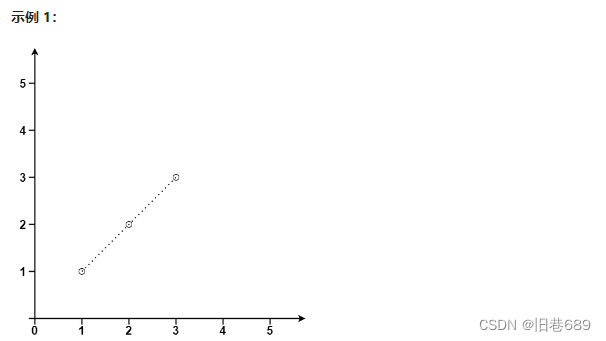
输入：points = [[1,1],[2,2],[3,3]]
输出：3

public class Solution {

    public static void main(String[] args) {
        int[][] arr={{1,1},{3,2},{5,3},{4,1},{2,3},{1,4}};
        Solution solution=new Solution();
        System.out.println(solution.maxPoints(arr));
    }

    public int maxPoints(int[][] points) {
        int n=points.length;
        if (n<=2){
            return n;
        }
        int maxPoint=0;//最多有多少个点在同一条直线上
        for (int i=0;i<n;i++){
            //当共线点的数量 > n/2时 或者 共线点的数量 >= 当前点i之后所剩的点的数量时 就直接退出循环
            if (maxPoint>=n-i||maxPoint>n/2){
                break;
            }
            //用map集合来存储每个不同直线上共线点的个数
            Map<Integer,Integer> map=new HashMap<>();
            for (int j=i+1;j<n;j++){
                int x=points[j][0]-points[i][0];
                int y=points[j][1]-points[i][1];
                //当x=0或者y=0时 将不为0的一方设置为1
                if (x==0){
                    y=1;
                } else if (y==0) {
                    x=1;
                }else {
                    //假设y始终为正数
                    if (y<0){
                        x=-x;
                        y=-y;
                    }
                    //求x和y的最大公倍数
                    int gcdXY=gcd(Math.abs(x),Math.abs(y));
                    //化简x和y
                    x/=gcdXY;
                    y/=gcdXY;
                }
                //将x和y用一个正数表示 作为集合的key
                int key=y+20001*x;
                if (map.containsKey(key)){//当集合中存在key时 点数+1
                    map.put(key,map.get(key)+1);
                }else {//集合中不存在key时 将这个key加入集合
                    map.put(key,1);
                }
            }
            int preMax=0;//当前i所在的最大点数
            //遍历当前的map集合 求出当前的最大值
            for (Map.Entry<Integer,Integer> entry: map.entrySet()){
                preMax=Math.max(preMax, entry.getValue()+1);
            }
            //将每一次的当前最大值与最大值做比较 求总的最大值
            maxPoint=Math.max(preMax,maxPoint);
        }
        return maxPoint;
    }

    private int gcd(int x,int y){
        return y!=0?gcd(y,x%y):x;
    }
}

7.前缀和与积分图

（1）区域和检索 - 数组不可变(303)

给定一个整数数组 nums，处理以下类型的多个查询:
计算索引 left 和 right （包含 left 和 right）之间的 nums 元素的 和 ，其中 left <= right
实现 NumArray 类：
NumArray(int[] nums) 使用数组 nums 初始化对象
int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + … + nums[right] )

//暴力
public class NumArray {

    int[] arr;

    public NumArray(int[] nums) {
        this.arr=nums;
    }

    public int sumRange(int left, int right) {
        int sum=0;
        for (int i=left;i<=right;i++){
            sum+=arr[i];
        }
        return sum;
    }

}


//前缀和
public class NumArray {

    int[] arr;//前缀和数组

    public NumArray(int[] nums) {
        int n=nums.length;
        arr=new int[n+1];//前缀和数组的arr[0]=0 这样可以避免i=0的特殊判断
        for (int i=0;i<n;i++){
            arr[i+1]=arr[i]+nums[i];
        }
    }

    public int sumRange(int left, int right) {
        //left~right这个区间元素的和是 0~right的前缀和减去0~left-1的前缀和的值
        return arr[right+1]-arr[left];
    }

}

（2）二维区域和检索 - 矩阵不可变(304)

给定一个二维矩阵 matrix，以下类型的多个请求：
计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。
实现 NumMatrix 类：
NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

//使用一维前缀和
public class NumMatrix {

    int arr[][];

    public NumMatrix(int[][] matrix) {
        int m= matrix.length;//行
        int n=matrix[0].length;//列
        arr=new int[m][n+1];
        for (int i=0;i<m;i++){
            //计算出每一行的前缀和
            for (int j=0;j<n;j++){
                arr[i][j+1]=arr[i][j]+matrix[i][j];
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        int sum=0;
        for (int i=row1;i<=row2;i++){
            sum+=arr[i][col2+1]-arr[i][col1];
        }
        return sum;
    }

}


//使用二维前缀和
public class NumMatrix {

    int arr[][];

    public NumMatrix(int[][] matrix) {
        int m= matrix.length;//行
        int n=matrix[0].length;//列
        arr=new int[m+1][n+1];
        //计算出第一行的所有列的前缀和
        for (int i=0;i<m;i++){
            for (int j=0;j<n;j++){
                arr[i+1][j+1]=arr[i][j+1]+arr[i+1][j]-arr[i][j]+matrix[i][j];
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        return arr[row2+1][col2+1]-arr[row1][col2+1]-arr[row2+1][col1]+arr[row1][col1];
    }

}

（3）和为 K 的子数组(560)

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的连续子数组的个数 。

输入：nums = [1,1,1], k = 2
输出：2

输入：nums = [1,2,3], k = 3
输出：2

//暴力枚举
public class Solution {

    public static void main(String[] args) {
        int[] arr={1,2,3};
        int k=3;
        Solution solution=new Solution();
        System.out.println(solution.subarraySum(arr,k));
    }

    public int subarraySum(int[] nums, int k) {
        int n= nums.length;
        int count=0;//连续子数组的个数
        //依次遍历每个元素 分别以每个元素结尾向前寻找 看能否找到连续子数组的和为k
        for (int i=0;i<n;i++){
            int sum=0;//连续子数组的和
            for (int j=i;j>=0;j--){
                sum+=nums[j];
                if (sum==k){
                    count++;
                }
            }
        }
        return count;
    }
}


//前缀和+哈希表优化
public class Solution {

    public static void main(String[] args) {
        int[] arr={1,2,3};
        int k=3;
        Solution solution=new Solution();
        System.out.println(solution.subarraySum(arr,k));
    }

    public int subarraySum(int[] nums, int k) {
        int n= nums.length;
        int count=0;//连续子数组的个数
        int pre=0;//前缀和
        Map<Integer,Integer> map=new HashMap<>();
        map.put(pre,1);
        for (int i=0;i<n;i++){
            pre+=nums[i];
            if (map.containsKey(pre-k)){
                count+=map.get(pre-k);
            }
            map.put(pre,map.getOrDefault(pre,0)+1);
        }
        return count;
    }
}

8.练习

（1）重塑矩阵(566)

在 MATLAB 中，有一个非常有用的函数 reshape ，它可以将一个 m x n 矩阵重塑为另一个大小不同（r x c）的新矩阵，但保留其原始数据。

给你一个由二维数组 mat 表示的 m x n 矩阵，以及两个正整数 r 和 c ，分别表示想要的重构的矩阵的行数和列数。

重构后的矩阵需要将原始矩阵的所有元素以相同的 行遍历顺序 填充。

如果具有给定参数的 reshape 操作是可行且合理的，则输出新的重塑矩阵；否则，输出原始矩阵。

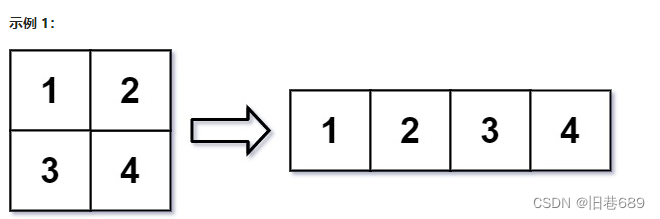
输入：mat = [[1,2],[3,4]], r = 1, c = 4
输出：[[1,2,3,4]]

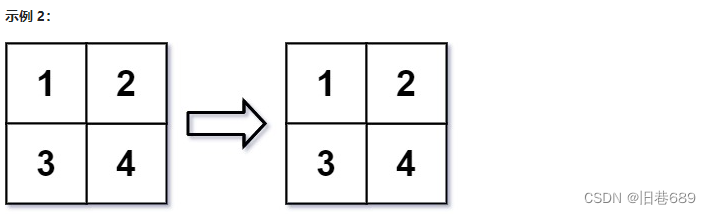
输入：mat = [[1,2],[3,4]], r = 2, c = 4
输出：[[1,2],[3,4]]

public class Solution {

    public static void main(String[] args) {
        int[][] arr={{1,2},{3,4}};
        int r=1;
        int c=4;
        Solution solution=new Solution();
        int[][] ints = solution.matrixReshape(arr, r, c);
        System.out.println("行:"+ints.length+"   "+"列:"+ints[0].length);
    }

    public int[][] matrixReshape(int[][] mat, int r, int c) {
        int m= mat.length;
        int n=mat[0].length;
        if (r*c!=m*n){
            return mat;
        }
        int[][] arr=new int[r][c];
        Queue<Integer> queue=new LinkedList<>();
        //将数组元素入队列
        for (int i=0;i<m;i++){
            for (int j=0;j<n;j++){
                queue.add(mat[i][j]);
            }
        }
        //将队列的元素插入新的数组
        for (int i=0;i<r;i++){
            for (int j=0;j<c;j++){
                arr[i][j]=queue.poll();
            }
        }
        return arr;
    }
}

（2）用队列实现栈(225)

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

public class MyStack {

    Queue<Integer> queue;
    Queue<Integer> auxQueue;//辅助栈

    public MyStack() {
        queue=new LinkedList<>();
        auxQueue=new LinkedList<>();
    }

    public void push(int x) {
        //首先将queue里剩余的元素弹入auxQueue中 为了保证元素顺序
        while (!queue.isEmpty()){
            auxQueue.add(queue.poll());
        }
        //将auxQueue中元素按照顺序弹入queue中
        while (!auxQueue.isEmpty()){
            queue.add(auxQueue.poll());
        }
        queue.add(x);
    }

    public int pop() {
        //首先将queue里剩余的元素弹入auxQueue中 为了保证元素顺序
        while (!queue.isEmpty()){
            auxQueue.add(queue.poll());
        }
        //在每一次操作前 先将auxQueue中的元素弹入queue中
        while (!auxQueue.isEmpty()){
            queue.add(auxQueue.poll());
        }
        while (queue.size()>1){
            auxQueue.add(queue.poll());
        }
        return queue.poll();
    }

    public int top() {
        //首先将queue里剩余的元素弹入auxQueue中 为了保证元素顺序
        while (!queue.isEmpty()){
            auxQueue.add(queue.poll());
        }
        //在每一次操作前 先将auxQueue中的元素弹入queue中
        while (!auxQueue.isEmpty()){
            queue.add(auxQueue.poll());
        }
        while (queue.size()>1){
            auxQueue.add(queue.poll());
        }
        return queue.peek();
    }

    public boolean empty() {
        while (queue.isEmpty()&&auxQueue.isEmpty()){
            return true;
        }
        return false;
    }
}

（3）下一个更大元素 II(503)

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。

数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]

//小根堆+循环数组
public class Solution {

    public static void main(String[] args) {
        int[] arr={1,2,1};
        Solution solution=new Solution();
        int[] ints = solution.nextGreaterElements(arr);
        for (int i:ints){
            System.out.print(i+" ");
        }
    }

    public int[] nextGreaterElements(int[] nums) {
        int n= nums.length;
        if (n==1){
            return new int[]{-1};
        }
        int[] arr=new int[n];
        //先将数组中所有位置初始化为-1
        Arrays.fill(arr,-1);
        PriorityQueue<int[]> heap=new PriorityQueue<>(new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                if (o1[0]==o2[0]){
                    return o1[1]-o2[1];
                }
                return o1[0]-o2[0];
            }
        });
        for (int i=0;i<n*2-1;i++){
            //当小根堆不为空并且堆顶元素小于当前元素时 堆顶元素对应位置放当前元素
            while (!heap.isEmpty()&&heap.peek()[0]<nums[i%n]){
                arr[heap.poll()[1]]=nums[i%n];
            }
            //当前元素入堆
            heap.add(new int[]{nums[i%n],i%n});
        }
        return arr;
    }
}


//单调栈+循环数组
public class Solution {

    public static void main(String[] args) {
        int[] arr={1,2,1};
        Solution solution=new Solution();
        int[] ints = solution.nextGreaterElements(arr);
        for (int i:ints){
            System.out.print(i+" ");
        }
    }

    public int[] nextGreaterElements(int[] nums) {
        int n= nums.length;
        if (n==1){
            return new int[]{-1};
        }
        int[] arr=new int[n];
        //先将数组中所有位置初始化为-1
        Arrays.fill(arr,-1);
        //单调栈中保存数组元素下标
        Deque<Integer> stack=new LinkedList<>();
        for (int i=0;i<n*2-1;i++){
            //当栈不为空并且当前元素大于栈顶下标所对应的元素时 将栈顶元素对应位置赋值为当前元素
            while (!stack.isEmpty()&&nums[stack.peek()]<nums[i%n]){
                arr[stack.poll()]=nums[i%n];
            }
            //当前元素下标入栈
            stack.push(i%n);
        }
        return arr;
    }
}

（4）存在重复元素(217)

给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ，返回 true ；如果数组中每个元素互不相同，返回 false 。

输入：nums = [1,2,3,1]
输出：true

输入：nums = [1,2,3,4]
输出：false

输入：nums = [1,1,1,3,3,4,3,2,4,2]
输出：true

//排序
public class Solution {

    public static void main(String[] args) {
        int[] arr={1,2,1};
        Solution solution=new Solution();
        System.out.println(solution.containsDuplicate(arr));
    }

    public boolean containsDuplicate(int[] nums) {
        int n=nums.length;
        if (n==1){
            return false;
        }
        Arrays.sort(nums);
        for (int i=0;i<n-1;i++){
            if (nums[i]==nums[i+1]){
                return true;
            }
        }
        return false;
    }
}


//集合
public class Solution {

    public static void main(String[] args) {
        int[] arr={1,2,1};
        Solution solution=new Solution();
        System.out.println(solution.containsDuplicate(arr));
    }

    public boolean containsDuplicate(int[] nums) {
        int n=nums.length;
        if (n==1){
            return false;
        }
        Set<Integer> set=new HashSet<>();
        for (int i=0;i<n;i++){
            //当集合中存在某个值时 证明这个值算上当前值至少出现了两次 直接返回true
            if (set.contains(nums[i])){
                return true;
            }
            set.add(nums[i]);
        }
        return false;
    }
}

（5）数组的度

给定一个非空且只包含非负数的整数数组 nums，数组的 度 的定义是指数组里任一元素出现频数的最大值。

你的任务是在 nums 中找到与 nums 拥有相同大小的度的最短连续子数组，返回其长度。

输入：nums = [1,2,2,3,1]
输出：2
解释：
输入数组的度是 2 ，因为元素 1 和 2 的出现频数最大，均为 2 。
连续子数组里面拥有相同度的有如下所示：
[1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2]
最短连续子数组 [2, 2] 的长度为 2 ，所以返回 2 。

输入：nums = [1,2,2,3,1,4,2]
输出：6
解释：
数组的度是 3 ，因为元素 2 重复出现 3 次。
所以 [2,2,3,1,4,2] 是最短子数组，因此返回 6 。

//哈希表
public class Solution {

    public static void main(String[] args) {
        int[] arr={1,2,2,3,1};
        Solution solution=new Solution();
        System.out.println(solution.findShortestSubArray(arr));
    }

    public int findShortestSubArray(int[] nums) {
        int n= nums.length;
        if (n==1){
            return 1;
        }
        int maxCount=0;//出现最大的频数
        int minLen=0;//出现频数最多且子数组长度最短的长度
        //哈希表 用来存储元素 和 其出现的次数以及第一次出现和最后一次出现的位置
        Map<Integer,int[]> map=new HashMap<>();
        for (int i=0;i<n;i++){
            if (map.containsKey(nums[i])){
                //更新出现的次数已经最后一次出现的位置
                map.get(nums[i])[0]++;
                map.get(nums[i])[2]=i;
            }else {
                map.put(nums[i],new int[]{1,i,i});
            }
        }
        //依次获取每一个value 比较它们的次数以及对应的子数组的长度 得到答案
        for (Map.Entry<Integer,int[]> entry:map.entrySet()){
            int[] arr= entry.getValue();
            if (maxCount<arr[0]){
                maxCount=arr[0];//令maxCount=当前频数
                minLen=arr[2]-arr[1]+1;//更改当前最短子数组长度
            } else if (maxCount==arr[0]) {
                minLen=Math.min(minLen,arr[2]-arr[1]+1);
            }
        }
        return minLen;
    }
}

（6）最长和谐子序列(594)

和谐数组是指一个数组里元素的最大值和最小值之间的差别 正好是 1 。

现在，给你一个整数数组 nums ，请你在所有可能的子序列中找到最长的和谐子序列的长度。

数组的子序列是一个由数组派生出来的序列，它可以通过删除一些元素或不删除元素、且不改变其余元素的顺序而得到。

输入：nums = [1,3,2,2,5,2,3,7]
输出：5
解释：最长的和谐子序列是 [3,2,2,2,3]

输入：nums = [1,2,3,4]
输出：2

输入：nums = [1,1,1,1]
输出：0

//排序
public class Solution {

    public static void main(String[] args) {
        int[] arr={1,2,3,4};
        Solution solution=new Solution();
        System.out.println(solution.findLHS(arr));
    }

    public int findLHS(int[] nums) {
        int n= nums.length;
        if (n<2){
            return 0;
        }
        int maxLen=0;//最长和谐子序列的长度
        Arrays.sort(nums);
        for (int i=0;i<n-1;i++){
            int j=i;
            int preMin=nums[i];//当前和谐子序列最小值
            //当当前子序列满足和谐子序列时
            while (j<(n-1)&&(preMin+1)>=nums[j+1]){
                j++;
            }
            //当当前最小值不等于最大值时 才成立
            if (preMin!=nums[j]){
                maxLen=Math.max(maxLen,j-i+1);
            }
        }
        return maxLen;
    }

}


//哈希表
public class Solution {

    public static void main(String[] args) {
        int[] arr={1,2,3,4};
        Solution solution=new Solution();
        System.out.println(solution.findLHS(arr));
    }

    public int findLHS(int[] nums) {
        int n= nums.length;
        if (n<2){
            return 0;
        }
        int maxLen=0;//最长和谐子序列的长度
        Map<Integer,Integer> map=new HashMap<>();
        //遍历数组 得到每个元素出现的次数
        for (int i=0;i<n;i++){
            if (map.containsKey(nums[i])){
                map.put(nums[i],map.get(nums[i])+1);
            }else {
                map.put(nums[i],1);
            }
        }
        //遍历map 对每一个key值 如果找到key+1也在map里 那么它们对应的和谐子序列长度就是它们的value值相加
        for (int key:map.keySet()){
            if (map.containsKey(key+1)){
                maxLen=Math.max(maxLen,map.get(key)+map.get(key+1));
            }
        }
        return maxLen;
    }

}

（7）寻找重复数(287)

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。

你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

输入：nums = [1,3,4,2,2]
输出：2

输入：nums = [3,1,3,4,2]
输出：3

public class Solution {

    public static void main(String[] args) {
        int[] arr={3,1,3,4,2};
        Solution solution=new Solution();
        System.out.println(solution.findDuplicate(arr));
    }

    public int findDuplicate(int[] nums) {
        int n= nums.length;
        int repeatNum=0;//重复的整数
        int left=1;
        int right=n-1;
        while (left<=right){
            int mid=(left+right)>>1;
            int count=0;//计数 来判断重复的数出现在哪
            for (int i=0;i<n;i++){
                if (nums[i]<=mid){
                    count++;
                }
            }
            if (count<=mid){
                left=mid+1;
            }else {
                right=mid-1;
                repeatNum=mid;
            }
        }
        return repeatNum;
    }

}

（8）优势洗牌(870)

给定两个大小相等的数组 nums1 和 nums2，nums1 相对于 nums2 的优势可以用满足 nums1[i] > nums2[i] 的索引 i 的数目来描述。
返回 nums1 的任意排列，使其相对于 nums2 的优势最大化。

输入：nums1 = [2,7,11,15], nums2 = [1,10,4,11]
输出：[2,11,7,15]

输入：nums1 = [12,24,8,32], nums2 = [13,25,32,11]
输出：[24,32,8,12]

    public int[] advantageCount(int[] nums1, int[] nums2) {
        int n= nums1.length;
        int[] arr=new int[n];
        Integer[] a=new Integer[n];
        Integer[] b=new Integer[n];
        int left=0;//数组当前左边界
        int right=n-1;//数组当前有边界
        for (int i=0;i<n;i++){
            a[i]=i;
            b[i]=i;
        }
        //a b 分别来存储 nums1 nums2 排序后的下标值
        Arrays.sort(a,(i,j)->nums1[i]-nums1[j]);
        Arrays.sort(b,(i,j)->nums2[i]-nums2[j]);
        for (int i=0;i<n;i++){
            //当nums1的当前最小值大于nums2的当前最小值时
            if (nums1[a[i]]>nums2[b[left]]){
                arr[b[left]]=nums1[a[i]];
                left++;
            }else {
                arr[b[right]]=nums1[a[i]];
                right--;
            }
        }
        return arr;
    }