当前位置：首页 > news >正文

【算法】二叉树

news 来源：原创 2024/11/15 6:17:06

❤️ Author：老九
☕️ 个人博客：老九的CSDN博客
🙏 个人名言：不可控之事乐观面对
😍 系列专栏：

文章目录

二叉树
- 数组转化为二叉树
- 二叉树转化为二叉链表
二叉树的遍历
排序二叉树BST（二叉搜索树）

二叉树

当一颗二叉树有n个结点时，就会有n-1个线条
完全二叉树：除最后一层的右不满以外，其他层都是满的
如果一个完全二叉树的结点从上到下，从左到右从0开始编号，一个结点和两个子结点的编号为，n，2n+1，2n+2，一个结点父结点是：Math.floor((m-1)/2)

  {
    val : 3,
    left : {
      val : 1,
      left : null,
      right : null,
    },
    right : {
      val : 5,
      left : null,
      right : null
    }
  }

数组转化为二叉树

<script>
  //将存储于array中的根节 点在rootPos位置的二叉树转换为二叉链表形式
  function arrayToTree(array, rootPos = 0) {
    if (array[rootPos] === null) {
      return null
    }
    var root = {
      var: array[rootPos],
      left: null,
      right: null,
    }
    root.left = arrayToTree(array, rootPos * 2 + 1)
    root.right = arrayToTree(array, rootPos * 2 + 2)

    return root
  }
</script>

但是上面的做法会有null，比较占用空间

<script>
  function condensedArrayToTree(ary) {
    if (ary.length == 0) {
      return null
    }
    var root = {
      val: ary[0],
      left: null,
      right: null,
    }
    var nodes = [root]
    for (var i = 1; i < ary.length; i++) {
      var currNode = nodes.shift()
      if (ary[i] != null) {
        var node = {
          val: ary[i],
          left: null,
          right: null
        }
        currNode.left = node
        nodes.push(node)
      }
      i++
      if (ary[i] != null) {
        var node = {
          val: ary[i],
          left: null,
          right: null
        }
        currNode.right = node
        nodes.push(node)
      }
    }
    return root
  }
  condensedArrayToTree([1,null,2,3,null,null,4,null,5])
</script>

二叉树转化为二叉链表

<script>
  function treeToArray(root, pos = 0, result = []) {
    if (root == null) {
      return
    }
    result[pos] = root.val

    treeToArray(root.left, pos * 2 + 1, result)
    treeToArray(root.right, pos * 2 + 2, result)

    return result
  }
</script>

加强版树转数组

<script>
  function treeToCondensedArray(root){
    var ary = []
    if(!root){
      return ary
    }
    var nodes = [root]
    while(nodes.length){
      var node = nodes.shift()
      if(node){
        ary.push(node.val)
        nodes.push(node.left)
        nodes.push(node.right)
      }else{
        ary.push(node)
      }
    }
    return ary
  }
</script>

二叉树的遍历

按层遍历：从上到下，从左到右遍历每一层的结点
先序遍历，先遍历根节点，再遍历左子树，最后遍历右子树，对子树的遍历依然遵循此规则
还有中序遍历，后序遍历
先序遍历画轮廓，10628439578
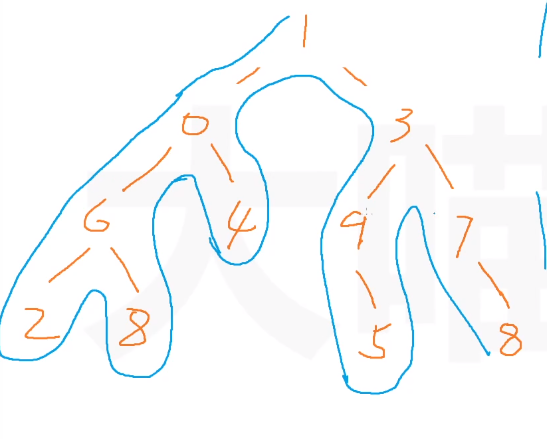
中序遍历也是画轮廓，先把叶子节点补上，然后数第二次碰到的结点，26804195378
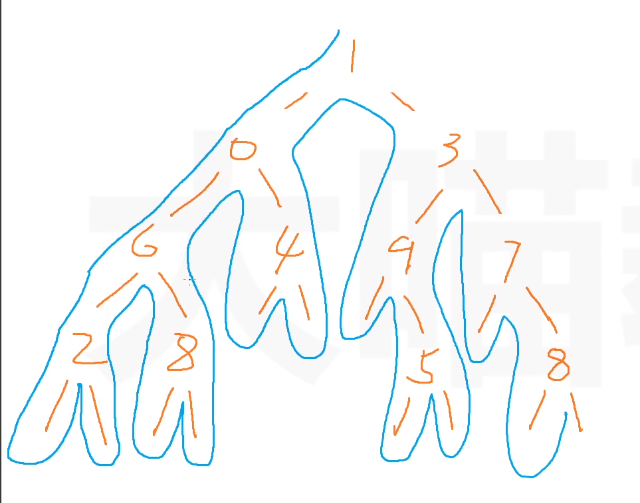
后序遍历是第三次碰到每个结点的时候计数，画法和中序遍历画法一样，28640598731

<script>

  function preOrderTraverse(root) {
    if (root) {
      console.log(root.val)
      preOrderTraverse(root.left)
      preOrderTraverse(root.right)
    }
  }
  function inOrderTraverse(root){
    if(root){
      inOrderTraverse(root.left)
      console.log(root.val)
      inOrderTraverse(root.right)
    }
  }
  function postOrderTraverse(root){
    if(root){
      postOrderTraverse(root.left)
      postOrderTraverse(root.right)
      console.log(root.val)
    }
  }
  condensedArrayToTree([1,0,3,6,4,9,7,2,8,,,,5,,8])
  //高级版本
  function preOrderTraverseH(root, action) {
    if (root) {
      action(root.val)
      preOrderTraverse(root.left, action)
      preOrderTraverse(root.right, action)
    }
  }

  </script>

排序二叉树BST（二叉搜索树）

一颗二叉树中的每个结点左子树中的结点都比它根节点小，每个结点的右子树中的结点比它根节点大或等于
排序二叉树的中序遍历结果是有序的
时间复杂度最差是n的平方，平均情况是n*logn
空间复杂度是构建出来的二叉树占用的空间，为n

<script>
  //通过val构建一个结点，并将结点插入到排序二叉树bst中的正确位置上，返回处理完成后的树的根节点
  function insertIntoBST(bst, val) {
    let node = {
      val: val,
      left: null,
      right: null
    }
    if (!bst) {
      return node
    }
    if (val < bst.val) {
      bst.left = insertIntoBST(bst.left, val)
    } else {
      bst.right = insertIntoBST(bst.right, val)
    }
    return bst
  }
  function inOrderTraverse(root, action) {
    if (root) {
      inOrderTraverse(root.left, action)
      action(root.val)
      inOrderTraverse(root.right, action)
    }
  }
  //利用二叉树来排序
  //构建一颗空的排序二叉树，将数组ary中的元素都插入这颗二叉树
  //完成后，中序遍历二叉树即可得到有序结果
  function bstSort(ary) {
    // var tree = null
    // for (var i = 0; i < ary.length; i++) {
    //   tree = insertIntoBST(tree, ary[i])
    // }
    var tree = ary.reduce((tree,it) => {
      return insertIntoBST(tree,it)
    },null)
    i = 0
    inOrderTraverse(tree, val => {
      ary[i] = val
      i++
    })
    return ary
  }
</script>