[LeetCode周赛复盘] 第 328 场周赛20230115

一、本周周赛总结

• 这场质量不错。
• T1 模拟。
• T2 二维前缀和/二维树状数组。
• T3 双指针/滑窗。
• T4 树形DP/换根DP。
  

二、 [Easy] 6291. 数组元素和与数字和的绝对差

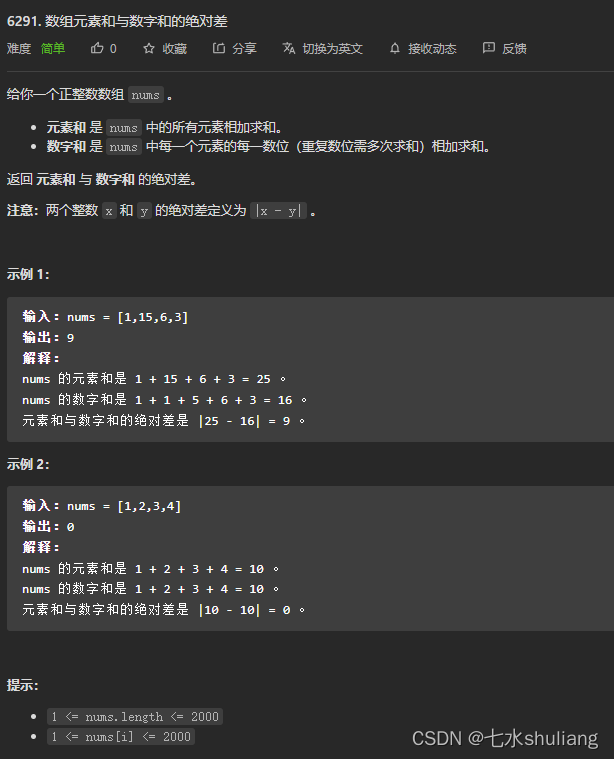
链接: 6291. 数组元素和与数字和的绝对差

1. 题目描述

2. 思路分析

按题意模拟即可。

3. 代码实现

class Solution:
    def differenceOfSum(self, nums: List[int]) -> int:        
        a = sum(nums)
        b = 0
        for x in nums:
            for i in str(x):
                b += int(i)
        return abs(a-b)

三、[Medium] 6292. 子矩阵元素加 1

链接: 6292. 子矩阵元素加 1

1. 题目描述

2. 思路分析

这题不会差分吃大亏，套了个一维树状数组TLE。

• 最后快结束了换一维差分能过。
• 正确应该是二维最快。
• 二维树状数组也可以过。

3. 代码实现

class Diff2D:
    """二维差分模板"""
    def __init__(self,g):
        self.m,self.n = len(g),len(g[0])
        # self.mat = [[0+]]+[[0]+r[:] for r in g]
        self.diff = [[0]*(self.n+1) for _ in range(self.m+1)]
    def add(self,x1,y1,x2,y2,v):
        x2 += 1
        y2 += 1
        self.diff[x1][y1] += v
        self.diff[x2][y1] -= v
        self.diff[x1][y2] -= v
        self.diff[x2][y2] += v
    def update(self):
        mat = [[0]*(self.n+1) for _ in range(self.m+1)]
        d = self.diff
        for i,row in enumerate(d[:-1]):
            for j,v in enumerate(row[:-1]):
                mat[i+1][j+1] = v - mat[i][j] + mat[i+1][j] + mat[i][j+1] 
        return [r[1:] for r in mat[1:]]

class Solution:
    def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:
        grid = [[0] * n for _ in range(n)]
        g = Diff2D(grid)
        for x1, y1, x2, y2 in queries:
            g.add(x1, y1, x2, y2 , 1)
        
        return g.update()

四、[Medium] 6293. 统计好子数组的数目

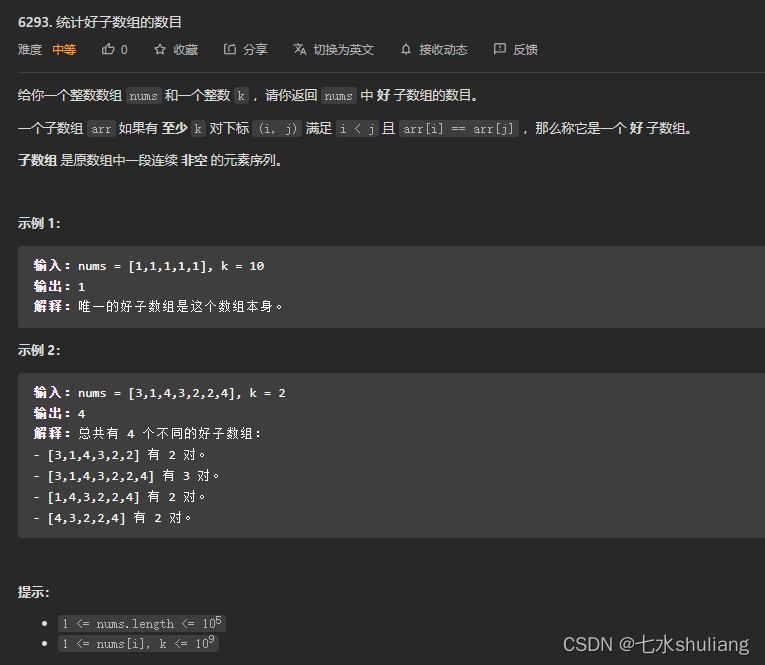
链接: 6293. 统计好子数组的数目

1. 题目描述

2. 思路分析

• 滑窗/双指针。
• 正难则反，显然坏子数组用滑窗更容易计算。
• 长度为n的数组，子段共n*(n+1)//2个，不断减去坏子数组的个数即可。

3. 代码实现

class Solution:
    def countGood(self, nums: List[int], k: int) -> int:
        n = len(nums)
        ans = n*(n+1)//2
        q = deque()
        c = Counter()
        p = 0
        for v in nums:
            q.append(v)
            c[v] += 1
            p += c[v]-1
            while p >= k:
                l = q.popleft()
                c[l] -= 1
                p -= c[l]
            ans -= len(q)
        return ans

五、[Hard] 6294. 最大价值和与最小价值和的差值

链接: 6294. 最大价值和与最小价值和的差值

1. 题目描述

2. 思路分析

• 比赛时写了一个麻烦的树形DP，先求出每个子树最高和次高、节点深度。然后进行第二次dfs更新答案。
• 赛后抄题解区一个换根DP，思路类似，但更清晰。
• 定义f[i][0/1/2]代表:i向下走最大路径和，向下走次大路径和，向上走最大路径和；答案一定在向下或向上走的路径中.

• 灵神用了更快的解法，一次遍历，类似树的直径那种一次树形DP。
• 由于最大路径和一定存在于某颗子树的两条最大路径上，计算这两条，加起来即可。
• 由于只做了一次dfs，注意用两个变量储存之前查过的，然后用当前更新答案即可。

3. 代码实现

换根DP

class Solution:
    def maxOutput(self, n: int, edges: List[List[int]], price: List[int]) -> int:
        g = [[] for _ in range(n)]
        for u,v in edges:
            g[u].append(v)
            g[v].append(u)
            # print(u,v)
        ans = 0

        f = [[0,0,0] for _ in range(n)]  # f[i][0/1/2]代表:i向下走最大路径和，向下走次大路径和，向上走最大路径和；答案一定在向下或向上走的路径中
        def dfs1(u,fa):  # 更新向下走的最大/次大路径和
            f[u][0] = p = price[u]
            for v in g[u]:
                if v != fa:
                    dfs1(v,u)
                    x = f[v][0]+p
                    if f[u][0]<x:
                        f[u][1] = f[u][0]
                        f[u][0] = x
                    elif f[u][1] < x:
                        f[u][1] = x 
        
        def dfs2(u,fa):
            for v in g[u]:
                if v != fa:
                    p = price[v]
                    if f[u][0] == f[v][0] + price[u]:
                        f[v][2] = max(f[u][2],f[u][1]) + p
                    else:
                        f[v][2] = max(f[u][2],f[u][0]) + p 
                    dfs2(v,u)
        dfs1(0,-1)
        dfs2(0,-1)
                   
        return max(max(a-price[i],c-price[i]) for i,(a,_,c) in enumerate(f))       

树形DP

class Solution:
    def maxOutput(self, n: int, edges: List[List[int]], price: List[int]) -> int:
        g = [[] for _ in range(n)]
        for u,v in edges:
            g[u].append(v)
            g[v].append(u)
            # print(u,v)
        ans = 0

        def dfs(u,fa):
            nonlocal ans
            ms1 = p = price[u]  # 带叶子的最大路径和
            ms2 = 0  # 不带叶子的最大路径和
            for v in g[u]:
                if v != fa:
                    s1,s2 = dfs(v,u)  # 带叶子，不带叶子
                    ans = max(ans,s1+ms2,s2+ms1)  # 当前带叶子的路径和+之前不带叶子的路径和，当前不带叶子+之前带叶子
                    ms1 = max(ms1,s1+p)
                    ms2 = max(ms2,s2+p)
            return ms1,ms2
        dfs(0,-1)
        return ans

六、参考链接