前言

图是一种比线性表和树更为复杂的数据结构。

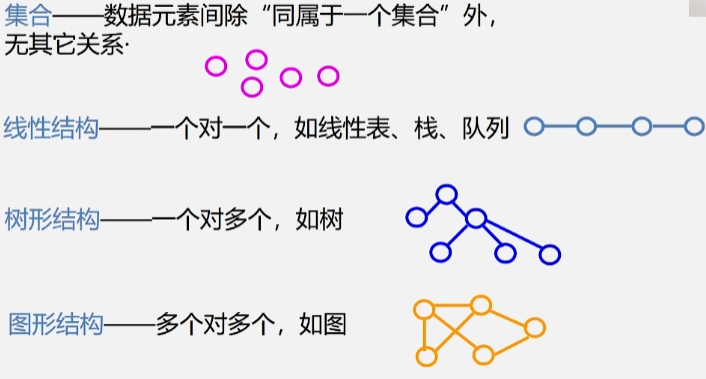
• 在线性结构中，结点之间的关系属于一个对一个；数据元素之间有着线性关系，每个数据元素只有一个直接前趋和一个直接后继，
• 在树形结构中，结点之间的关系属于一个对多个。数据元素之间有着明显的层次关系，并且每一层中的数据元素可能和下一层中的多个元素（即其孩子结点）相关，但只能和上一层中一个元素（即其双亲结点）相关；
• 而在图结构中，结点之间的关系属于多个对多个。结点之间的关系可以是任意的，图中任意两个数据元素之间都可能相关。

6.1 图的定义和术语

1. 图：G = (V,E) —— Graph = (Vertex,Edge)

   • V：顶点（数据元素）的有穷非空结合，一个图当中必须要有顶点；
   • E：边的有穷集合（图里面可以只有点，没有边）。

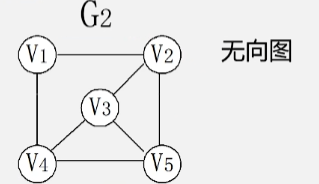
2. 无向图：图中的每条边都是无方向的。

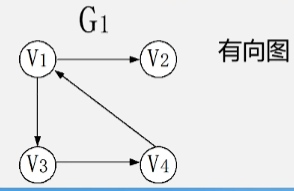
   • G1 这个有向图就是由，V1、V2、V3、V4 这四个顶点，以及四条边组成的，每条边都是有方向的。

3. 有向图：图中的每条边都是有方向的。
   • G2 这个无向图就是由 V1 V2 V3 V4 V5 五个顶点，以及 7 条边构成的，每条边都是无方向的

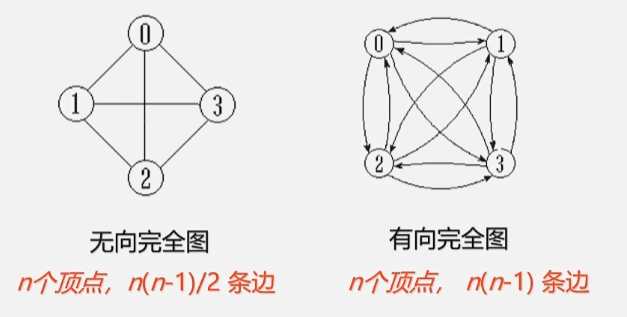
4. 完全图：任意两个顶点都有一条边相连。
   • 无向完全图中：如果有 n 个顶点的话，则必须有 n(n-1)/2 条边。
   • 有向完全图中：如果有 n 个顶点的话，则必须有 n(n-1) 条边。

5. 稀疏图：有很少边或弧的图（e < nlogn，e < 顶点数 X 顶点数的对数）。

   • 弧：有向图那种带箭头的边称作弧，无向图的则称之为边。

6. 稠密图：有较多边或弧的图。

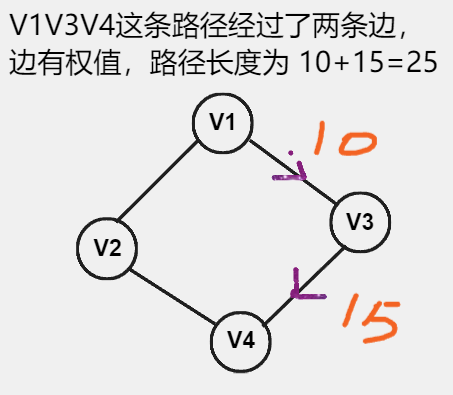
7. 网：边 / 弧 带权的图。

   • 比若说有两个顶点，表示两个地点，这两个地点之间有条路，这条路十公里，这个 十 就是权。
   • 给 边/权 加的这个有特殊意义的值就为权 。
     

8. 邻接：两个顶点之间有 边 / 弧 连在一起，则称为邻接，反之不邻接。

   • 存在（Vi，Vj），则称 Vi 和 Vj 互为邻接点。(Vi，Vj)表示 Vi 到 Vj 之间有一条边。
   • 存在 <Vi，Vj>，则称 Vi 邻接到 Vj，Vj 邻接于 Vi。<Vi，Vj>表示在有向图中存在一条从 VI 到 Vj 的弧。

9. 关联（依附）：边 / 弧 与顶点之间的关系。

   • 存在 (Vi,Vj) / <Vi,Vj>，则称该 边 / 弧 关联于 Vi 和 Vj。

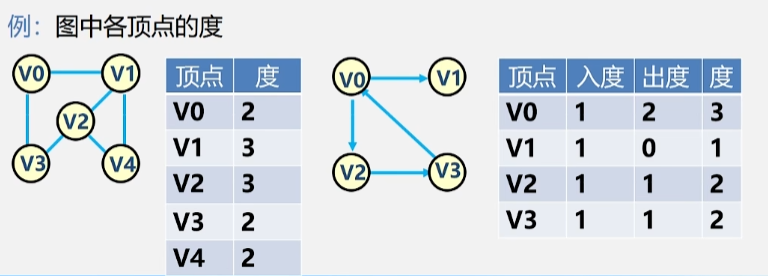
10. 顶点的度：与该顶点向关联的边的数目，记为 TD(v)。

    • 在有向图中，顶点的度等于该顶点的入度与出度之和。
      • 因为有向图的边是有方向的，所以存在入度出度之分。
    • 顶点 V 的入度是以 V 为终点的右向边的条数，记作 ID(V)。
    • 顶点 V 的出度是以 V 为起点的有向边的条数，记作 OD(V)。

这两条边对于 V1 来说，上面的为出度，下面的为入度。

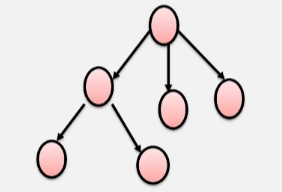
问：当有向图中仅一个顶点的入度为 0，其余顶点的入度均为 1，此时是何形状？
答：是树！而且是一棵有向树！

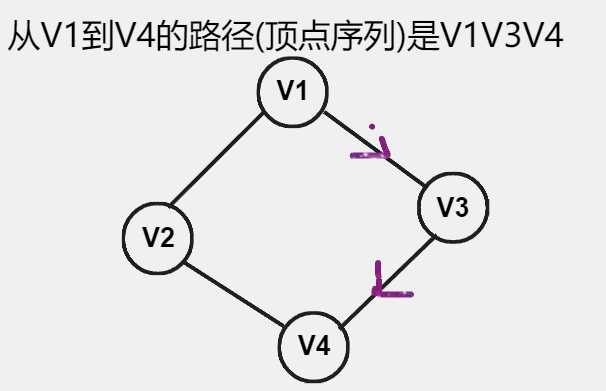
11. 路径：接续的边构成的顶点序列。

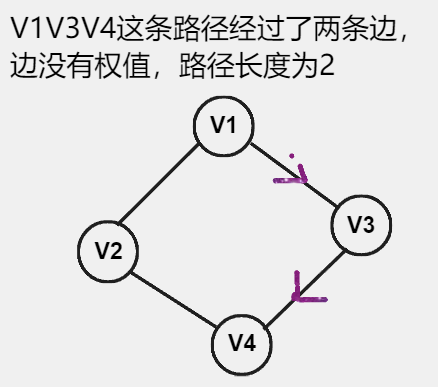
12. 路径长度：路径上 边或弧 的 数目或权值 之和。

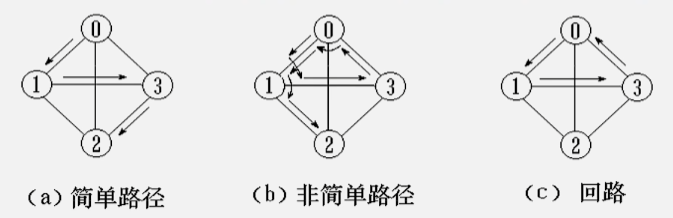
13. 回路（环）：第一个顶点和最后一个顶点的路径是相同的。
14. 简单路径：除了路径起点和路径终点可以相同外，其余顶点均不相同的路径。
15. 简单回路（简单环）：除了起点和终点相同的路径之外，其余顶点均不相同的路径。

16. 连通图（强连通图）：无向图称为连通图，有向图称为强连通图。
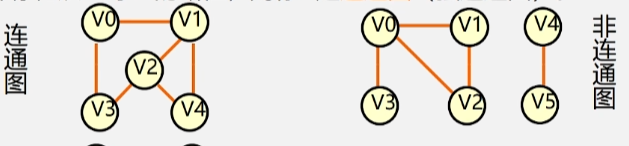
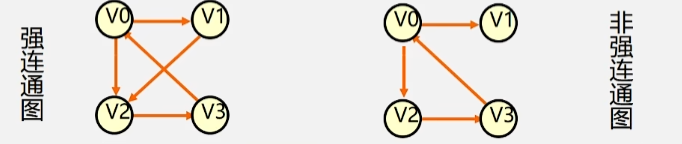
    • 在无（有）向图 G = (V,{E}) 中，若任意两个顶点 v、u 之间都存在从 v 到 u 的路径，则称 G 是 连通图（强连通图）。

随便两个顶点之间都可以找到路径称为连通图，如：从V0到V4,可以走V0V1V4这条路，也可以走V0V3V2V4这条路。非连通图从V0就走不到V5了。

强连通图的每个顶点必然是有出度和如入度的，非强连通图则不是。

17. 权和网

    • 图中 边或弧 所具有的相关数称为权。表明从一个顶点到另一个顶点的距离或耗费。
    • 带权的图称为网。

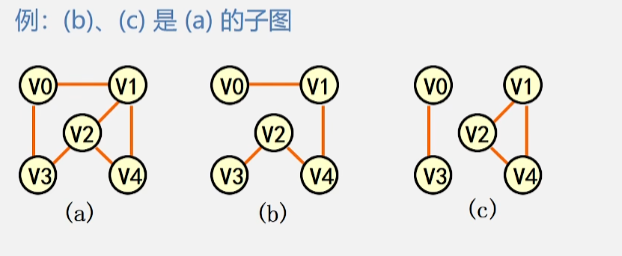
18. 子图

    • 假设有两个图 G = (V,{E})、G1 = (V1,{E1})，若 V1 属于 V，E1 属于 E，则称 G1 是 G 的子图。
    • V 是顶点，E 是边。

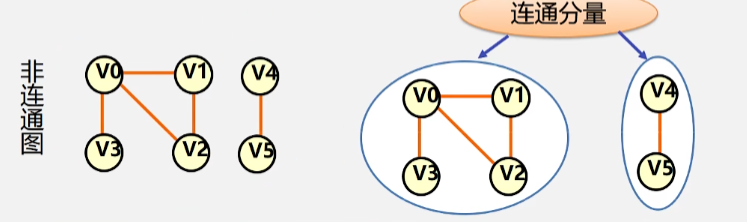
19. 连通分量（强连通分量）
    • 无向图 G 的极大连通子图称为 G 的连通分量。
      • 极大连通子图意思是：顶点的数目在这个子图当中已经达到最大，再加入一个顶点，这个子图就不再是连通图了。
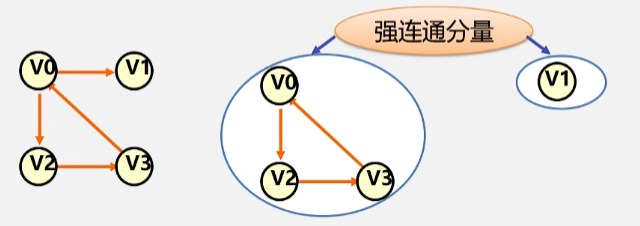
    • 有向图 G 的极大强连通子图称为 G 的墙连通分量。
      • 极大强连通子图的意思是： 顶点数目已经达到最大不能再加了，否则就不再是强连通图了。

在连通分量左边的连通子图中，如果再加入 V4或者V5，都会让左边的连通子图不再连通。

可以将左边的这个非强连通图分成两个连通图。

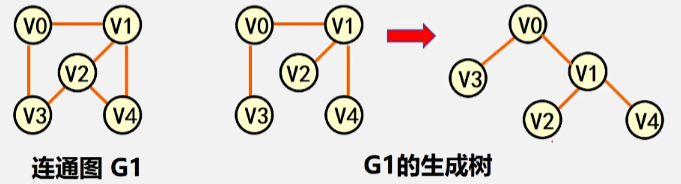
20. 极小连通子图：顶点的数目在这个连通子图中的数目已经达到最小，如果在该图中删除任何一个顶点，则子图不再连通。
21. 生成树：包含无向图 G 所有顶点的极小连通子图。
22. 生成森林：对非连通图，由各个连通分量的生成树的集合。