题目

在英语中，我们有一个叫做 词根(root) 的概念，可以词根后面添加其他一些词组成另一个较长的单词——我们称这个词为 继承词(successor)。例如，词根an，跟随着单词 other(其他)，可以形成新的单词 another(另一个)。
现在，给定一个由许多词根组成的词典 dictionary 和一个用空格分隔单词形成的句子 sentence。你需要将句子中的所有继承词用词根替换掉。如果继承词有许多可以形成它的词根，则用最短的词根替换它。
你需要输出替换之后的句子。

示例 1：

• 输入：dictionary = [“cat”,“bat”,“rat”], sentence = “the cattle was rattled by the battery”
• 输出：“the cat was rat by the bat”

题解

方法1 哈希

该题目写的太晦涩，其实题意很简单，就是对sentence中的每个单词在dictionary中找最短的前缀，如果有就替换，没有不替换。暴力点的做法就是把sentence中的单词逐个的匹配dictionary中的单词，找出最短的前缀。为了加速，比较容易想到的就是用哈希，这里可以对dictionary用哈希集合，也可以用hash表，测试了下hash即可的效率高一些。接下来面临的问题就是如果一个单词匹配多个前缀需要选择最短的一个。这个就通过对word从左遍历，最选匹配到的就是最短的。直接写代码如下：

class Solution:
    def replaceWords(self, dictionary: List[str], sentence: str) -> str:
        dictionarySet = set(dictionary)
        word_list=sentence.split()
        for i, word in enumerate(word_list):
            for j in range(1, len(word) + 1):
                if word[:j] in dictionarySet:
                    word_list[i] = word[:j]
                    break
        return ' '.join(word_list)

计算复杂度

• 时间复杂度。假设d是dictionary的字符数，构建哈希结合的时间复杂度为$O(d)$，假设sentence中一共有m个单词，每个单词的长度为n，则每个单词的前缀是否属于hash即可的判断时间复杂度为$O(n^2)$,因此，整个时间复杂度为$O(d+m\ast n^2)$。
• 空间复杂度。哈希集合的占用空间为$O(d)$，分割setence占用空间为$O(n)$，整体的空间复杂度为$O(d+n)$

方法2 字典树

这道题目首先想到的就是字典树。利用哈希表的方法是在看到官方题解才想到的，因为使用哈希表也存在大量的重复比较。因此字典树才是这道题目的核心考核点。首先，需要根据dictionary构建字典树，因此字典树的类需要一个构建功能。其次需要一个搜索字符的功能，这个功能与典型的字典树稍微有区别，这里只需要匹配到最短的一个树，而不需要匹配完整个字符串，在找最短前缀字典树占优势，碰到第一个终止的字符时结束返回这个字符串即可。为了方便可以增加一个prefix变量用来存储每个字典树的根节点到结束字符之间的字符串，这个字符串就是搜索字符串的前缀，方便直接输出结果。
以示例1为例给出字典树的数据结构图：

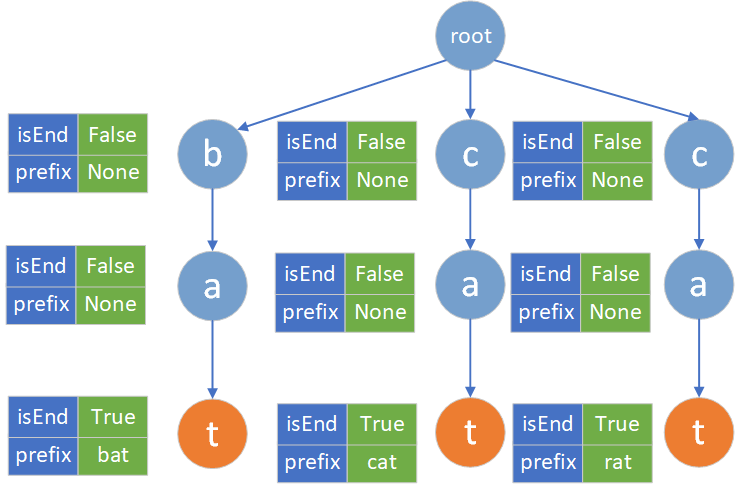
字典树的构建跟典型字典树差别不大，只需增加一个prefix变量即可。而搜索需要有所修改，在碰到第一个isEnd为True有节点也就是橘黄色节点时，需要返回该节点prefix节点值，如果没有匹配上返回空。
代码：

class Trie:
    def __init__(self):
        self.children=[None]*26
        self.isEnd=False
        self.prefix=None


    def insert(self,word):
        node=self
        for ch in word:
            num=ord(ch)-ord("a")
            if not node.children[num]:
                #创建节点
                node.children[num]=Trie()
            node=node.children[num]
        node.isEnd=True
        node.prefix=word

    
    #搜索最短前缀
    def prefix_search(self,word):
        node=self
        for ch in word:
            num=ord(ch)-ord("a")
            if node.children[num]:
                if node.children[num].isEnd:
                    return node.children[num].prefix
                node=node.children[num]
            else:
                return ''
            
class Solution:
    def replaceWords(self, dictionary: List[str], sentence: str) -> str:
        dict_tree=Trie()
        #建立词根的字典序
        for word in dictionary:
            dict_tree.insert(word)
        sen_list=sentence.split()
        for i in range(len(sen_list)):
            if dict_tree.prefix_search(sen_list[i]):
                sen_list[i]=dict_tree.prefix_search(sen_list[i])
        return ' '.join(sen_list)

官方代码理解

官方代码更简介一些，主要是采用了嵌套dict来实现字典树。示例1中的dictionary构建的字典树如下图所示：

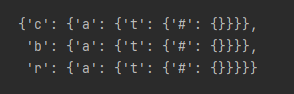
官方代码如下：

class Solution:
    def replaceWords(self, dictionary: List[str], sentence: str) -> str:
        #利用嵌套字典构建字典树
        trie = {}
        for word in dictionary:
            cur = trie
            for c in word:
                if c not in cur:
                    cur[c] = {}
                cur = cur[c]
            # #号作为一个word的终止符
            cur['#'] = {}

        words = sentence.split(' ')
        for i, word in enumerate(words):
            cur = trie
            for j, c in enumerate(word):
                #碰到的第一个终止符直接替换，跳出循环，因为第一个是最小前缀
                if '#' in cur:
                    words[i] = word[:j]
                    break
                if c not in cur:
                    break
                cur = cur[c]
        return ' '.join(words)

整体来说如果对字典树比较熟悉，通过第一种方法构建字典树这种方法虽然代码长，但是思路比较清晰。第二种构建字典树的方法简洁，很有技巧性。

计算复杂度

• 时间复杂度。构建字典树消耗 $O(d)$ 时间，字典数的搜索的复杂度为$O(1)$，因此整体的时间复度为$O(d)$。
• 空间复杂度。哈希集合的占用空间为$O(d)$，分割setence占用空间为$O(n)$，整体的空间复杂度为$O(d+n)$