当前位置：首页 > news >正文

算法第十二期——BFS-双向广搜

news 来源：原创 2024/11/13 13:20:58

双向广搜

应用场景：有确定的起点s和终点t；把从起点到终点的单向搜索，变换为分别从起点出发和从终点出发的“相遇”问题。
操作：从起点s(正向搜索）和终点t(逆向搜索）同时开始搜索，当两个搜索产生相同的一个子状态v时就结束，v是相遇点。得到的s-v-t是一条最佳路径。
队列：一般用两个队列分别处理正向BFS和逆向BFS。

双向广搜的复杂度

当下一层扩展的状态很多时，双向广搜能大大优化，减少大量搜索。
图（1）单个BFS搜索到第四层需要搜索1+2+4+8+16=32次，二图（2）双向BFS只需要1+2+4+2+1=10次，显然效率更高。

注意：双向广搜对二叉树有很大的优化，但对网格图并没有很好的效果。

例题：跳蚱蜢

跳蚱蜢2017年第八届省赛，lanqiao0J题号642

【题目描述】

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

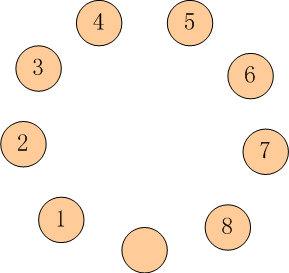
如下图所示：有 9 只盘子，排成 1 个圆圈。其中 8 只盘子内装着 8 只蚱蜢，有一个是空盘。我们把这些蚱蜢顺时针编号为 1 ~ 8。

每只蚱蜢都可以跳到相邻的空盘中，也可以再用点力，越过一个相邻的蚱蜢跳到空盘中。

请你计算一下，如果要使得蚱蜢们的队形改为按照逆时针排列，并且保持空盘的位置不变（也就是 1−8 换位，2−7换位,...），至少要经过多少次跳跃？

【思路】

队列q1:正向搜索

队列q2:逆向搜索
由于起点和终点的串不同，正向BFS和逆向BFS扩展的下一层数量也不同，也就是进入2个队列的串的数量不同，先处理较小的队列，可以加快搜索速度。

建模

直接让蚱蜢跳到空盘有点麻烦，因为有很多在跳蚱蜢。
每一次跳跃有一只蚱蜢跳到空盘，如果我们反过来看，让空盘跳，跳到蚱蜢的位置，简单多了，每个队列只有一个空盘在跳。

化圆为线

题目是一个圆圈，不好处理，用一个建模技巧“化圆为线”，把圆形转换为线形。
把空盘看成0，有9个数字{0,1,2,3,4,5,6,7,8}，一个圆圈上的9个数字，拉直成了一条线上的9个数字，这条线的首尾两个数字0和8处理成相连的。
八数码问题:有9个数字{0,1,2,3,4,5,6,7,8}，共有9!=362880种排列（10w种），不算多。

最短路径

用BFS扩展每一层，每一层就是蚱蜢（建模成‘’空盘‘’）跳了一次。
初始状态（队列1）:“012345678”，目标状态（队列2）:“087654321”。
从初始状态“012345678”跳一次，有4种情况:0跳到1（向右跳一个），2（向右跳两个）,7（向左跳一个）,8（向左跳两个）这几个点，即“1023456783"、“210345678”、“812345670”、“712345608"，等价于交换了空盘编号0和空盘跳到的蚂蚱编号。同样的，从目标状态“087654321”跳一次也是4这种情况。
然后从这4种状态继续跳到下一种状态，一直跳到目标状态为止，队列1的状态第一次出现在队列2中就是出现了最短路径，记录步数：正向搜索步数+当前这一步+逆向搜索步数。

【代码】

from queue import *
cnt = 0
meet = False
def extend(q,m1,m2):
    global cnt
    global meet
    s = q.get() # 弹出队首状态
    for i in range (len(s) ):   # 找出该状态下0的位置
        if s[i]=='0': break
    for j in range(4): # 四种跳的情况：左1，左2，右1，右2
        cnt += 1            #统计计算次数
        news = list(s)      # 把字符串转成list，后面方便处理
        # 化圆为方
        if j==0: news[(i-2+9)%9] ,news[i] = news[i], news[(i-2+9)%9] # 往左跳1个，把跳到的数与0交换
        if j==1: news[(i-1+9)%9], news[i] = news[i], news[(i-1+9)%9] # 往左跳2个
        if j==2: news[(i+1+9)%9], news[i] = news[i], news[(i+1+9)%9] # 往右跳1个
        if j==3: news[(i+2+9)%9], news[i] = news[i], news[(i+2+9)%9] # 往右跳2个
        a = "".join(news)   # 处理完再转回字符串重新转成字符串
        if a in m2:         # 结束条件:第一次相遇(队列1的状态在队列2里出现过)，就是最短路径
            print(m1[s] + 1 + m2[a])    # 正向搜索的步数+当前这一步+逆向搜索的步数
            # print(cnt)    # 打印计算次数：54560
            meet = True
            return
        if a not in m1:     # 若该状态不在队列1
            q. put(a)       # 加入队列
            m1[a] = m1[s]+1        # 向字典中添加状态和当前步数
    meet = False
q1 = Queue()  # 正向搜索
q2 = Queue()  # 逆向搜索
q1.put("012345678")
q2.put("087654321")
mp1={'012345678':0}   # 定义字典（用于判重）：状态，当前步数
mp2={'087654321':0}
while not q1.empty() and not q2.empty(): # 两个队列都不为空
    if q1.qsize() <= q2.qsize() : extend(q1, mp1, mp2) # 若队列1较小，先处理队列1
    else:                         extend(q2, mp2, mp1) # 若队列2较小，先处理队列2
    if meet==True: break    # 相遇就结束

计算量：