【算法基础】1.6 双指针算法
文章目录
- 双指针思想
- 最长连续不重复子序列
- 数组元素的目标和
- 题目
- 讲解
- 判断子序列
双指针思想
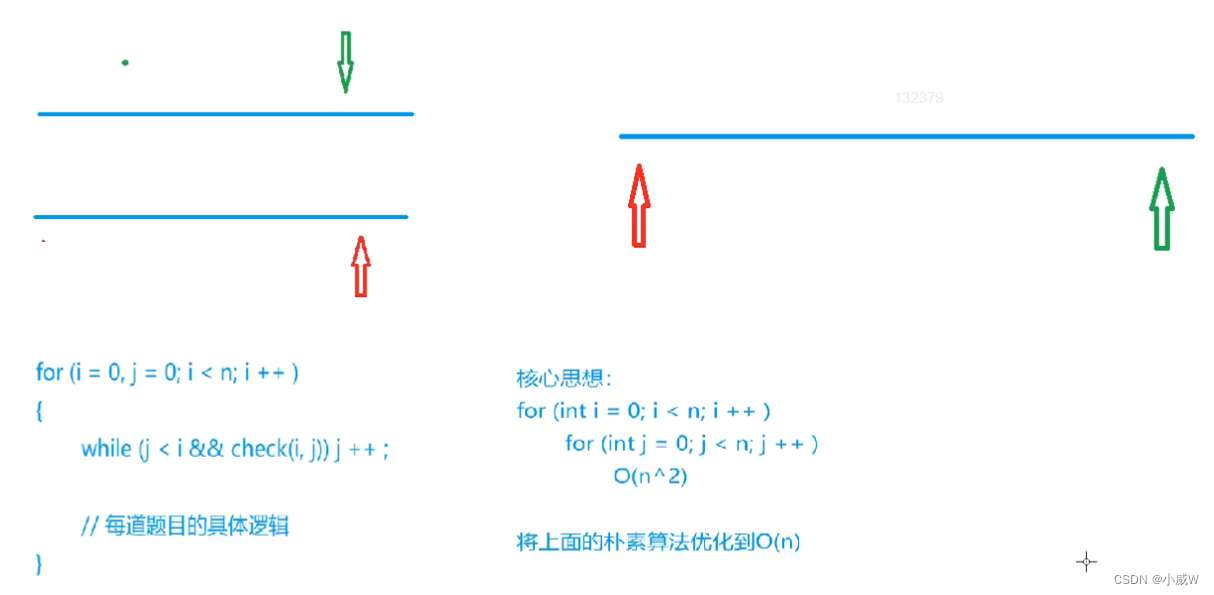
双指针算法,就是可以将 n ^ 2 优化到 n。
最长连续不重复子序列
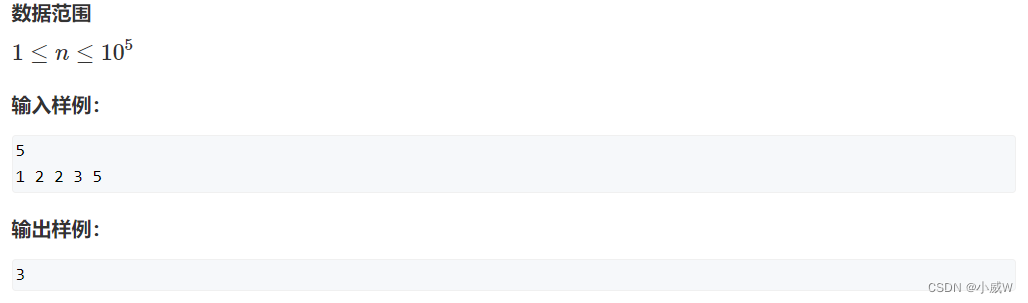
给定一个长度为 n 的整数序列,请找出最长的不包含重复的数的连续区间,输出它的长度。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 5;
int a[N], cnt[N];
int main()
{
int n, ans = 0;
scanf("%d", &n);
for (int i = 0, j = 0; i < n; ++i) {
scanf("%d", &a[i]);
++cnt[a[i]];
while (cnt[a[i]] > 1) --cnt[a[j++]];
ans = max(ans, i - j + 1);
}
printf("%d\n", ans);
return 0;
}
相似题目:
https://leetcode.cn/problems/longest-substring-without-repeating-characters/
https://leetcode.cn/problems/zui-chang-bu-han-zhong-fu-zi-fu-de-zi-zi-fu-chuan-lcof/
数组元素的目标和
题目
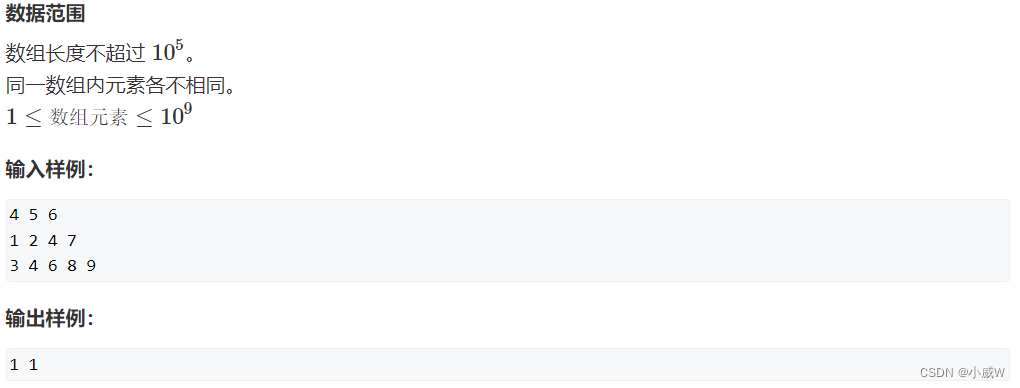
给定两个升序排序的有序数组 A 和 B,以及一个目标值 x。
数组下标从 0 开始。
请你求出满足 A[i]+B[j]=x 的数对 (i,j)。
数据保证有唯一解。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int main()
{
int n, m, x;
scanf("%d%d%d", &n, &m, &x);
int a[n], b[m];
for (int i = 0; i < n; ++i) scanf("%d", &a[i]);
for (int i = 0; i < m; ++i) scanf("%d", &b[i]);
for (int i = 0, j = m - 1; i < n && j >= 0;) {
if (a[i] + b[j] == x) {
printf("%d %d\n", i, j);
break;
} else if (a[i] + b[j] < x) ++i;
else --j;
}
return 0;
}
讲解
这道题的关键是想到一个数组从前往后,另一个数组从后往前。
这里是两个数组,如果是一个数组的话也是一样的。
这样处理可以保证一个指针一直往前,另一个指针一直往后,它们的移动方向是不变的。
判断子序列
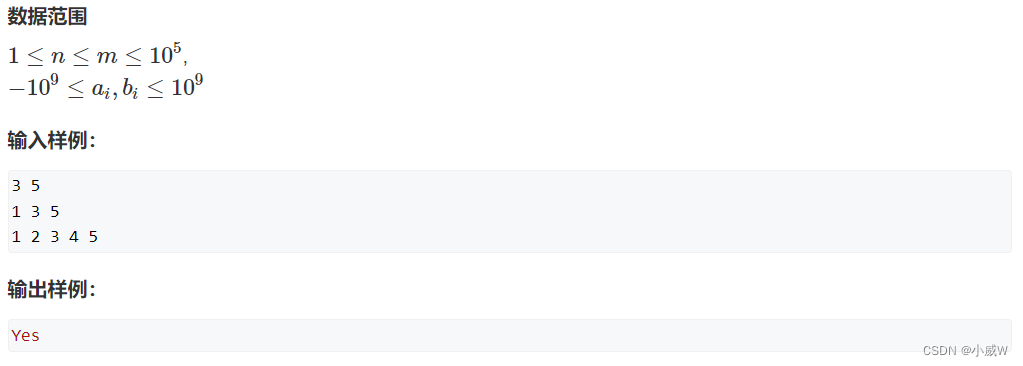
给定一个长度为 n 的整数序列 a1,a2,…,an 以及一个长度为 m 的整数序列 b1,b2,…,bm。
请你判断 a 序列是否为 b 序列的子序列。
子序列指序列的一部分项按原有次序排列而得的序列,例如序列 {a1,a3,a5} 是序列 {a1,a2,a3,a4,a5} 的一个子序列。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int main()
{
int n, m;
scanf("%d%d", &n, &m);
int a[n], b[m];
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
for (int i = 0; i < m; i ++ ) scanf("%d", &b[i]);
int i = 0, j = 0;
for (; i < m && j < n; ++i) {
if (a[j] == b[i]) ++j;
}
if (j == n) puts("Yes");
else puts("No");
return 0;
}
这个思路就很简单了,两个指针分别去遍历两个数组,相同时才移动需要匹配的数组,这样到最后如果走过了完整一遍,说明就匹配到了。
