导航算法

本节详细介绍导航算法。

ISAAC教程合集地址: https://blog.csdn.net/kunhe0512/category_12163211.html

全局路径规划器

Isaac 框架中的全局规划器问题被分解为三类：规划器模型、可见性图算法和优化器。

规划器模型

规划器模型 (sdk/packages/path_planner/gems/planner_model.hpp) 必须提供以下内容：

• 一组函数，提供有关给定状态是否无碰撞的信息。

• 有关两个状态之间是否存在直接路径（简单路径，例如直线）且无碰撞的信息。

• 路径的距离或长度。

• 一种在状态空间中随机采样的方法。

在carter平台的情况下，差分基座近似为圆形，允许使用距离图进行快速碰撞检测。 直接路径定义为直线上的短路径 (< 2m)（因为我们始终可以沿该方向旋转）。 因此规划问题是一个二维问题。

可见性图算法

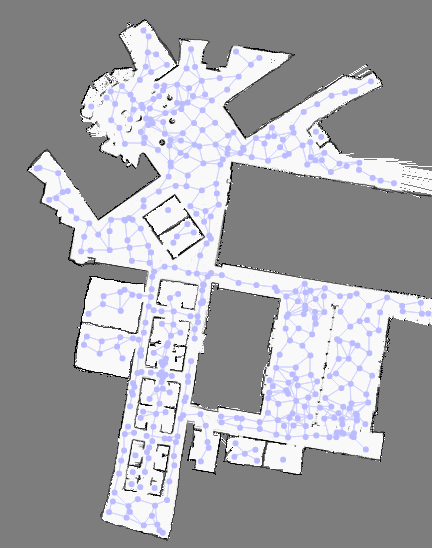
灵感来自 T. SIMÉON, J.-P. LAUMOND和 C. NISSOUX 的论文“基于可见性的运动规划概率路线图”，可见性图算法提供了一种非常通用的算法来在高维空间中寻找路径。 目标是生成一个具有高可见性覆盖率的小图。

该图是通过保留一组不能直接相互连接的点（在论文中称为守卫）来构建的。 只要存在直接连接未通过任何路径连接的两个守卫的中间状态，就会添加连接。

Isaac 实现在未通过大小为 2 的路径连接的守卫之间添加了一个连接，仅使用一个中间状态。 这会产生更大但质量更高的图表。

一旦构建了图形，就可以通过首先找到这些状态与守卫之间的连接，然后在图形上运行 Djikstra 算法来计算最短路径。 只要环境是静态的，就可以预先计算同一个图，在遇到困难问题时手动辅助，并重复用于其他最短路径请求。

为了获得更好的性能，请通过增加随机样本的数量来构建密集图。

优化器

最终状态是路径优化。 快速路径生成期间的可见性图会产生非常混乱的路径。 然后使用捷径计算质量更好的路径：随机选择两个路径点，如果它们之间存在直接路径，则绕过中间的所有路径点。 此外，接近障碍物的航路点从最近的障碍物移开。

轨迹规划器

Isaac 的局部规划器是基于线性二次调节器 (LQR) 的。 Isaac SDK 提供可定制的 LQR 求解器。 系统的动力学以及成本函数需要提供给 LQR 求解器，后者使用线性搜索执行迭代梯度下降以找到最佳路径。

在carter 平台的情况下，系统的动态是微分基础的动态：

• State:

  • $x(t)$: X position of the base

  • $y(t)$: Y position of the base

  • $\theta (t)$: Orientation of the base

  • $v(t)$: Linear velocity

  • $\theta \prime (t)$: Angular velocity

• Control:

  • $al(t)$: Left wheel angular acceleration

  • $ar(t)$: Right wheel angular acceleration

动力学然后由公式给出（L 是基本长度，R 是车轮半径）：

• $x\prime (t)=v(t)cos(\theta (t))$

• $y\prime (t)=v(t)sin(\theta (t))$

• $\theta \prime (t)=\theta \prime (t)$

• $v\prime (t)=a(t)=(ar(t)+al(t))\cdot R/2$

• $\theta \prime \prime (t)=(ar(t)-al(t))\cdot R/L$

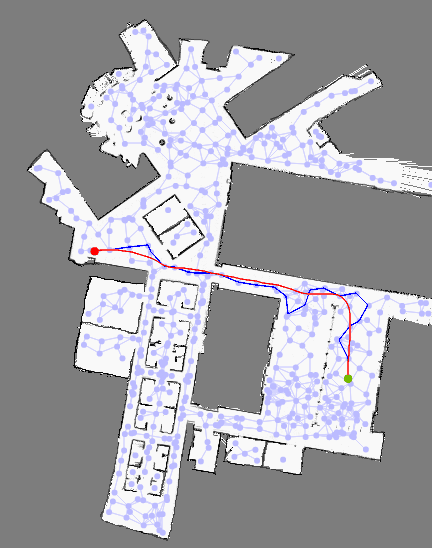
以下是 carter 在本地视图中生成的路径示例：

本地地图和距离地图都是实时计算的。 红色是全局规划器提供的路径，蓝色是 LQR 生成的计划，优化速度、障碍物距离、加速度和其他因素。

更多精彩内容:
https://www.nvidia.cn/gtc-global/?ncid=ref-dev-876561