力扣 221. 最大正方形
目录
第一站 LeetCode 新手村
前言
1480. 一维数组的动态和221. 最大正方形1480. 一维数组的动态和
题目描述
解题思路
代码
总结
题目来源
第一站 LeetCode 新手村
前言
最近玩OJ赛,发现对算法的理解还需要更加扎实,code能力还可以进一步提升,所以做这样一个算法的系列文章,用于记录学习心得,交流经验,更好地进步和成长。
221. 最大正方形
题目描述
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
示例1
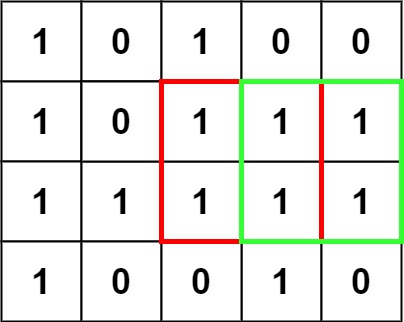
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:4
示例 2
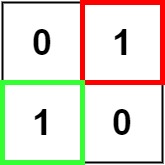
输入:matrix = [["0","1"],["1","0"]] 输出:1
示例 3
输入:matrix = [["0"]] 输出:0
提示
-
m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 '0' 或 '1'
解题思路
预知
LeetCode是核心代码模式,所以只需要考虑核心算法,输入由系统自动完成,最后的输出以return返回;
思路
动态规划
代码
C++
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if(matrix.size()==0 || matrix[0].size()==0){ //特殊情况的判断,若数组为空,或数组不为空,但其内容为空,返回0
return 0;
}
int maxSide = 0; //定义最大边,该图像是正方形,最后返回边的平方即可
int rows = matrix.size(), columns = matrix[0].size();
vector<vector<int>> dp(rows, vector<int>(columns)); //初始化包含row个vector<int>(columns)容器的vector容器 其实就是创建了一个和题目所给数据同样大小的二维数组
for(int i=0;i<rows;i++){ //按行遍历数组
for(int j=0;j<columns;j++){ //进入行遍历某一行的某个元素
if(matrix[i][j]=='1'){ //当元素为1时开始记录
if(i==0 || j==0){ //如果是第一行或者是第一列
dp[i][j]=1; //直接给该元素赋值
}else{
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
//访问该元素上方和左侧,和左上侧对角元素
//dp[i][j]代表右下角 而记录在dp[i][j]中的数就是最大边长
//正方形套正方形,若想构成一个边长为3的正方形其必经过3个边长为2的正方形
}
maxSide = max(maxSide, dp[i][j]); //比较dp值并返回最大边长
}
}
}
int maxSquare = maxSide * maxSide; //正方形面积
return maxSquare;
}
};总结
以上就是今天要讲的内容,本文仅仅简单讲解了《最大正方形》这一题目,并对动态规划有了进一步的了解
l题目来源
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/maximal-square
